Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:55:49.542Z Has data issue: false hasContentIssue false
  • English
  • Français

On some fractional integrals and their applications

Published online by Cambridge University Press:  20 January 2009

J. S. Lowndes
J. S. Lowndes
Affiliation:
Department of MathematicsUniversity of StrathclydeGlasgow G1 1XH
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In previous papers [3, 4] the author has discussed the symmetric generalised Erdélyi–Kober operators of fractional integration defined by

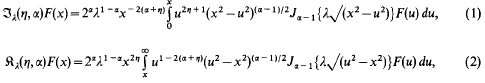
where α>0, γ≧0 and the operators ℑiγ(η,α) and 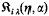defined as in equations (1) and (2) respectively but with Jα−1, the Bessel function of the first kind replaced by Iα−1, the modified Bessel function of the first kind.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 28 , Issue 1 , February 1985 , pp. 97 - 105
Copyright
Copyright © Edinburgh Mathematical Society 1985

References

REFERENCES

1.Gilbert, R. P., Function theoretic methods in partial differential equations (Academic Press, 1969).Google Scholar
2.Lowndes, J. S., Parseval relations for Kontorovich-Lebedev transforms, Proc. Edinburgh Math.Soc. 13 (1962), 5–11.CrossRefGoogle Scholar
3.Lowndes, J. S., A generalisation of the Erdélyi–Kober operators, Proc. Edinburgh Math. Soc. 17 (1970), 139–148.CrossRefGoogle Scholar
4.Lowndes, J. S., An application of some fractional integrals, Glasgow Math. J. 20 (1979), 35–41.CrossRefGoogle Scholar
5.Magnus, W., Oberhettinger, F. and Soni, R. P., Formulas and theorems for the special functions of mathematical physics, 3rd ed. (Springer-Verlag, 1966).CrossRefGoogle Scholar
6.Vekua, I. N., New methods for solving elliptic equations (North-Holland, 1967).Google Scholar