Published online by Cambridge University Press: 20 January 2009
A few definite integrals involving more than two Legendre functions in the integrand have been considered by Ferrers, Adams, Dougall, Nicholson and Bailey. We take for example the following integrals.
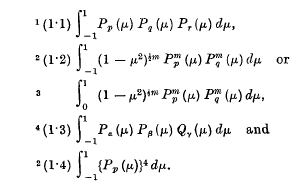
page 41 note 1 Hobson, Spherical and Ellipsoidal Harmonics, p. 87. The references to Ferrers and Adams, who considered this integral, are given there.Google Scholar
page 41 note 2 Bailey, W. N. “On the product of two Legendre functions,” Proc. Camb. Phil.Soc. 29 (1933), 173, results (4·1) and (4·2).CrossRefGoogle Scholar
page 41 note 3 Dougall, J., Proc. Edin. Math. Soc. 37 (1919), 33–47, formula (3).CrossRefGoogle Scholar
page 41 note 4 Nicholson, Phil. Mag. (6) 43 (1922), 783.Google Scholar
page 41 note 5 Phil. Mag. (6), 43 (1922), 1–29,“Zonal Harmonics of the second kind.”CrossRefGoogle Scholar
page 42 note 1 L.c., formula (5·4).
page 42 note 2 I have to thank a referee for suggesting this notation and other modifications in this paper.
page 42 note 3 Prasad, Ganesh, “On non-orthogonal systems of Legendre's functions,” Proc. Benares Math. Soc., 12 (1930), 33–42.Google Scholar
page 42 note 4 Shabde, “On some series and integrals involving Legendre functions,” Bull. Calcutta Math. Soc., 25 (1933), 29.Google Scholar
page 43 note 1 Dhar, and Shabde, , “On the non-orthogonality of Legendre's functions,” Bull. Calcutta Math. Soc., 24 (1932), 185.Google Scholar
page 44 note 1 Prasad, Ganesh, l.c., p. 40.Google Scholar
page 44 note 2 Bailey, W. N., l.c., formula (3·3).Google Scholar
page 45 note 1 Sirkar, H. K., Proc. Edtn. Math. Soc., 2, 1 (1927–1929), 244, “On the evaluation of ![]() and
and ![]() .”Google Scholar
.”Google Scholar
page 46 note 1 L.c., p. 38.
page 46 note 2 Phil. Mag. (6), 43 (1922), 1–29.CrossRefGoogle Scholar