Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Jurkat, W. B.
and
Troutman, J. L.
1979.
Maximal inequalities related to generalized a.e. continuity.
Transactions of the American Mathematical Society,
Vol. 252,
Issue. 0,
p.
49.
Chvátal, V.
and
Szemerédi, E.
1982.
On an Extremal Problem Concerning Intervals.
European Journal of Combinatorics,
Vol. 3,
Issue. 3,
p.
215.


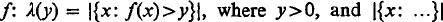 denotes the Lebesgue measure of the set specified. We shall suppose that λ(
denotes the Lebesgue measure of the set specified. We shall suppose that λ(