Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-10T21:00:44.388Z Has data issue: false hasContentIssue false
  • English
  • Français

On non-separated zero sequences of solutions of a linear differential equation

Part of: Spaces and algebras of analytic functions Function theory on the disc Qualitative theory Geometric function theory

Published online by Cambridge University Press:  30 April 2021

Igor Chyzhykov  and
Jianren Long
Igor Chyzhykov
Affiliation:
Faculty of Mechanics and Mathematics, Lviv Ivan Franko National University, Universytets'ka 1, 79000Lviv, Ukraine ([email protected])
Jianren Long
Affiliation:
School of Mathematical Sciences, Guizhou Normal University, Guiyang, 550025, Guizhou, China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $(z_k)$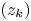 be a sequence of distinct points in the unit disc $\mathbb {D}$ 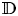without limit points there. We are looking for a function $a(z)$ 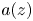analytic in $\mathbb {D}$ 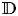and such that possesses a solution having zeros precisely at the points $z_k$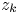, and the resulting function $a(z)$ 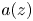has ‘minimal’ growth. We focus on the case of non-separated sequences $(z_k)$ 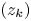in terms of the pseudohyperbolic distance when the coefficient $a(z)$ 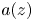is of zero order, but $\sup _{z\in {\mathbb D}}(1-|z|)^p|a(z)| = + \infty$ 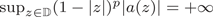for any $p > 0$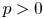. We established a new estimate for the maximum modulus of $a(z)$ 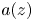in terms of the functions $n_z(t)=\sum \nolimits _{|z_k-z|\le t} 1$ 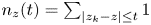and $N_z(r) = \int_0^r {{(n_z(t)-1)}^ + } /t{\rm d}t.$ 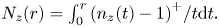The estimate is sharp in some sense. The main result relies on a new interpolation theorem.

Keywords

interpolationunit discanalytic functionoscillation of solutiondifferential equationprescribed zeros

MSC classification

Primary: 34C10: Oscillation theory, zeros, disconjugacy and comparison theory
Secondary: 30C15: Zeros of polynomials, rational functions, and other analytic functions (e.g. zeros of functions with bounded Dirichlet integral) 30H99: None of the above, but in this section 30J99: None of the above, but in this section
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 64 , Issue 2 , May 2021 , pp. 247 - 261
Check for updates
Copyright
Copyright © The Author(s) 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berenstein, C. A. and Taylor, B. A., A new look at interpolation theory for entire functions of one variable, Adv. Math. 33 (1979), 109–143.10.1016/S0001-8708(79)80002-XCrossRefGoogle Scholar
Borichev, A., Dhuez, R. and Kellay, K., Sampling and interpolation in large Bergman and Fock space, J. Funct. Analysis 242 (2007), 563–606.10.1016/j.jfa.2006.09.002CrossRefGoogle Scholar
Chyzhykov, I. and Sheparovych, I., Interpolation of analytic functions of moderate growth in the unit disc and zeros of solutions of a linear differential equation, J. Math. Anal. Appl. 414 (2014), 319–333.10.1016/j.jmaa.2013.12.066CrossRefGoogle Scholar
Chyzhykov, I., Gundersen, G. and Heittokangas, J., Linear differential equations and logarithmic derivative estimates, Proc. London Math. Soc. 86(3) (2003), 735–754.10.1112/S0024611502013965CrossRefGoogle Scholar
Chyzhykov, I., Heittokangas, J. and Rättyä, J., On the finiteness of $\varphi$-order of solutions of linear differential equations in the unit disc, J. d'Analyse Math. 109(1) (2010), 163–196.10.1007/s11854-009-0030-3CrossRefGoogle Scholar
Chyzhykov, I., Heittokangas, J. and Rättyä, J., Sharp logarithmic derivative estimates with applications to ODE's in the unit disc, J. Australian Math. Soc. 88 (2010), 145–167.10.1017/S1446788710000029CrossRefGoogle Scholar
Drasin, D. and Shea, D., Pólya peaks and the oscillation of positive functions, Proc. Amer. Math. Soc. 34 (1972), 403–411.Google Scholar
Gröhn, J., Solutions of complex differential equation having pre-given zeros in the unit disc, Constr. Approx. 49 (2019), 295–306.CrossRefGoogle Scholar
Gröhn, J. and Heittokangas, J., New findings on Bank-Sauer approach in oscillatory theory, Constr. Approx. 35 (2012), 345–361.CrossRefGoogle Scholar
Gröhn, J., Nikolau, A. and Rättyä, J., Mean growth and geometric zero distribution of solutions of linear differential equations, J. Anal. Math. 134 (2018), 747–768.10.1007/s11854-018-0024-0CrossRefGoogle Scholar
Hartmann, A. and Massaneda, X., Interpolating sequences for holomorphic functions of restricted growth, Ill. J. Math. 46(3) (2002), 929–945.Google Scholar
Heittokangas, J., A survey on Blaschke-oscillatory differential equations, with updates, in Blaschke products and their applications (eds J. Mashreghi, E. Fricain), pp. 43–98, Fields Institute Communications, Volume 65, (The Fields Institute for Research in Mathematical Sciences, Springer, Toronto, 2012).CrossRefGoogle Scholar
Heittokangas, J., Solutions of $f''+A(z)f=0$ in the unit disc having Blaschke sequence as zeros, Comp. Meth. Funct. Theory 5(1) (2005), 49–63.CrossRefGoogle Scholar
Levin, B. Ja, Distribution of zeros of entire functions, revised edition, Transl. Math. Monographs, Volume 5, translated by R. P. Boas et al. , Amer. Math. Soc. (Providence, 1980).Google Scholar
Šeda, V., On some properties of solutions of the differential equation $y''=Q(z)y$, where $Q(z)\ne 0$ is an entire function, Acta. Fac. Nat. Univ. Comenian Math. 4 (1959), 223–253, (in Slovak).Google Scholar
Seip, K., Beurling type density theorems in the unit disc, Invent. Math. 113 (1993), 21–39.10.1007/BF01244300CrossRefGoogle Scholar
Vynnyts'kyi, B. and Shavala, O., Remarks on Šeda theorem, Acta. Math. Univ. Comenianae LXXXI(1) (2012), 55–60.Google Scholar