Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T18:54:01.116Z Has data issue: false hasContentIssue false
  • English
  • Français

On meromorphic solutions of functional-differential equations

Part of: Entire and meromorphic functions, and related topics Functional-differential and differential-difference equations

Published online by Cambridge University Press:  10 February 2022

Feng Lü
Feng Lü*
Affiliation:
College of Science, China University of Petroleum, Qingdao, Shandong266580, P.R. China ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider meromorphic solutions of functional-differential equations

\[ f^{(k)}(z)=a(f^{n}\circ g)(z)+bf(z)+c, \]
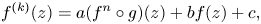
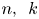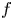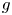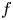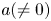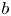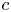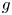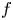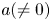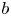where $n,\,~k$ are two positive integers. Firstly, using an elementary method, we describe the forms of $f$ and $g$ when $f$ is rational and $a(\neq 0)$, $b$, $c$ are constants. In addition, by employing Nevanlinna theory, we show that $g$ must be linear when $f$ is transcendental and $a(\neq 0)$, $b$, $c$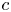 are polynomials in $\mathbb {C}$.

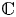Keywords

functional-differential equationmeromorphic solutioncompositiongrowth

MSC classification

Primary: 30D30: Meromorphic functions, general theory 30D35: Distribution of values, Nevanlinna theory
Secondary: 34K06: Linear functional-differential equations
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 263 - 278
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bellman, R. and Cooke, K. L., Differential-difference equations (Academic Press, New York, 1963).Google Scholar
Clunie, J., The composition of entire and meromorphic functions, Mathematical Essays Dedicated to A. J. MacIntyre (Ohio University Press, 1970).Google Scholar
Doeringer, W., Exceptional values of differential polynomials, Pacific J. Math. 98 (1882), 55–62.CrossRefGoogle Scholar
Goldstein, R., On meromorphic solutions of certain functional equations, Aequationes Math. 17 (1978), 116–118.CrossRefGoogle Scholar
Gross, F., On a remark by Utz, Am. Math. Monthly 74 (1967), 1107–1109.CrossRefGoogle Scholar
Gross, F. and Yang, C. C., On meromorphic solution of a certain class of functional-differential equations, Annal. Polonici Math. 27 (1973), 305–311.CrossRefGoogle Scholar
Laine, I., Nevanlinna theory and complex differential equations, Studies in Math. Volume 15 (de Gruyter, Berlin, 1993).CrossRefGoogle Scholar
Li, B. Q. and Saleeby, E. G., On solutions of functional-differential equations $f'(x)=a(x)f(g(x))+b(x)f(x)+c(x)$ in the large, Israel J. Math. 162 (2007), 335–348.Google Scholar
Montel, P., Lecons sur les families normales de functions analytique et leurs applications, (Gauthier-Villars, Paris, 1927).Google Scholar
Oberg, R. J., On the local existence of solutions of certain functional-differential equations, Proc. Am. Math. Soc. 20 (1969), 295–302.CrossRefGoogle Scholar
Oberg, R. J., Local theory of complex functional differential equations, Trans. Am. Math. Soc. 161 (1971), 269–281.CrossRefGoogle Scholar
Ockendon, J. R. and Taylor, A. B., The dynamics of a current collection system for an electric locomotive, Proc. R. Soc. London, Seri. A. 322 (1971), 447–468.Google Scholar
Siu, Y. T., On the solution of the equation $f'(x)=\lambda f(g(x))$, Math Z. 90 (1965), 391–392.CrossRefGoogle Scholar
Stoll, W., Introduction to the value distribution theory of meromorphic functions (Springer-Verlag, New York, 1982).Google Scholar
Utz, W. R., The equation $f'(x)=a f(g(x))$, Bull. Am. Math. Soc. 71 (1965), 138.Google Scholar
van Brunt, B., Marshall, J. C. and Wake, G. C., Holomorphic solutions to pantograph type equations with neutral fixed points, J. Math. Anal. Appl. 295 (2004), 557–569.CrossRefGoogle Scholar
Vitter, A., The lemma of the logarithmic derivative in several complex variables, Duke Math. J. 44 (1977), 89–104.CrossRefGoogle Scholar
Wake, G. C., Cooper, S., Kim, H.-K. and van Brunt, B., Functional differential equations for cell-growth models with dispersion, Comm. Appl. Anal. 4 (2000), 561–573.Google Scholar