Hostname: page-component-f554764f5-rj9fg Total loading time: 0 Render date: 2025-04-08T20:08:59.115Z Has data issue: false hasContentIssue false
  • English
  • Français

On joins with group congruences

Published online by Cambridge University Press:  20 January 2009

P. M. Edwards
P. M. Edwards
Affiliation:
Econometrics Department, Monash University, Clayton, Victoria 3168, Australia
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 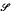be an arbitrary semigroup. A congruence γ on 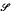is a group congruence if 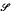/γ is a group. The set of group congruences on 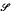is non-empty since 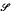× 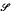is a group congruence. The lattice of congruences on a semigroup 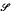will be denoted by 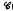(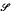) and the set of group congruences on 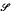will be denoted by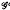 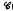(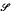). If 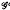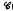(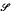) is a lattice then it is modular and γ ∨ ρ = γ ο ρ = ρ ο γ for all γ, ρ ε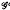 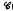(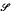). The main result is that γ ν ρ = γ ο ρ ο γ for any γ ε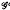 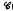(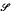) and ρ ε 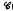(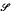) (whence every element of the set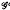 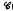(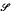) is dually right modular in 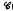(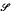). This result has appeared, for particular classes of semigroups, many times in the literature. Also γ ν ρ = γ ο ρ ο γ = ρ ο γ ο ρ for all γ, ρ ε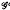 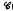(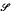) which is similar to the well known result for the join of congruences on a group. Furthermore, if γ ∩ ρ ε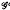 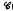(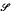) then γ ν ρ = γ ο ρ = ρ ο γ.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 1 , February 1997 , pp. 63 - 67
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1. Clifford, A. H. and Preston, G. B., The algebraic theory of semigroups. Volume I (Mathematical Surveys, 7, American Mathematical Society, Providence, Rhode Island, 1961).CrossRefGoogle Scholar
2. Rao, S. Hanumantha and Lakshmi, P., Group congruences on eventually regular semigroups, J. Austral. Math. Soc. Ser. A 45 (1988), 320–325.CrossRefGoogle Scholar
3. Howie, J. M., The maximum idempotent-separating congruence on an inverse semigroup, Proc. Edinburgh Math. Soc. 14 (1964), 71–79.CrossRefGoogle Scholar
4. Howie, J. M., An introduction to semigroup theory (London Mathematical Society Monographs, 7, Academic Press, London, New York, San Francisco, 1976).Google Scholar
5. Jones, P. R., Joins and meets of congruences on a regular semigroup, Semigroup Forum 30 (1984), 1–16.CrossRefGoogle Scholar
6. La Torre, D. R., Group congruences on regular semigroups, Semigroup Forum 24 (1982), 327–340.CrossRefGoogle Scholar
7. Petrich, Mario, Congruences on inverse semigroups, J. Algebra 55 (1978), 231–256.CrossRefGoogle Scholar
8. Petrich, Mario, Inverse semigroups (John Wiley, New York, 1984).Google Scholar