Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T00:47:52.170Z Has data issue: false hasContentIssue false
  • English
  • Français

On a Boolean algebra of projections constructed by Dieudonné

Published online by Cambridge University Press:  20 January 2009

H. R. Dowson
H. R. Dowson
Affiliation:
University of IllinoisUrbana, Illinois and University of Glasgow
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Dieudonné (4) has constructed an example of a Banach space X and a complete Boolean algebra 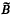of projections on X such that 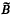has uniform multiplicity two, but for no choice of x1, x2 in X and non-zero E in 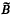is EX the direct sum of the cyclic subspaces clm {Ex1:E∈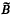} and clm {Ex2:E∈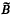}. Tzafriri observed that it could be deduced from Corollary 4 (9, p. 221) that the commutant 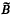′ of 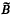is equal to A(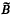), the algebra of operators generated by 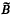in the uniform operator topology. A study of (3) suggested the direct proof of the second property given in this note. From this there follows a simple proof that 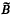has the first property.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 3 , June 1969 , pp. 259 - 262
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1)Bade, W. G.On Boolean algebras of projections and algebras of operators, Trans. Amer. Math. Soc. 80 (1955), 345–359.CrossRefGoogle Scholar
(2)Bade, W. G.A multiplicity theory for Boolean algebras of projections on Banach spaces, Trans. Amer. Math. Soc. 92 (1959), 508–530.CrossRefGoogle Scholar
(3)Dieudonné, J.Sur la bicommutante d'une algèbre d'opérateurs, Portugal. Math. 14 (1955), 35–38.Google Scholar
(4)Dieudonné, J.Champs de vecteurs non localement triviaux, Arch. Math. 7 (1956), 6–10.CrossRefGoogle Scholar
(5)Dowson, H. R.On the commutant of a complete Boolean algebra of projections, Proc. Amer. Math. Soc. 19 (1968), 1448–1452.CrossRefGoogle Scholar
(6)Halperin, I.Function spaces, Canad. J. Math. 5 (1953), 273–288.CrossRefGoogle Scholar
(7)Lorentz, G.Some new functional spaces, Ann. of Math. (2) 51 (1950), 37–55.CrossRefGoogle Scholar
(8)Lorentz, G.On the theory of spaces A, Pacific J. Math. 1 (1951), 411–429.CrossRefGoogle Scholar
(9)Tzafriri, L.On multiplicity theory for Boolean algebras of projections, Israel J. Math. 4 (1966), 217–224.CrossRefGoogle Scholar