No CrossRef data available.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.
Published online by Cambridge University Press: 20 January 2009
Consider a non-holonomic dynamical system specified by the N coordinates qi, and kinetic energy defined by
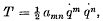
where amn are functions of qi and the dot denotes differentiation with respect to the time t.
page 176 note 1 The summation convention is used, the Roman indices having the range 1 to N.
page 176 note 2 Greek indices have the range 1 to M and have been enclosed in a bracket to indicate that they possess no tensorial property.
page 176 note 3 δαβ = 0 if α ≠ β; δαβ = 1 if α = β.
page 179 note 1 Eisenhart, L. P., Riemannian Geometry (Princeton, 1926), 233.Google Scholar
page 179 note 2 Synge, J. L., Tensorial methods in dynamics, Univ. Toronto Studies App. Maths. Series 2 (1936).Google Scholar
You have
Access