Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T01:03:46.339Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on the Gaussian cardinal-interpolation operator

Published online by Cambridge University Press:  20 January 2009

N. Sivakumar
N. Sivakumar
Affiliation:
Center For Approximation Theory, Department of Mathematics, Texas A&M University, College Station, Tx 77843-3368, U.S.A. E-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

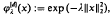Suppose λ is a positive number, and let , x∈Rd, denote the d-dimensional Gaussian. Basic theory of cardinal interpolation asserts the existence of a unique function 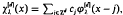, x∈Rd, satisfying the interpolatory conditions 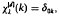, k∈Zd, and decaying exponentially for large argument. In particular, the Gaussian cardinal-interpolation operator 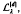, given by 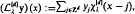, x∈Rd, 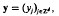, is a well-defīned linear map from ℓ2(Zd) into L2(Rd). It is shown here that its associated operator-norm is 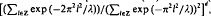, implying, in particular, that 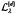is contractive. Some sidelights are also presented.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 40 , Issue 1 , February 1997 , pp. 137 - 149
Copyright
Copyright © Edinburgh Mathematical Society 1997

References

REFERENCES

1. Baxter, B. J. C., Norm estimates for inverses of Toeplitz distance matrices, J. Approx. Theory 79 (1994), 222–242.CrossRefGoogle Scholar
2. Baxter, B. J. C. and Sivakumar, N., On shifted cardinal interpolation by Gaussians and multiquadrics, J. Approx. Theory, to appear.Google Scholar
3. Bellman, R., A brief introduction to Theta functions (Holt, Rinehart and Winston, New York, 1961).Google Scholar
4. Buhmann, M. D., Multivariate cardinal interpolation with radial basis functions, Constr. Approx. 6 (1990), 225–256.CrossRefGoogle Scholar
5. Marsden, M. J. and Mureika, R. A., Cardinal spline interpolation in L 2, Illinois J. Math. 19 (1975), 145–147.CrossRefGoogle Scholar
6. Marsden, M. J., Richards, F. B. and Riemenschneider, S. D., Cardinal spline interpolation operators on lp data, Indiana Univ. Math. J. 24 (1975), 677–689.CrossRefGoogle Scholar
7. Marsden, M. J., Richards, F. B. and Riemenschneider, S. D., Erratum, Indiana Univ. Math. J. 25 (1976), 919.CrossRefGoogle Scholar
8. Richards, F. B., Uniform spline interpolation operators in L2 Illinois J. Math. 18 (1974), 516–521.CrossRefGoogle Scholar
9. Richards, F. B., The Lebesgue constants for cardinal spline interpolation., J. Approx. Theory 14 (1975), 83–92.CrossRefGoogle Scholar
10. Riemenschneider, S. D., Multivariate cardinal interpolation, in Approximation Theory VI: Volume 2 (Chui, C. K., Schumaker, L. L. and Ward, J. D. (eds.), Academic Press, New York, 1989), 561–580.Google Scholar
11. Whittaker, E. T. and Watson, G. N., A course of modern analysis (Cambridge University Press, Cambridge, 1902).Google Scholar
12. Zayed, A. I., Advances in Shannon's sampling theory (CRC Press, Boca Raton, 1993).Google Scholar