All the commonly used rules for the approximate quadrature of areas, such as those of Cotes, Simpson, Tchebychef and Gauss, are based on the assumption that y can be expressed as a rational integral function of x with finite coefficients. A tacit assumption is thus made that 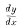is not infinite within the range considered, and it is therefore hardly a matter for surprise that the degree of accuracy obtainable by the use of these rules in the case of a curve which touches the end ordinates is very poor.