Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T00:47:51.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Note on certain related conditions in the theory of Cesaro summability

Published online by Cambridge University Press:  20 January 2009

J. M. Hyslop
J. M. Hyslop
Affiliation:
The University, Glasgow.
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In a recent paper I discussed, for a given series Σan the relation between the conditions

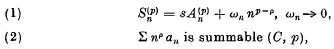
where 0 < ρ < 1 and p is a positive integer. It was there proved (Theorem 14) that (2) implies (1) but that the converse is not necessarily true. My object in this note is to render more precise the connection between (1) and (2) by showing that (2) is equivalent to (1′), where (1′) is (1) with the additional restriction that Σn−1wn is convergent. The proof of this equivalence relation is based on a technique which was introduced and developed by Andersen and is similar to the proofs in my former paper. The note concludes with a brief discussion of the corresponding results for the case ρ = 1.

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 6 , Issue 3 , August 1940 , pp. 165 - 171
Copyright
Copyright © Edinburgh Mathematical Society 1940

References

page 166 note 1 Hyslop, J. M., Proc. Edinburgh Math. Soc. (2), 5 (1938), 182–201. The notation of the present note is the same as the notation of this paper.CrossRefGoogle Scholar

page 166 note 2 Andersen, A. F., Studier over Cesàro's summabilitetsmetode (Copenhagen, 1921).Google Scholar

page 167 note 1 This transformation is contained implicitly in Andersen, , loc. cit., 42.Google Scholar Further details will be found in Hyslop, , loc. cit., 187 (Lemma 5).Google Scholar

page 168 note 1 Hyslop, J. M., loc. cit., 194.Google Scholar

page 168 note 2 For the analogue for absolute summability see Hyslop, J. M., Proc. Edinburgh Math. Soc. (2), 6 (1939), 114–122.CrossRefGoogle Scholar

page 169 note 1 Andersen, A. F., Proc. London Math. Soc. (2), 27 (1928), 39–71, Theorem 2A.CrossRefGoogle Scholar

page 169 note 2 An explicit proof of the equi-summability of these series does'not seem to have been published but, as DrBosanquet, points out, it follows readily enough from a remark of Hardy, and Littlewood, , Proc. London Math. Soc. (2), 27 (1928), 348.Google Scholar

page 169 note 3 Hyslop, J. M., loc. cit., 186, 196 (Theorems 6, 16).Google Scholar