Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oproiu, V.
1977.
Some non-embedding theorems for the Grassmann manifolds G2,n and G3,n.
Proceedings of the Edinburgh Mathematical Society,
Vol. 20,
Issue. 3,
p.
177.
Ilori, Samuel A.
1981.
Nonimmersions of complex Grassmann manifolds.
Proceedings of the Edinburgh Mathematical Society,
Vol. 24,
Issue. 1,
p.
1.
Walgenbach, Markus
2001.
Lower bounds for the immersion dimension of homogeneous spaces.
Topology and its Applications,
Vol. 112,
Issue. 1,
p.
71.


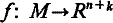 of a differentiable
of a differentiable 