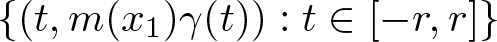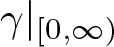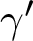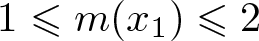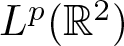1. Introduction
In this study, we analyse a maximal operator defined by a convex function 
$\gamma|_{[0,\infty)}$ and a measurable function 
$m:\mathbb{R}\rightarrow\mathbb{R}$. Specifically, our focus lies on the operator:
\begin{align*}
\mathcal{M}^{m}_{\gamma}f(x_1,x_2):=\sup_{r \gt 0}\frac{1}{2r}\int_{-r}^{r}|f(x_1-t,x_2-m(x_1)\gamma(t))|\text{d}t,
\end{align*} where 
$\gamma:\mathbb{R}\rightarrow\mathbb{R}$ is an extension of 
$\gamma|_{[0,\infty)}$, which is a even or odd function. Recently, Guo, Hickman, Lie and Roos [Reference Guo, Hickman, Lie and Roos13] proved the Lp boundedness of maximal operators 
$\mathcal{M}^{m}_{\gamma}$ for the homogeneous curve 
$\gamma(t) = t^n$, with 
$n \geqslant 2$, assuming that m is measurable. However, the Lp boundedness of 
$\mathcal{M}^{m}_{\gamma}$ for the case n = 1 remains an open problem. So, we focus on flat convex curves, including piecewise linear curves. Given a convex extension 
$\gamma:\mathbb{R}\rightarrow \mathbb{R}$, we define the bounded doubling property for a derivative 
$\gamma'$ as follows:
\begin{align}
\text{there exists a constant}~\omega \gt 1~\text{such that}~\gamma'(\omega |t|)\ge 2\gamma'(|t|)\ \text{for all}~t\in \mathbb{R}.
\end{align}Now, we state the main theorem:
Main Theorem 1.
Let 
$m:\mathbb{R}\rightarrow\mathbb{R}$ be a measurable function such that 
$1\leqslant m(x)\leqslant 2$ for all 
$x\in \mathbb{R}$. Suppose that an extension γ of a convex function 
$\gamma|_{[0,\infty)}$ satisfies the bounded doubling property of 
$\gamma'$ in (1.1), with 
$\gamma(0)=0$. Then, there exists a constant Cω such that 
$\|\mathcal{M}^{m}_{\gamma}\|_{{L^p(\mathbb{R}^2)}\rightarrow L^p(\mathbb{R}^2)}\leqslant C_{\omega,p}$ holds for 
$1 \lt p\leqslant \infty$.
• The theorem can be extended to certain types of piecewise linear curves. Refer to Section 7 in [Reference Carbery, Christ, Vance, Wainger and Watson7] or Remark 5 in [Reference Kim14] for more details. Additionally, the condition (1.1) admits flat convex curves, such as
$\gamma(t)=\text{e}^{-\frac{1}{|t|}}$ and $\text{e}^{-\text{e}^{\frac{1}{|t|}}}$, which are flat at the origin.• By using the dilation technique, we can extend our results to
$\|\mathcal{M}^{m}_{\gamma}\|_{{L^p}\rightarrow L^p}\leqslant C\log_{2}(\frac{b}{a})$ under the assumption $0 \lt a\leqslant m(x)\leqslant b$.
In the view of pointwise convergence, we can drop the assumption 
$1\leqslant m(x_1)\leqslant 2$.
Corollary 1.1. For a measurable function 
$m:\mathbb{R}\rightarrow\mathbb{R}$ and a convex extension γ on 
$\mathbb{R}^1$ passing through the origin with its derivative 
$\gamma'$ satisfying property (1.1), we have
\begin{align*}
\lim_{r\rightarrow0}\frac{1}{2r}\int_{-r}^{r}f(x_1-t,x_2-m(x_1)\gamma(t))\text{d}t=f(x_1,x_2) \text{a.e. }
\end{align*} for 
$f\in L^p(\mathbb{R}^2)$.
The study of maximal operators along flat convex curves has a rich history in Harmonic analysis by itself. In the 1970s, Stein and Wainger [Reference Stein and Wainger24] asked the general class of curves 
$(t,\gamma(t))$ for which there are Lp results for 
$\mathcal{M}^{1}_{\gamma}$. In the 1980s, Carlsson 
$\textit{et al. }$ [Reference Carlsson, Christ, Córdoba, Duoandikoetxea, Rubio de Francia, Vance, Wainger and Weinberg11] proved that 
$\mathcal{M}^{1}_{\gamma}$ is bounded on 
$L^p(\mathbb{R}^2)$ under the bounded doubling condition (1.1). In the 1990s, the study of maximal operators was extended to the curves with a variable coefficient, as demonstrated in [Reference Bennett.4, Reference Carbery, Wainger and Wright9, Reference Carbery, Wainger and Wright10, Reference Kim15, Reference Seeger and Wainger23]. Carbery, Wainger and Wright [Reference Carbery, Wainger and Wright9] established the Lp boundedness of 
$\mathcal{M}^{x_1}_{\gamma}$ along plane curves γ whose derivative satisfies the infinitesimal doubling property. Under the same assumption, Bennett [Reference Bennett.4] extended the L 2 results for 
$\mathcal{M}^{P}_{\gamma}$, where P is a polynomial. As a corollary of our main theorem, we derive the Lp boundedness of 
$\mathcal{M}^{P}_{\gamma}$ under much weaker assumptions on γ.
Corollary 1.2. For a polynomial 
$P:\mathbb{R}\rightarrow\mathbb{R}$ with degree d and a convex extension γ on 
$\mathbb{R}^1$ passing through the origin with its derivative 
$\gamma'$ satisfying property (1.1), there exists a constant 
$C_{\omega, d}$ independent of the coefficients of P such that 
$\|\mathcal{M}^{P}_{\gamma}\|_{{L^p(\mathbb{R}^2)}\rightarrow L^p(\mathbb{R}^2)}\leqslant C_{\omega,d,p}$ for 
$1 \lt p\leqslant \infty$.
Note that the infinitesimal doubling property implies the bounded doubling property. For more details, refer to [Reference Bennett.4].
1.1. Historical background
Zygmund conjecture is a long-standing open problem in harmonic analysis. This question inquires whether the Lipschitz regularity of u is sufficient to guarantee any non-trivial Lp bounds for the maximal operator:
\begin{align*}
\mathcal{M}_{\gamma}^u(f)(x_1,x_2):=\sup_{r \gt 0}\frac{1}{2r}\int_{-r}^{r}|f(x_1-t,x_2-u(x_1,x_2)\gamma(t))|\text{d}t,
\end{align*} where 
$\gamma(t)=t$. Since the discovery of the Besicovitch set in the 1920s, it has been shown that the conjecture is false when the function u is only Hölder continuous C α with α < 1. However, the problem remains open under the Lipschitz assumption for u. In the 1970s, Stein and Wainger [Reference Stein and Wainger24] proposed an analogous conjecture for the Hilbert transform. Regarding the Hilbert transforms along vector fields, Lacey and Li [Reference Lacey and Li18] made a significant progress regarding the regularity of u in 2006, using time–frequency analysis tools. Later, Bateman and Thiele [Reference Bateman and Thiele2] obtained the Lp estimates for the Hilbert transform along a one-variable vector field. Their proof relied on the commutation relation between the Hilbert transform and Littlewood–Paley projection operators, which cannot be directly applied to the maximal operator 
$\mathcal{M}_{\gamma}^m$ due to its sub-linearity. Therefore, the problem for maximal operators remains open. For additional discussion on Stein’s conjecture, we recommend references [Reference Bateman1, Reference Bateman and Thiele2, Reference Lacey and Li17]. In the study of maximal operators, Bourgain [Reference Bourgain5] demonstrated the L 2 boundedness of 
$\mathcal{M}^{u}_{t}$ for real analytic functions u. In 1999, Carbery, Seeger, Wainger and Wright [Reference Carbery, Seeger, Wainger and Wright8] examined the maximal operators 
$\mathcal{M}_{t}^{m}$ along one variable vector field. One of the authors in this paper further extended this result in [Reference Kim16].
Recently, in [Reference Guo, Hickman, Lie and Roos13], Guo et al. investigated the Lp boundedness of 
$\mathcal{M}_{\gamma}^u$ under the Lipschitz assumption for u and homogeneous curve 
$\gamma(t)=t^n$ for n > 1. Later, Liu, Song and Yu [Reference Liu, Song and Yu20] extended the results to more general curves with the condition 
$\left|\frac{t\gamma''(t)}{\gamma'(t)}\right|\sim 1$. A crucial tool used in the proofs of both papers was the local smoothing estimate, which was established in [Reference Beltran, Hickman and Sogge3, Reference Mockenhaupt, Seeger and Sogge21]. For more history, we recommend the study [Reference Lie19] by Victor Lie, which presents a unified approach and includes a more general view of this topic as well as problems related to the concept of non-zero curvature.
1.2. Notation
Let 
$\psi:\mathbb{R}\rightarrow \mathbb{R}$ be a non-negative 
$C^{\infty}$ function supported on 
$[-2,2]$ such that 
$\psi\equiv 1$ on 
$[-1,1]$. Define 
$\varphi(t)=\psi(t)-\psi(2t)$ and 
$\varphi_l(t)=\frac{1}{2^l}\varphi(\frac{t}{2^l})$. Also, define 
$\psi^c(t)=1-\psi(t)$. Note that 
$\sum_{l\in \mathbb{Z}} \varphi\left(\frac{t}{2^l}\right)=1\ \text{for }t\neq0$ and 
$\text{supp}(\varphi)\subset\left\{\frac{1}{2}\leqslant|x|\leqslant2\right\}$. We define the Littlewood–Paley projection 
$\mathcal{L}_sf$ as 
$\widehat{\mathcal{L}_sf}(\xi):=\hat{f}(\xi){\varphi}\left(\frac{\xi_1}{2^s}\right)$. We shall use the notation 
$A\lesssim_d B$ when 
$A\leqslant C_dB$ with a constant 
$C_d \gt 0$ depending on the parameter d. Moreover, we write 
$A\sim_d B$, if 
$A\lesssim_d B$ and 
$B\lesssim_d A$. Let M HL be the Hardy–Littlewood maximal operator and M str be the strong maximal operator. Let χA be a characteristic function, which is equal to 1 on A and otherwise 0. Denote the dyadic pieces of intervals by
\begin{align*}
I_{i}&=[2^{i-1},2^{i+1}]\cup[-2^{i+1},-2^{i-1}],\\
\tilde{I}_{i}&=[2^{i-2},2^{i+2}]\cup[-2^{i+2},-2^{i-2}],
\end{align*} and the corresponding strips by 
$S_i=I_i\times \mathbb{R}$, 
$\tilde{S}_i=\tilde{I}_i\times \mathbb{R}$.
2. Reduction
In this section, we present three propositions that have broad applicability. Let 
$\Gamma:\mathbb{R}^2\rightarrow \mathbb{R}$ be a measurable function and define a general class of operators
\begin{align*}
T_jf(x_1,x_2)&:=\int {f(x_1-t,x_2-\Gamma(x_1,t))}\varphi_j
(t)\text{d}t.
\end{align*}Proposition 2.1. Define 
$T_j^{\text{glo}}f(x_1,x_2):=\psi_{j+4}^c(x_1)T_jf(x_1,x_2)$. Under the measurability assumption of Γ, we have
\begin{align*}
\|\sup_{j}|T_j-T_j^{\text{glo}}|\|_p\leqslant C_p,
\end{align*} for 
$1 \lt p\leqslant \infty$.
Proof. Denote that 
$\tilde{\varphi}(\frac{x}{2^j})=\sum_{k=-3}^{4}\varphi(\frac{x}{2^{j+k}})$, which has a localized support 
$|x|\sim 2^j$. Let 
$T_j^{\text{loc}}$ and 
$T_j^{\text{mid}}$ be operator, defined by
\begin{align*}
T_j^{\text{loc}}f(x_1,x_2)&:=\psi_{j-4}(x_1)T_jf(x_1,x_2),\\
T_j^{\text{mid}}f(x_1,x_2)&:=\tilde{\varphi}{}\bigg(\frac{x_1}{2^j}\bigg)T_{j}f(x_1,x_2).
\end{align*} Then, we can decompose 
$T_j-T_j^{\text{glo}}$ into 
$T_j^{\text{mid}}+T_j^{\text{loc}}$. For the operator 
$T_j^{\text{mid}}$, replace the sup as 
$\ell^p$ sum. Then, we have
\begin{align*}
{\left\|\sup_{j\in \mathbb{Z}}|T_j^{\text{mid}}f|\right\|}_{L^p({\mathbb{R}}^2)}\leqslant{\bigg(\sum_{j\in \mathbb{Z}}{\|T_j^{\text{mid}}f\|}^p_{L^p({\mathbb{R}}^2)}\bigg)}^{\frac{1}{p}}.
\end{align*} Denote 
$F(x_1)=\|f(x_1,\cdot)\|_{L^p(dx_2)}$. By applying Minkowski’s integral inequality and a change of variables, we get the pointwise inequality:
\begin{align}
\begin{split}
\|T_j^{\text{mid}}f(x_1,\cdot)\|_{L^p(dx_2)}&\leqslant\int\bigg(\int|f(x_1-t,x_2-\Gamma(x_1,t))|^pdx_2\bigg)^\frac{1}{p}\varphi_j(t)\text{d}t\\
&\leqslant\int F(x_1-t)\varphi_j(t)dt\lesssim_{\varphi}M_{\text{HL}}F(x_1),
\end{split}
\end{align} where the second inequality follows form the fact that 
$\Gamma(x_1,t)$ is independent of x 2. By (2.1) and the Lp boundedness of M HL, we obtain
\begin{align*}
\bigg(\sum_{j\in \mathbb{Z}}\|T_j^{\text{mid}}f\|^p_{L^p(\mathbb{R}^2)}\bigg)^{\frac{1}{p}}&\leqslant \bigg(\sum_{j}\int\tilde{\varphi}\bigg(\frac{x_1}{2^j}\bigg)|M_{\text{HL}}F(x_1)|^pdx_1\bigg)^{\frac{1}{p}}\lesssim \|f\|_{p}.
\end{align*} which implies the Lp boundedness of 
$f\mapsto \sup_{j}|T_j^{\text{mid}}f|$ for p > 1. For the operator 
$T_j^{\text{loc}}f$, we observe the localization principle:
\begin{align*}
T^{\text{loc}}_jf(x_1,x_2)=T^{\text{loc}}_j(\chi_{S_j}f)(x_1,x_2).
\end{align*} By combining this with 
$\sup_{j\in \mathbb{Z}}\|T_j\|_p \leqslant C$, we get the following estimate:
\begin{align*}
\Big\|\sup_{j\in\mathbb{Z}}|T^{\text{loc}}_jf|\Big\|_p^p&=\sum_{j\in \mathbb{Z}}\int |{T}^{\text{loc}}_{j}\chi_{S_j}f(x_1,x_2)|^p\text{d}x\leqslant C\sum_{j\in \mathbb{Z}}\int |\chi_{S_j}f(x_1,x_2)|^p\text{d}x\lesssim\|f\|_p^p.
\end{align*} Therefore, we prove 
$\|\sup_{j}|T_j-T_j^{\text{glo}}|\|_p\leqslant C_p$ for 
$1 \lt p\leqslant \infty$.
By Proposition 2.1, in order to prove Theorem 1, it suffices to consider the maximal operator defined as
\begin{align*}
f\mapsto \sup_j|T_j^{\text{glo}}f|~,\text{where}~T_j^{\text{glo}}=\psi_{j+4}^cT_j.
\end{align*}Proposition 2.2 (Space Reduction)
Let 
${T}_{j}^{\ell}f(x_1,x_2):=\chi_{S_{\ell}}(x_1,x_2){T}_{j}^{\text{glo}}f(x_1,x_2)$. Then, the following inequality holds:
\begin{align}
\|\sup_{j\in\mathbb{Z}}|{T}^{\text{glo}}_{j}|\|_{L^p\rightarrow L^p}\lesssim \sup_{\ell\in \mathbb{Z}}\|\sup_{j\in\mathbb{Z}}|{T}^{\ell}_{j}|\|_{L^p\rightarrow L^p}.
\end{align}Proof. One can obtain (2.2) from the localization 
$T^{\ell}_jf(x_1,x_2)=T_j^{\ell}(\chi_{\tilde{{S_{\ell}}}}f)(x_1,x_2).$
Combining Proposition 2.1 and Proposition 2.2, we may restrict our attention to the maximal operator defined by 
$
f\mapsto \sup_j|T_j^{\ell}|$, supported on 
$|x_1|\sim 2^{\ell}\gg2^j$.
Proposition 2.3 (Frequency Reduction)
Suppose 
$\Gamma:\mathbb{R}\times [0,\infty)\rightarrow \mathbb{R}$ is measurable on 
$\mathbb{R}^2$ with 
$\Gamma(x_1,0)=0$ satisfying the following conditions:
\begin{align*}
&\text{For every}~x_2\in \mathbb{R},~x_1\mapsto \Gamma(x_1,x_2)~\text{is measurable function.}\\
&\text{For every}~x_1\in \mathbb{R},~x_2\mapsto\Gamma(x_1,x_2)~\text{is convex increasing function.}
\end{align*} Let 
$\widehat{\mathcal{L}_j^{\text{low} }f}(\xi_1,\xi_2):=\hat{f}(\xi_1,\xi_2)\psi(2^j\xi_1)$ for 
$f\in \mathcal{S}(\mathbb{R}^2)$. Then, there exists a constant C independent of Γ such that
\begin{align*}
\sup_{j\in\mathbb{Z}}|T_j(\mathcal{L}_j^{\text{low}}f)(x_1,x_2)|\leqslant C M^{2}M^{1}f(x_1,x_2),
\end{align*}where M i is the Hardy–Littlewood maximal operator taken in the ith variable.
Proof. For 
$g\in \mathcal{S}(\mathbb{R}^1)$ and 
$2^{j-1}\leqslant|t|\leqslant 2^{j+1}$, we have
\begin{align*}
\begin{split}
&\int g(x_1-t-s)\frac{1}{2^j}\check{\psi}\bigg(\frac{s}{2^j}\bigg)ds\lesssim_{\psi} M_{\text{HL}}g(x_1),\\
&\frac{1}{r}\int_{0}^{r} g(x_2-\Gamma(x_1,t))dt\leqslant2M_{\text{HL}}f(x_2-\Gamma(x_1,0))=2M_{\text{HL}}g(x_2),
\end{split}
\end{align*} where the second inequality follows form the convexity of 
$t\mapsto \Gamma(x_1,t)$. For more details, we refer to Lemma 2 in [Reference Cho, Hong, Kim and Woo Yang12] and [Reference Córdoba and Rubio de Francia6]. Since 
$T_j(\mathcal{L}_j^{\text{low}}f)(x_1,x_2)$ is a composition of the above two functions, we obtain the desired pointwise inequality.
Set 
$\widehat{\mathcal{L}_j^{\text{high}}f}(\xi_1,\xi_2)= \hat{f}(\xi_1,\xi_2)\psi^c(2^j\xi_1)$. Following Proposition 2.3, it is enough to show the estimate 
$\|\sup_j|T_j^{\ell}(\mathcal{L}_j^{\text{high}}f)|\|_p\lesssim \|f\|_p$.
3. Proof of main theorem 1
Following the reduction section, we only consider 
$\mathcal{T}_{j}^{\ell}(\mathcal{L}_j^{\text{high}}f)$, which is given by
\begin{align*}
\mathcal{T}_{j}^{\ell}(\mathcal{L}_j^{\text{high}}f)(x_1,x_2):=\psi_{j+4}^c(x_1)\chi_{S_{\ell}}(x)\int {\mathcal{L}_j^{\text{high}}f(x_1-t,x_2-m(x_1)\gamma(t))}\varphi_j(t)\text{d}t,
\end{align*} supported on 
$|x_1|\sim 2^{\ell}\gg 2^j$.
3.1. Main difficulty
In a view of pseudo-differential operator, we write
\begin{align*}
\mathcal{T}_{j}^{\ell}(\mathcal{L}_j^{\text{high}}f)(x_1,x_2)=\int \text{e}^{2\pi i (x_1\xi_1+x_2\xi_2)}b_{j}(x_1,\xi_1,\xi_2)\hat{f}(\xi_1,\xi_2)d\xi_1d\xi_2,
\end{align*} with the symbol 
$b_j(x_1,\xi_1,\xi_2)$ given by
\begin{align*}
b_j(x_1,\xi_1,\xi_2)=\chi_{I_{\ell}}(x_1)\psi^c(2^j\xi_1)\int \text{e}^{-2\pi i (2^jt\xi_1+m(x_1)\gamma(2^jt)\xi_2)}\varphi(t)\text{d}t.
\end{align*} When analysing an oscillatory integral with a phase 
$t\xi_1+m(x_1)\gamma(t)\xi_2$, it is usual to decompose each frequency variable ξ 1 and ξ 2 with dyadic scale. Specifically, in the case of a homogeneous curve, we can even estimate the asymptotic behaviour of oscillatory integral. However, under the flat condition (1.1), this usual approach does not work, as there are no comparablity condition 
$\left|\frac{\gamma'(2t)}{\gamma'(t)}\right|\sim 1$ and a finite type assumption for the curve. To overcome this situation, we will perform an angular decomposition in [Reference Carlsson, Christ, Córdoba, Duoandikoetxea, Rubio de Francia, Vance, Wainger and Weinberg11] for a function f and utilize the method in one of the author’s paper [Reference Kim15].
3.2. Angular decomposition
Set
\begin{align*}
A_j(\xi_1,\xi_2):=\psi\bigg(\frac{\xi_1}{\xi_2 \gamma'(2^{j+1})}\bigg)-\psi\bigg(\frac{\xi_1}{\xi_2 \gamma'(2^{j-1})}\bigg)
\end{align*}and
\begin{align*}
\widehat{\mathcal{A}_jf}(\xi_1,\xi_2)&:=\hat{f}(\xi_1,\xi_2)A_{j}(\xi_1,\xi_2),\\
{\mathcal{A}_j^cf}(x_1,x_2)&:=f(x_1,x_2)-\mathcal{A}_jf(x_1,x_2).
\end{align*}Note that we have the following Littlewood–Paley estimate in [Reference Carlsson, Christ, Córdoba, Duoandikoetxea, Rubio de Francia, Vance, Wainger and Weinberg11]:
\begin{align*}
\bigg\|\bigg(\sum_{j\in \mathbb{Z}}|\mathcal{A}_{j}f|^2\bigg)^\frac{1}{2}\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \|f\|_{L^p(\mathbb{R}^2)}~\text{for}~1 \lt p \lt \infty.
\end{align*} We have 
$\mathcal{A}_{j}\mathcal{L}_{j}^{\text{high}}f(x)=\mathcal{A}_{j}f(x)-
\mathcal{L}_{j}^{\text{low}}\mathcal{A}_{j}f(x)$. Then, it gives
\begin{align*}
|\mathcal{A}_{j}\mathcal{L}_{j}^{\text{high}}f(x_1,x_2)|\lesssim|\mathcal{A}_{j}f(x_1,x_2)|+|M^1\mathcal{A}_{j}f(x_1,x_2)|
\end{align*} from the pointwise estimate 
$|\mathcal{L}_{j}^{\text{low}}f(x_1,x_2)|\lesssim M^1f(x_1,x_2)$. By the vector valued estimate for Hardy–Littlewood maximal operator, the following estimate holds:
\begin{align}
\bigg\|\bigg(\sum_{j\in \mathbb{Z}}|\mathcal{A}_{j}\mathcal{L}_j^{\text{high}}f|^2\bigg)^\frac{1}{2}\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \|f\|_{L^p(\mathbb{R}^2)}\ \text{for}~1 \lt p \lt \infty.
\end{align} We split 
$\mathcal{T}^{\ell}_{j}(\mathcal{L}_j^{\text{high}}f)$ into two terms:
\begin{align*}
\mathcal{T}^{\ell}_{j}(\mathcal{L}_j^{\text{high}}f)=\mathcal{T}^{\ell}_{j}(\mathcal{A}_j\mathcal{L}_j^{\text{high}}f)+\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{j}^{\text{high}}f).
\end{align*}Then, we shall prove the following:
\begin{align}
\bigg\|\sup_{j\in \mathbb{Z}}|\mathcal{T}^{\ell}_{j}(\mathcal{A}_j\mathcal{L}_j^{\text{high}}f)|\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \|f\|_{L^p(\mathbb{R}^2)},
\end{align}
\begin{align}
\bigg\|\sup_{j\in \mathbb{Z}}|\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_j^{\text{high}}f)|\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \|f\|_{L^p(\mathbb{R}^2)}.
\end{align}We can obtain the estimate (3.2) for p = 2 from the following process:
\begin{align}
\bigg\|\bigg(\sum_{j\in \mathbb{Z}}|\mathcal{T}^{\ell}_{j}(\mathcal{A}_j\mathcal{L}_j^{\text{high}}f)|^2\bigg)^\frac{1}{2}\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \bigg\|\bigg(\sum_{j\in \mathbb{Z}}|\mathcal{A}_{j}\mathcal{L}_{j}^{\text{high}}f|^2\bigg)^\frac{1}{2}\bigg\|_{L^p(\mathbb{R}^2)}\lesssim \|f\|_{p}.
\end{align} Furthermore, the range of p can be extended by a bootstrap argument detailed in Section 3.4. In the following proposition, we focus particularly on the term 
$\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{j}^{\text{high}}f)$ and prove the estimate (3.3). Furthermore, the range of p can be extended by a bootstrap argument detailed in Section 3.4. In the following proposition, we focus particularly on the term 
$\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{j}^{\text{high}}f)$ and prove the estimate (3.3).
Proposition 3.1. Define the Littlewood–Paley projection 
$\widehat{\mathcal{L}_jf}(\xi_1,\xi_2):=\hat{f}(\xi_1,\xi_2)$
$\varphi(\frac{\xi_1}{2^j})$ so that 
$\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{j}^{\text{high}}f)=\sum_{n=0}^{\infty}\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{n-j}f)$. For 
$f\in L^p(\mathbb{R}^2)$, It holds that
\begin{align}
&\left\|\sup_{j\in\mathbb{Z}}|\mathcal{T}^{\ell}_{j}(\mathcal{A}_j^c\mathcal{L}_{n-j}^{}f)|\right\|_{L^p(\mathbb{R}^2)} \le C2^{-\varepsilon_p n}\|f\|_{L^p(\mathbb{R}^2)},
\end{align} for 
$1 \lt p \lt \infty$ and 
$n\geqslant0$.
Note that we need the following:
Lemma 3.1 (Reduction to one variable operator)
Consider the two operators 
$\mathcal{R}_1$ and 
$\mathcal{R}^{\lambda}_2$, given by
\begin{align*}
\mathcal{R}_1f(x_1,x_2)&:=\int_{\mathbb{R}^2} e^{2\pi i (x_1\xi_1+x_2\xi_2)}a(x_1,\xi_1,\xi_2)\hat{f}(\xi_1,\xi_2) d\xi_1d\xi_2, \\
{\mathcal{R}}^{\lambda}_2g(x_1)&:=\int_{\mathbb{R}} e^{2\pi i x_1\xi_1}a(x_
1,\xi_1,\lambda)\hat{g}(\xi_1) d\xi_1.
\end{align*} for 
$f\in \mathcal{S}(\mathbb{R}^2)$ and 
$g\in \mathcal{S}(\mathbb{R})$. Then, 
$\|\mathcal{R}_1\|_{L^2(\mathbb{R}^2)\rightarrow L^2(\mathbb{R}^2)}\leqslant\sup_{\lambda\in \mathbb{R}}\|\mathcal{R}^{\lambda}_2\|_{L^2(\mathbb{R})\rightarrow L^2(\mathbb{R})}$.
Proof of Lemma 3.1
Consider a function 
$f\in \mathcal{S}(\mathbb{R}^2)$ with 
$\|f\|_{L^2(\mathbb{R}^2)}=1$. Denote 
$\mathcal{F}_2f(x_1,\xi_2)=g_{\xi_2}(x_1)$. By Plancheral’s theorem with respect to x 2, we get
\begin{align*}
\|\mathcal{R}_1f\|_2^2&=\int \bigg|\int_{\mathbb{R}^2} \text{e}^{2\pi i (x_1\xi_1+x_2\xi_2)}a(x_1,\xi_1,\xi_2)\hat{f}(\xi_1,\xi_2) d\xi_1d\xi_2\bigg|^2\text{d}x_1\text{d}x_2\\
&=\int \bigg|\int_{\mathbb{R}} \text{e}^{2\pi i x_2\lambda}\mathcal{R}^{\lambda}_2g_{\lambda}(x_1)\text{d}\lambda\bigg|^2\text{d}x_2\text{d}x_1\\
&=\int|\mathcal{R}^{\lambda}_2g_{\lambda}(x_1)|^2 \text{d}x_1\text{d}\lambda\leqslant \sup_{\lambda\in \mathbb{R}}\|\mathcal{R}^{\lambda}_2\|_{L^2(\mathbb{R})\rightarrow L^2(\mathbb{R})}^2\int|g_{\lambda}\|^2_{L^2(\mathbb{R})}\text{d}\lambda.
\end{align*}which yields the desired estimate.
3.3. Proof of Proposition 3.1
We shall prove 
$\|\mathcal{T}^{\ell}_j\mathcal{L}_{n-j}\mathcal{A}_j^c\|_{L^2(\mathbb{R}^2)\rightarrow L^2(\mathbb{R}^2)}\lesssim 2^{-\frac{n}{2}}$, which implies
\begin{align*}
\begin{split}
\bigg\|\sup_{j}|\mathcal{T}_j^{\ell}(\mathcal{L}_{n-j}\mathcal{A}_j^cf)|\bigg\|_{2}^2
&\lesssim \sum_{j}\|\mathcal{T}_{j}^{\ell}\mathcal{L}_{n-j}\mathcal{A}_j^c(\mathcal{L}_{n-j}f)\|_{2}^2\\
&\lesssim {2^{-n}}\|\sum_{j}\mathcal{L}_{n-j}f\|_{2}^2={2^{-n}}\|f\|_{2}^2 .
\end{split}
\end{align*} We write 
$\mathcal{T}^{\ell}_j\mathcal{L}_{n-j}\mathcal{A}_j^cf$ as
\begin{align*}
\mathcal{T}^{\ell}_j\mathcal{L}_{n-j}\mathcal{A}_j^cf(x_1,x_2)=\int \text{e}^{2\pi i (x_1\xi_1+x_2\xi_2)}a_j(x_1,\xi_1,\xi_2)\hat{f}(\xi_1,\xi_2)\text{d}\xi_1 \text{d}\xi_2,
\end{align*} with symbol 
$a_j(x_1,\xi_1,\xi_2)$ given by
\begin{align*}
\chi_{I_{\ell}}(x_1)\varphi\bigg(\frac{\xi_1}{2^{n-j}}\bigg)A_j^c(\xi_1,\xi_2)\int_{\mathbb{R}} \text{e}^{-2\pi i (2^jt\xi_1+m(x_1)\gamma(2^jt)\xi_2)}\varphi(t)\text{d}t.
\end{align*}By Lemma 3.1, to prove (3.5), it suffices to show
\begin{equation*}\|\mathcal{R}^{\lambda}_j\|_{L^2(\mathbb{R})\rightarrow L^2(\mathbb{R})}\leqslant c_12^{-c_2n},\end{equation*} where c 1 and c 2 are constants independent of j and λ and 
$\mathcal{R}^{\lambda}_jg(x):=\int \text{e}^{2\pi i x\xi}a_j(x,\xi,\lambda)\hat{g}(\xi)\text{d}\xi$ for 
$g\in \mathcal{S}(\mathbb{R})$. Note that 
$x\in \mathbb{R}$ and 
$\xi\in \mathbb{R}$. Hereafter, we omit j and λ in operators for simplicity. Observe that we write 
$\mathcal{R}$ with kernel K
\begin{align*}
\mathcal{R}g(x)&=\int \text{e}^{2\pi i x\xi}a_j(x,\xi,\lambda)\bigg(\int \text{e}^{-2\pi i y\xi }g(y)\text{d}y\bigg)\text{d}\xi\\
&=\int K(x,y)g(y) \text{d}y,
\end{align*}where
\begin{align*}
K(x,y):=\chi_{I_{\ell}}(x)\int \text{e}^{-2\pi i \lambda m(x)\gamma(2^jt)}\bigg(\int \text{e}^{2\pi i (x-2^jt-y)\xi}\varphi\bigg(\frac{\xi_1}{2^{n-j}}\bigg)\widehat{A_j^c}(\xi,\lambda)d\xi\bigg)\varphi(t)\text{d}t.
\end{align*} Recall that 
$|x|\sim 2^{\ell}\gg 2^j$ and denote
\begin{align*}
Q_k&:=\{x\in \mathbb{R} : 2^{\ell-1}+k\cdot2^j\leqslant|x| \lt 2^{\ell-1}+(k+1)\cdot 2^j \},\\
Q'_k&:=\{x\in \mathbb{R} : 2^{\ell-1}+(k-4)\cdot2^j\leqslant|x| \lt 2^{\ell-1}+(k+5)\cdot 2^j \} ,
\end{align*}for each integer k. We define the functions
\begin{align*}
G_k(x,y)&:=K(x,y)\chi_{Q_k}(x)\chi^c_{{Q}'_k}(y),\\
B_k(x,y)&:=K(x,y)\chi_{Q_k}(x)\chi_{{Q}'_k}(y)
\end{align*} and use them to split the operator 
$\mathcal{R}$ as
\begin{align*}
\mathcal{R}g(x)=&\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\bigg(\int G_k(x,y)g(y)\text{d}y+\int B_k(x,y)g(y)\text{d}y\bigg)\\
:=& \sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\bigg(\mathcal{G}_kg(x)+\mathcal{B}_kg(x)\bigg).
\end{align*}Then, we shall prove the following:
Lemma 3.2. There exist constants C 1 and C 2 independent of 
$j, \ell$ and λ such that
\begin{align}
&\bigg\|\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\mathcal{G}_k\bigg\|_{L^2(\mathbb{R})\rightarrow L^2(\mathbb{R})}\leqslant C_1 2^{-n},
\end{align}
\begin{align}
&\bigg\|\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\mathcal{B}_k\bigg\|_{L^2(\mathbb{R})\rightarrow L^2(\mathbb{R})}\leqslant C_2 2^{-\frac{n}{2}}.
\end{align}Proof of (3.6)
Recall that
\begin{align*}
K_{}(x,y):=\int \text{e}^{-2\pi i \lambda m(x)\gamma(2^jt)}\bigg(\int \text{e}^{2\pi i (x-2^jt-y)\xi}\varphi\bigg(\frac{\xi}{2^{n-j}}\bigg)A_j^c(\xi,\lambda)\text{d}\xi\bigg)\varphi(t)\text{d}t.
\end{align*}We build our proof upon the following observation:
\begin{align}
&|G_{k}(x,y)|\lesssim \frac{2^j}{2^n|x-y|^2}\chi_{Q_k}(x)\psi^c\bigg(\frac{|x-y|}{2^j}\bigg) .
\end{align}Proof of (3.8)
Note that 
$supp(\psi^c)\subset \left\{|x| \gt \frac{1}{2}\right\}$. We utilize the integration by parts twice with respect to ξ. Then, we get
\begin{align*}
\bigg|\int \text{e}^{2\pi i (x-2^jt-y)\xi}\varphi_{n-j}(\xi)A_j^c(\xi,\lambda)\text{d}\xi\bigg|&\lesssim \frac{1}{(x-2^jt-y)^2}\int\bigg|\partial_{\xi}^2\bigg[\varphi\bigg(\frac{\xi}{2^{n-j}}\bigg)A_j^c(\xi,\lambda)\bigg]\bigg|\text{d}\xi\\
&\lesssim \frac{2^j}{2^n}\cdot \frac{1}{(x-2^jt-y)^2}.
\end{align*} Since 
$|x-2^jt-y| \gt rsim |x-y|$ on 
$x\in Q_k$, 
$y\in \mathbb{R}\setminus Q_k'$ for 
$\frac{1}{2}\leqslant t\leqslant 2$, we get the desired estimate.
We shall deduce the following estimate:
\begin{align}
\begin{split}
\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\bigg(\int{|G_k(x,y)|}\text{d}x+\int{|G_{k}(x,y)|}\text{d}y\bigg)\lesssim {2^{-n}}.
\end{split}
\end{align}Proof of (3.9)
By estimate (3.8) and the disjointness of Qks, we have
\begin{align*}
\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\int{|G_k(x,y)|}\text{d}x&\lesssim \frac{2^j}{2^n}\sum_{k}\int_{|x-y| \gt 2^j}\frac{\chi_{Q_k}(x)}{|x-y|^2}\text{d}x\\
&\lesssim \frac{2^j}{2^n}\cdot \int_{|x| \gt 2^j}\frac{1}{|x|^2}\text{d}x={2^{-n}}.
\end{align*}and the second estimate also holds by the similar way.
By Schur’s lemma with the estimate (3.9), we finish the proof of (3.6).
Proof of (3.7)
For the operator 
$\mathcal{B}_k$, denote 
$g_k(y)=\chi_{Q_k'}(y)g(y)$. By the localization principle, we have
\begin{align}
\bigg\|\sum_{k=0}^{3\cdot2^{\ell-j-1}-1}\mathcal{B}_k\bigg\|_{L^2\rightarrow L^2}\lesssim \sup_{k\in \mathbb{Z}}\bigg(\sup_{\|g_k\|_2=1}{\|\mathcal{B}_kg_k\|_2}\bigg).
\end{align} To estimate 
$\|\mathcal{B}_kg_k\|_2$, we write it with the symbol expression again, which is
\begin{align*}
\mathcal{B}_kg_k(x)=\int \text{e}^{2\pi i x\xi}\chi_{Q_k}(x)a_j(x,\xi,\lambda)\widehat{g_k}(\xi)\text{d}\xi,
\end{align*}where
\begin{align*}
a_j(x,\xi,\lambda)=\chi_{I_{\ell}}(x)\varphi\bigg(\frac{\xi}{2^{n-j}}\bigg)A_j^c(\xi,\lambda)\int \text{e}^{-2\pi i (2^jt\xi+m(x_1)\gamma(2^jt)\lambda)}\varphi(t)\text{d}t,
\end{align*}Observe that
\begin{align}
|a_j(x,\xi,\lambda)|\lesssim \frac{1}{2^j|\xi|}.
\end{align}Proof of (3.11)
From the support of 
$A^c_j(\xi,\lambda)$, we have 
$|\frac{\xi}{\lambda}|\nsim|\gamma'(2^jt)|$ for 
$|t|\sim1$. This enables us to apply the integration by parts with respect to variable t. Then, we get
\begin{align*}
&\bigg|\int \text{e}^{-2\pi i (\xi 2^jt+\lambda m(x)\gamma(2^jt))}\varphi(t)\text{d}t\bigg|\\
&\quad \lesssim \bigg|\int \text{e}^{-2\pi i (\xi 2^jt+\lambda m(x)\gamma(2^jt))}\partial_t\bigg(\frac{\varphi(t)}{2^j(\xi+\lambda m(x)\gamma'(2^jt))}\bigg)\text{d}t\bigg|\\
&\quad \lesssim \int \frac{|2^j\lambda m(x)2^j\gamma''(2^jt)|}{\{2^j(\xi+\lambda m(x)\gamma'(2^jt))\}^2}\cdot{\varphi(t)}\text{d}t+\int \frac{|\varphi'(t)|}{|2^j(\xi+\lambda m(x)\gamma'(2^jt))|}\text{d}t\\
&\quad \lesssim \int \frac{|\varphi'(t)|}{|2^j(\xi+\lambda m(x)\gamma'(2^jt))|}dt\lesssim \frac{1}{2^{j}|\xi|}.
\end{align*}Then, we get the desired estimate.
From the observation (3.11), it is easy to check
\begin{align*}
\int|\chi_{Q_k}(x)a_j(x,\xi,\lambda)|\text{d}x\lesssim {2^{-(n-j)}},&\\
\int|a_j(x,\xi,\lambda)|\text{d}\xi\lesssim {2^{-j}}.&
\end{align*}By Schur’s lemma with the above estimate and (3.10), we obtain (3.7) in Lemma 3.2.
3.4. A bootstrap argument for the proof of Theorem 1
In the spirit of Nagel, Stein and Wainger [Reference Nagel, Stein and Wainger22], we claim that
Lemma 3.3. If 
$\|\sup_{j}|\mathcal{T}_j^{\ell} f|\|_{L^p(\mathbb{R}^2)}\leqslant C_1\|f\|_{L^p(\mathbb{R}^2)}$ and 
$\|\mathcal{T}_j^{\ell} f\|_{L^r(\mathbb{R}^2)}\leqslant C_2\|f\|_{L^r(\mathbb{R}^2)}$ for 
$1 \lt r \lt \infty$,
\begin{align}
&\bigg\|\left(\sum_j|\mathcal{T}_j^{\ell}f_{j}|^{2} \right)^{\frac{1}{2}}\bigg\|_{L^{q}(\mathbb{R}^2)}\leqslant (C_1C_2)^{\varepsilon_q}\bigg\|\left(\sum_j|{f_{j}}|^{2}\right)^{\frac{1}{2}}\bigg\|_{L^{q}(\mathbb{R}^2)}
\end{align} holds for all q with 
$\frac{1}{q} \lt \frac{1}{2}(1+\frac{1}{p})$.
Proof. Consider vector valued functions 
$\mathfrak{f}=\{f_j\}$ and 
$\mathfrak{Tf}=\{\mathcal{T}_j^{\ell}f_j\}$. Since the operator 
$\mathcal{A}_j$ is a positive, it follows that 
$\|\mathfrak{Tf}\|_{L^p({\mathbb{R}}^2,l^\infty)}\lesssim\|\mathfrak{f}\|_{L^p({\mathbb{R}}^2,l^\infty)}$ and 
$\|\mathfrak{Tf}\|_{L^r({\mathbb{R}}^2,l^r)}$ 
$\lesssim \|\mathfrak{f}\|_{L^r({\mathbb{R}}^2,l^r)}$ for r near 1. Applying the Riesz–Thorin interpolation for vector-valued function, we get the conclusion.
Combining (3.4), Proposition 2.3 and Proposition 3.1, we obtain the estimate
\begin{align}
\bigg\|\sup_{j\in \mathbb{Z}} |\mathcal{T}_{j}^{\ell}f|\bigg\|_{p}\leqslant C_p\|f\|_{p}
\end{align}for p = 2. Moreover, we have
\begin{align}
\|\mathcal{T}_{j}^{\ell}f\|_{r}\leqslant\|f\|_{r}
\end{align} for r > 1. By using Lemma 3.3 with (3.13) and (3.14), we obtain (3.12) for 
$\frac{4}{3} \lt p\leqslant 2$. Then, by setting 
$\{f_j\}_{j\in \mathbb{Z}}=\{\mathcal{A}_j^c\mathcal{L}_{n-j}f\}_{j\in \mathbb{Z}}$ in (3.12) and applying interpolation with the decay estimate (3.5), we obtain Proposition 3.1 for 
$\frac{4}{3} \lt p\leqslant 2$. To treat the bad part in (3.4), set 
$\{f_j\}_{j\in \mathbb{Z}}=\{\mathcal{A}_j\mathcal{L}_j^{\text{high}}f\}_{j\in \mathbb{Z}}$. Then, we apply Lemma 3.3 again to get the first inequality of (3.4), which implies (3.13) for 
$\frac{4}{3} \lt p\leqslant 2$. We can iteratively apply Lemma 3.3 with a wider range of p until we get (3.13) for all p > 1. With this, we complete the proof of Main Theorem 1.
4. Application
In this section, we shall prove Corollary 1.1 and Corollary 1.2.
4.1. Proof of Corollary 1.1
For a measurable function 
$m:\mathbb{R}\rightarrow\mathbb{R}$, denote that
\begin{align*}
&S_r^mf(x_1,x_2)=\frac{1}{2r}\int_{-r}^{r}f(x_1-t,x_2-m(x_1)\gamma(t))\text{d}t,\\
&\tilde{E}^k=\{(x_1,x_2)\in\mathbb{R}^2: 2^{k}\leqslant m(x_1)\leqslant 2^{k+1}\}.
\end{align*}By Main Theorem 1 and the second part of Remark 1.1, one can easily check that
\begin{align}
\|\sup_{r \gt 0}|\chi_{\tilde{E}^k}(\cdot)S_r^mf|\|_p\lesssim \|f\|_p.
\end{align} To prove Corollary 1.1, it suffices to show that for each α > 0 and 
$k\in \mathbb{Z}$, the set
\begin{align*}
E_\alpha^k=\bigg\{(x_1,x_2)\in \tilde{E}^k:\limsup_{r\rightarrow0}|S_r^mf(x_1,x_2)-f(x_1,x_2)| \gt 2\alpha\bigg\}
\end{align*} has measure zero. Consider a continuous function gɛ of compact support with 
$\|f-g_{\varepsilon}\|_p \lt ~\varepsilon$. One can see that 
$\limsup_{r\rightarrow0}|S_r^mf(x_1,x_2)-f(x_1,x_2)|\leqslant \mathcal{M}_{\gamma}^{m}(f-g_{\varepsilon})(x)+|g_{\varepsilon}(x)-f(x)|.$ For 
$F_{\alpha}^k$ and 
$G_{\alpha}^k$, defined by
\begin{align*}
&F_{\alpha}^k=\{x\in E_{\alpha}^k:\mathcal{M}_{\gamma}^{m}(f-g_{\varepsilon})(x) \gt \alpha\},\\
&G_{\alpha}^k=\{x\in E_{\alpha}^k:|f(x)-g_{\varepsilon}(x)| \gt \alpha\},
\end{align*} we have 
$m(E_{\alpha}^k)\leqslant m(F_{\alpha}^k)+m(G_{\alpha}^k)$. Applying estimate (4.1), we get
\begin{align*}
m(F_{\alpha}^k)+m(G_{\alpha}^k)\leqslant \frac{2\varepsilon^p}{\alpha^p}.
\end{align*} As 
$\varepsilon\rightarrow 0$, we get the conclusion.
4.2. Proof of Corollary 1.2
In order to achieve our goal of removing the dependence of the coefficients of polynomial P on factors other than its degree, we consider the following lemma.
Lemma 4.1. Given a polynomial P with degree d, we can find a partition 
$\{s_0,s_1,s_2,\dots,s_{n(d)}\}$ such that for each interval 
$[s_i,s_{i+1}]$, there exists a pair 
$(m_i,s_{j_i})$ with 
$1\leqslant m_i\leqslant d$, satisfying
\begin{align}
{\sup_{x\in[s_i,s_{i+1}]}{\frac{|P(x)|}{|x-s_{j_i}|^{m_{i}}}}}\sim_d{\inf_{x\in[s_i,s_{i+1}]} \frac{|P(x)|}{|x-s_{j_i}|^{m_{i}}}}.
\end{align}Proof of Lemma 4.1
We seek to construct a partition 
$\mathcal{P} = \{s_1, s_2, ..., s_{n(d)}\}$ of 
$(-\infty,\infty)$ such that, for each subinterval 
$[s_i, s_{i+1}]$, there exist non-negative integers mi and ji satisfying (4.2). Consider a polynomial P(x) represented by the following expression:
\begin{align*}
P(x) = \prod_{i=1}^{d_1} (x - \alpha_i)^{q_i},
\end{align*} where αi are distinct real numbers. Let 
$U_i=\{x\in\mathbb{R}: |x-\alpha_i| \lt |x-\alpha_k| \text{ for all } k=1,\dots,d_1\}$. For each i and k, let 
$\mathcal{U}_i^{k}(1)=\{x\in U_i:2|x-\alpha_i|\geqslant |x-\alpha_k| \}$ and 
$\mathcal{U}_i^{k}(0)=\{x\in U_i:2|x-\alpha_i| \lt |x-\alpha_k| \}$. Then, for any 
$x\in \mathbb{R}$, there exists an index i such that 
$x\in U_i$. We define the set-valued function Fi on 
$\{0,1\}^{d_1}$ by 
$F_i(a)=\bigcap_{k=1}^{d_1}\mathcal{U}_{i}^k(a_k)$ for 
$a=(a_k)\in\{0,1\}^{d_1}$. By using the set-valued function F, we can decompose each set Ui into a finite number of disjoint open intervals, that is,
\begin{align*}
U_i&=\mathcal{U}_{i}^k(0)\cup\mathcal{U}_{i}^k(1)=\bigcap_{k=1}^{d_1}\bigg(\mathcal{U}_{i}^k(0)\cup\mathcal{U}_{i}^k(1)\bigg)= \bigcup_{a\in\{0,1\}^{d_1}} F_i(a).
\end{align*} For each interval 
$F_i(a)=[s_i,s_{i+1}]$, we take 
$m=\sum_{\{k:a_k=1\}}q_k$ and 
$s_{j_i}=\alpha_i$. Observe that we have the following inequalities for each fixed i:
\begin{align*}
& {|x-\alpha_k|}\sim{|x-\alpha_i|^{}}~\text{for all}~k~\text{such that}~a_k=1, \\
&{|x-\alpha_k|^{}}\sim{|\alpha_i-\alpha_k|^{}}~\text{for all}~k~\textrm{such that}~a_k=0.
\end{align*} By using these observation, we have (4.2) on 
$[s_i,s_{i+1}]$.
To handle a general polynomial, we can employ a similar approach. First, we can express the polynomial as
\begin{align*}
P(x) = \prod_{i=1}^{d_1} (x - \alpha_i)^{q_i}\prod_{i=1}^{d_2}\{(x-\beta_i)^2+\delta_i^2\}^{r_i}.
\end{align*} To treat this, we give one more criterion comparing between 
$2|x-\alpha_i|$ and 
$\max\{|x-\beta_k|,|\delta_k|\}$ instead of 
$|x-\alpha_k|$. Then. the last part can be proved similarly.
Proof of the Corollory 1.2
Given a polynomial P(x), we obtain a partition 
$\mathcal{P}=\{s_0,s_1,\dots,s_{n(d)}\}$ from Lemma 4.1. We then decompose 
$\mathcal{M}_{\gamma}^{P}f(x)$ as
\begin{align*}
\mathcal{M}_{\gamma}^{P}f(x) = \sum_{i=0}^{n(d)}\chi_{[s_i,s_{i+1}]}(x)\mathcal{M}_{i}f(x),
\end{align*} where 
$\mathcal{M}_{i}f(x):=\chi_{[s_i,s_{i+1}]}(x)\mathcal{M}_{\gamma}^{P}f(x)$. To complete the proof, it suffices to demonstrate that
\begin{align*}
\|\mathcal{M}_{i}f\|_p\leqslant C_{d}\|f\|_{p}.
\end{align*} By Lemma 4.1, there exists a pair 
$(m_i,s)$ such that the following holds for 
$[s_{i},s_{i+1}]$:
\begin{align*}
{\sup_{x_1\in[s_i,s_{i+1}]}{\frac{|P(x_1)|}{|x_1-s|^{m_{i}}}}}\sim_d{\inf_{x_1\in[s_i,s_{i+1}]} \frac{|P(x_1)|}{|x_1-s|^{m_{i}}}}.
\end{align*} Denote that 
$g_s(x_1,x_2):=f(x_1+s ,x_2)$ and consider the estimate
\begin{align*}
\|\mathcal{M}_{i}f\|_p^p=\int_{s_i-s}^{s_{i+1}-s}\int_{\mathbb{R}} \bigg(\sup_{r \gt 0}\frac{1}{r}\int_0^{r}{|g_s(x_1-t,x_2-P(x_1+s)\gamma(t))|}dt\bigg)^p\text{d}x_2\text{d}x_1.
\end{align*} By applying Proposition 2.2, we can reduce matters to 
$|x_1|\sim 2^{\ell}$:
\begin{align}
\bigg\|\sup_{j\in \mathbb{Z}}|\mathcal{P}_j^{\ell}g_s|\bigg\|_{p}\leqslant C_d \|f\|_{p},
\end{align} where 
$\mathcal{P}_{j}^{\ell}g_s(x)$ is defined as
\begin{align*}
\mathcal{P}_{j}^{\ell}g_s(x):=\chi_{I_{\ell}}(x_1)\psi_{j+4}^c(x_1)\int {g_s(x_1-t,x_2-P(x_1+s)\gamma(t))}\varphi_j(t)\text{d}t,
\end{align*} for 
$\ell$ such that 
$[2^{\ell-1},2^{\ell+1}]\cap [s_i-s,s_{i+1}-s]\neq \emptyset$. To prove (4.3), it is enough to check the hypothesis of Remark 1.1:
\begin{align*}
\frac{\sup_{x}{|P(x+s)|}}{\inf_{x}|P(x+s)|}\lesssim_d \frac{2^{(\ell+1)m_i}}{2^{(\ell-1)m_i}}\lesssim_d 1~\text{for}~|x|\in [2^{\ell-1},2^{\ell+1}],
\end{align*} where 
$1\leqslant m_i\leqslant d$. This implies the conclusion.
Acknowledgements
J. Kim was supported by the Ministry of Education of the Republic of Korea and the National Research Foundation of Korea under grant NRF-2015R1A2A2A01004568. J. Oh was supported by the National Research Foundation of Korea under grant NRF-2020R1F1A1A01048520 and is currently supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education (RS-2024-00461749).
