Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T00:26:58.895Z Has data issue: false hasContentIssue false
  • English
  • Français

A local mean value theorem for the complex plane

Published online by Cambridge University Press:  20 January 2009

J. M. Robertson
J. M. Robertson
Affiliation:
Washington State University, Pullman, Washington—99163
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The equation

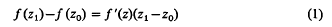
need not have a solution z in the complex plane, even when ƒ is entire. For example, let ƒ(z) = ez, z1 = z0+2kπi. Thus the classical mean value theorem does not extend to the complex plane. McLeod has shown (2) that if ƒ is analytic on the segment joining z1 and z0, then there are points w1 and w2 on the segment such that 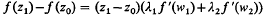where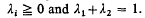

The purpose of this article is to give a local mean value theorem in the complex plane. We show that there is at least one point z satisfying (1), which we will call a mean value point, near z1 and z0 but not necessarily on the segment joining them, provided z1 and z0 are sufficiently close. The proof uses Rouché's Theorem (1).

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 16 , Issue 4 , December 1969 , pp. 329 - 331
Copyright
Copyright © Edinburgh Mathematical Society 1969

References

REFERENCES

(1) Hille, E.Analytic Function Theory, Vol. 1 (Ginn and Co., 1959).Google Scholar
(2) Mcleod, R. M., Mean value theorems for vector valued functions, Proc. Edinburgh Math. Soc. (2) 14 (1965), 197–209.CrossRefGoogle Scholar