Article contents
Gauss' Theorem in a General Space-time
Published online by Cambridge University Press: 20 January 2009
Extract
In classical mechanics Gauss' Theorem for a gravitational field states that, if S is a closed surface and N the component of gravitational force along the outward normal, then

where β is the Newtonian constant of gravitation and M is the total mass inside S. This result has recently been extended to general relativity by E. T. Whittaker,1 who, however, considered only the case of a statical gravitational field, the line-element of which is given by2
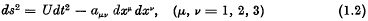
where the coefficients U and αμν are independent of t. It is not immediately clear from his work whether the results are extensible to more general space-times.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 4 , Issue 3 , August 1935 , pp. 144 - 158
- Copyright
- Copyright © Edinburgh Mathematical Society 1935
References
page 144 note 1 Proe. Boy. Soc. (A) 149 (1935), 384.CrossRefGoogle Scholar
page 144 note 2 The summation convention for repeated suffixes is employed throughout this paper, and the velocity of light in vacuo is taken as unity. Greek suffixes will take the values 1 to 3 only. Latin suffixes, used below, take the values 0 to 3.
page 145 note 1 I am indebted to a referee whose criticism of the physical aspect of this paperled to the re-writing of the latter half of § 1.
page 146 note 1 Whittaker, , loc. cit., equation (2.2). CfWalker, , page 173 of the present volume of these Proceedings.Google Scholar
page 147 note 1 A mental picture may be formed by imagining the number of dimensions of spacetime reduced to three. The spatial hypersurfaces f = const. are then represented by a family of surfaces f = const., the observers' world-lines by the orthogonal trajectories of the family, and the surface S at every instant by a closed curve in one of the surfaces f. The orthogonal trajectories passing through this curve generate a surface which is the three-dimensional analogue of the tubular hypersurface.
page 148 note 1 The negative sign is taken because the vectors ni and gi are both space-like, and the fundamental quadratic form should thus be taken negatively (![]() ). That this is so is most easily seen by considering the angle θ(=0) which a unit spacelike vector such as ni makes with itself. Since n in i = – 1, we have cos θ= – n in i.
). That this is so is most easily seen by considering the angle θ(=0) which a unit spacelike vector such as ni makes with itself. Since n in i = – 1, we have cos θ= – n in i.
page 148 note 2 Synge, , Trans. Roy. Soc. Canada, 28 (1934), 169; see also p. 134. Synge takes the metric with signature (–+ + +) instead of (+ – – –), so that with him time-like and space-like directions have respectively indicators – 1 and + 1. He is apparently the first to have noticed the need for inserting the indicator e in one of the integrals of Green's Theorem.Google Scholar
page 150 note 1 Unless, indeed, Δ1f=1. But in this case the world-lines of the fundamental observers are geodesies, and consequently gi=0, so that (4.10) reduces to the trivial identity 0=0.
page 151 note 1 Veblen, , Invariants of Quadratic Differential Forms (Cambridge Tract No. 24), page 41 (16.1).Google Scholar
page 151 note 2 Eisenhart, , Riemannian Geometry (1926), 113.Google Scholar
page 153 note 1 McConnell, Applications of the Absolute Differential Calculus (1931), 197. The negative sign is taken on the left-hand side of (5.17) because ![]() .Google Scholar
.Google Scholar
page 153 note 2 Loc. cit., page 388, equation (I). CfWalker, , page 173.Google Scholar
page 154 note 1 I am here quoting from Whittaker. CfWeyl, , Space-Time-Matter (1922), p. 214 (71), or EddingtonGoogle Scholar, Mathematical Theory of Relativity (1924), p. 126.Google Scholar
page 154 note 2 It is not legitimate to put v actually equal to zero. For if it were the world-lines of the fundamental observers would coincide with those of the material particles and would therefore be geodesies, so that (cf. second footnote of §4) equation (4.10) would reduce to the trivial identity 0=0 and (5.7) would not in general follow.
page 156 note 1 Eisenhart, Riemannian Geometry, p. 43 (14.13).Google Scholar
page 157 note 1 Eisenhart, op. dt., p. 179, §52.Google Scholar
page 158 note 1 McConnell, op. cit., p. 202 (29);Google Scholar or Eisenhart, op. cit., p. 219Google Scholar, examples 9 and 10; or Levi-Civita, , Absolute Differential Calculus (1927), pp. 259, 260.Google Scholar
page 158 note 1 Eisenhart, , op. cit., p. 168.Google Scholar
- 4
- Cited by


