Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T17:00:44.288Z Has data issue: false hasContentIssue false
  • English
  • Français

Explicit calculations in an infinitesimal singular block of SLn

Part of: Linear algebraic groups and related topics Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  10 February 2022

William Hardesty
William Hardesty*
Affiliation:
School of Mathematics and Statistics F07, University of Sydney, Sydney, NSW2006, Australia ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $G= SL_{n+1}$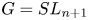 be defined over an algebraically closed field of characteristic $p > 2$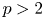. For each $n \geq 1$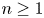, there exists a singular block in the category of $G_1$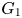-modules, which contains precisely $n+1$ 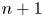irreducible modules. We are interested in the ‘lift’ of this block to the category of $G_1T$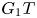-modules. Imposing only mild assumptions on $p$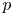, we will perform a number of calculations in this setting, including a complete determination of the Loewy series for the baby Verma modules and all possible extensions between the irreducible modules. In the case where $p$ 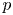is extremely large, we will also explicitly compute the Loewy series for the indecomposable projective modules.

Keywords

representation theoryrestricted Lie algebrasgroup schemesLoewy series

MSC classification

Primary: 20G05: Representation theory
Secondary: 17B45: Lie algebras of linear algebraic groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 19 - 52
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abe, N. and Kaneda, M., The Loewy structure of $G_1T$-Verma modules with singular highest weights, J. Inst. Math. Jussieu 16(4) (2017), 887–898.CrossRefGoogle Scholar
Andersen, H. H., Extensions of modules for algebraic groups, Amer. J. Math. 106(2) (1984), 489–504.CrossRefGoogle Scholar
Andersen, H. H. and Kaneda, M., Loewy series of modules for the first Frobenius kernel in a reductive algebraic group, Proc. London Math. Soc. (3) 59(1) (1989), 74–98.CrossRefGoogle Scholar
Andersen, H. H., Jantzen, J. C. and Soergel, W., Representations of quantum groups at a $p^{t}h$ root of unity and of semisimple groups in characteristic $p$: independence of $p$, Astérisque No. 220 (1994), 321.Google Scholar
Fiebig, P., An upper bound on the exceptional characteristics for Lusztig's character formula, J. Reine. Angew. Math. 673 (2012), 1–31.CrossRefGoogle Scholar
Jantzen, J. C., Darstellungen halbeinfacher algebraischer Gruppen und zugeordnete kontravariante Formen, Bonn. Math. Schr. No. 67 (1973), 53–65.Google Scholar
Jantzen, J. C., Representations of algebraic groups, 2nd edn, Mathematical Surveys and Monographs, Volume 107 (American Mathematical Society, 2003).Google Scholar
Nandakumar, V. and Zhao, G., Categorification via blocks of modular representations for sl(n), preprint (2017). arXiv:1612.06941.Google Scholar
Riche, S., Koszul duality and modular representations of semisimple Lie algebras, Duke Math. J. 154 (2010), 31–134.CrossRefGoogle Scholar
Towers, M., Singular blocks of restricted $\mathfrak {s}\mathfrak {l}_3$, J. Algebra 471 (2017), 176–192.CrossRefGoogle Scholar
Williamson, G., Schubert calculus and torsion explosion, J. Amer. Math. Soc. 30 (2017), 1023–1046.CrossRefGoogle Scholar
Xi, N., Maximal and primitive elements in Weyl modules for type $A_2$, J. Algebra 215(2) (1999), 735–756.CrossRefGoogle Scholar
Xi, N., Maximal and primitive elements in baby Verma modules for type $B_2$, Representation theory, 257–271, Contemp. Math., 478 (2009)CrossRefGoogle Scholar