Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-23T18:25:16.599Z Has data issue: false hasContentIssue false
  • English
  • Français

Estimates for Convex Integral Means of Harmonic Functions

Published online by Cambridge University Press:  22 November 2013

Dimitrios Betsakos
Dimitrios Betsakos*
Affiliation:
Department of Mathematics, Aristotle University of Thessaloniki, 54124 Thessaloniki, Greece, ([email protected])
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that if f is an integrable function on the unit sphere S in ℝn, g is its symmetric decreasing rearrangement and u, v are the harmonic extensions of f, g in the unit ball 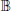, then v has larger convex integral means over each sphere rS, 0 < r < 1, than u has. We also prove that if u is harmonic in 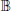with |u| < 1 and u(0) = 0, then the convex integral mean of u on each sphere rS is dominated by that of U, which is the harmonic function with boundary values 1 on the right hemisphere and −1 on the left one.

Keywords

harmonic functionintegral meanssymmetric decreasing rearrangementharmonic measurepolarizationSchwarz lemmaPrimary 31B0531B15
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 57 , Issue 3 , October 2014 , pp. 619 - 630
Copyright
Copyright © Edinburgh Mathematical Society 2014 

References

1.Allen, A. C., Note on a theorem of Gabriel, J. Lond. Math. Soc. 27 (1952), 367–369.CrossRefGoogle Scholar
2.Axler, S., Bourdon, P. and Ramey, W., Harmonic function theory (2nd edn) (Springer, 2001).Google Scholar
3.Baernstein, A. II, Integral means, univalent functions and circular symmetrization, Acta Math. 133 (1974), 139–169.CrossRefGoogle Scholar
4.Baernstein, A. II, Some sharp inequalities for conjugate functions, Indiana Univ. Math. J. 27 (1978), 833–852.Google Scholar
5.Baernstein, A. II and Taylor, B. A., Spherical rearrangements, subharmonic functions, and *-functions in n-space, Duke Math. J. 43 (1976), 245–268.Google Scholar
6.Beardon, A. F., Rhodes, A. D. and Rippon, P. J., Schwarz lemma for harmonic functions, Bull. Hong Kong Math. Soc. 2 (1998), 11–26.Google Scholar
7.Brook, F. and Solynin, A. Yu., An approach to symmetrization via polarization, Trans. Am. Math. Soc. 352 (2000), 1759–1796.CrossRefGoogle Scholar
8.Burokel, R. B., Marshall, D. E., Minda, D., Poggi-Corradini, P. and Rans-Ford, T. J., Area, capacity and diameter versions of Schwarz's lemma, Conform. Geom. Dyn. 12 (2008), 133–152.CrossRefGoogle Scholar
9.Burgeth, B., A Schwarz lemma for harmonic and hyperbolic-harmonic functions in higher dimensions, Manuscr. Math. 77 (1992), 283–291.Google Scholar
10.Duren, P., Harmonic mappings in the plane (Cambridge University Press, 2004).CrossRefGoogle Scholar
11.Essen, M. and Shea, D. F., On some questions of uniqueness in the theory of symmetrization, Annales Acad. Sci. Fenn. A4 (1979), 311–340.Google Scholar
12.Gabriel, R. M., A ‘star inequality’ for harmonic functions, Proc. Lond. Math. Soc. 34 (1932), 305–313.Google Scholar
13.Gariepy, R. and Lewis, J. L., A maximum principle with applications to subharmonic functions in n-space, Ark. Mat. 12 (1974), 253–266.Google Scholar
14.Hayman, W. K. and Kennedy, P. B., Subharmonic functions, Volume 1 (Academic, 1976).Google Scholar
15.Kalaj, D. and Vuorinen, M., On harmonic functions and the Schwarz lemma, Proc. Am. Math. Soc. 140 (2012), 161–165.CrossRefGoogle Scholar
16.Sohwarz, H. A., Gessamelte Mathematische Abhandlungen,> Chelsea Publishing Series (Chelsea, New York, 1972).Google Scholar
17.Solynin, A. Yu., Functional inequalities via polarization, St Petersburg Math. J. 8 (1997), 1015–1038.Google Scholar