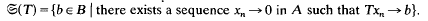Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-11-24T17:27:59.089Z Has data issue: false hasContentIssue false
  • English
  • Français

Discontinuous homomorphisms and the separating space

Published online by Cambridge University Press:  20 January 2009

Niels Grønbaek
Niels Grønbaek
Affiliation:
Matematisk InstitutKøbenhavns Universitet UniversitetsParken 5DK-1200 København ØDenmark
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let T: A → B be a linear operator between two Banach algebras A and B. The basic problem in the theory of automatic continuity is to find algebraic conditions on T, A, and B which ensure that T is continuous. As a means to study continuity properties of T the separating space of T has played a crucial role. It is defined as

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 25 , Issue 1 , February 1982 , pp. 35 - 39
Copyright
Copyright © Edinburgh Mathematical Society 1982

References

REFERENCES

1.Allan, G. R., Embedding the Algebra of Formal Power Series in a Banach Algebra, Proc. London Math. Soc. (3) 25 (1972), 329–340.CrossRefGoogle Scholar
2.Allan, G. R., Elements of Finite Closed Descent in a Banach Algebra, J. London Math. Soc. (2) 7 (1973), 462–466.Google Scholar
3.Badé, W. G., Curtis, P. C. Jr and Laursen, K. B., Divisible Subspaces and Problems of Automatic Continuity, Studia Math. 68 (1980), 159–186.CrossRefGoogle Scholar
4.Grabiner, S., Nilpotency of Banach Nil Algebras, Proc. Amer. Math. Soc. 21 (1969), 510.Google Scholar
5.Johnson, B. E., Continuity of Centralisers on Banach Algebras, J. London Math. Soc. (1) 41 (1966), 639–640.CrossRefGoogle Scholar
6.Sinclair, A. M., Automatic Continuity of Linear Operators (London Math. Soc. Lecture Note Series 21, Cambridge University Press, 1976).CrossRefGoogle Scholar
7.Thomas, M., Algebra Homomorphisms and the Functional Calculus, Pacific J. Math. 79 (1978), 251–269.CrossRefGoogle Scholar
8.Titchmarsh, E. C., The Zeros of Certain Integral Functions, Proc. London Math. Soc. (2) 25 (1926), 283–302.CrossRefGoogle Scholar
9.Varopoulos, N. Th., Sur les formes positives d'une algébre de Banach, C. R. Acad. Sci. Paris 258 (1964), 2465–2467.Google Scholar