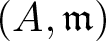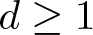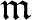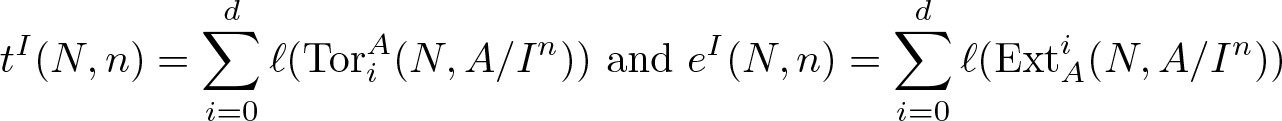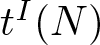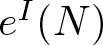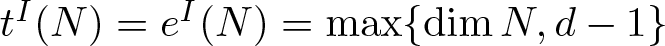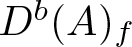1. Introduction
In this paper, all rings considered are commutative, Noetherian, local with unity and all modules considered will be finitely generated. Let ![]() $(A, \mathfrak{m} )$ be a local ring of dimension
$(A, \mathfrak{m} )$ be a local ring of dimension ![]() $d \geq 1$, I an
$d \geq 1$, I an ![]() $\mathfrak{m} $-primary ideal in A and let L be an A-module. If T is an A-module of finite length then we denote by
$\mathfrak{m} $-primary ideal in A and let L be an A-module. If T is an A-module of finite length then we denote by ![]() $\ell(T)$ its length. The Hilbert–Samuel polynomial
$\ell(T)$ its length. The Hilbert–Samuel polynomial ![]() $n \mapsto \ell(L/I^nL)$ of L with respect to I is well-studied. It is known that it is of polynomial type and of degree
$n \mapsto \ell(L/I^nL)$ of L with respect to I is well-studied. It is known that it is of polynomial type and of degree ![]() $\dim L$. Considerably less is known of the function
$\dim L$. Considerably less is known of the function  $n \mapsto \ell(\operatorname{Tor}^A_i(L, A/I^n))$ for
$n \mapsto \ell(\operatorname{Tor}^A_i(L, A/I^n))$ for ![]() $i \geq 1$. It is known that this function is of polynomial type and of degree
$i \geq 1$. It is known that this function is of polynomial type and of degree ![]() $\leq d - 1$. There are some results which show under certain conditions the maximal degree is attained, see [Reference Iyengar and Puthenpurakal2], [Reference Katz and Theodorescu4] and [Reference Puthenpurakal7]. However this function can also be identically zero, see [Reference Puthenpurakal7, Remark 20]. Similarly not much is known of the function
$\leq d - 1$. There are some results which show under certain conditions the maximal degree is attained, see [Reference Iyengar and Puthenpurakal2], [Reference Katz and Theodorescu4] and [Reference Puthenpurakal7]. However this function can also be identically zero, see [Reference Puthenpurakal7, Remark 20]. Similarly not much is known of the function ![]() $n \mapsto \ell(\operatorname{Ext}^i_A(L, A/I^n))$ for
$n \mapsto \ell(\operatorname{Ext}^i_A(L, A/I^n))$ for ![]() $i \geq 1$. It is known that this function is of polynomial type and of degree
$i \geq 1$. It is known that this function is of polynomial type and of degree ![]() $\leq d - 1$. There are some results which show under certain conditions the maximal degree is attained, see [Reference Crabbe, Katz, Striuli and Theodorescu1], [Reference Kadu and Puthenpurakal3]. Even less is known of the functions
$\leq d - 1$. There are some results which show under certain conditions the maximal degree is attained, see [Reference Crabbe, Katz, Striuli and Theodorescu1], [Reference Kadu and Puthenpurakal3]. Even less is known of the functions  $n \mapsto \ell(\operatorname{Tor}^A_i(L, M/I^nM))$ and
$n \mapsto \ell(\operatorname{Tor}^A_i(L, M/I^nM))$ and ![]() $n \mapsto \ell(\operatorname{Ext}_A^i(L, M/I^nM))$ where M is an A-module.
$n \mapsto \ell(\operatorname{Ext}_A^i(L, M/I^nM))$ where M is an A-module.
Perhaps the first case to consider for these functions is when A is regular. In this case, ![]() $\operatorname{projdim} N$ is finite for any A-module N. Surprisingly, we found out that the functions
$\operatorname{projdim} N$ is finite for any A-module N. Surprisingly, we found out that the functions
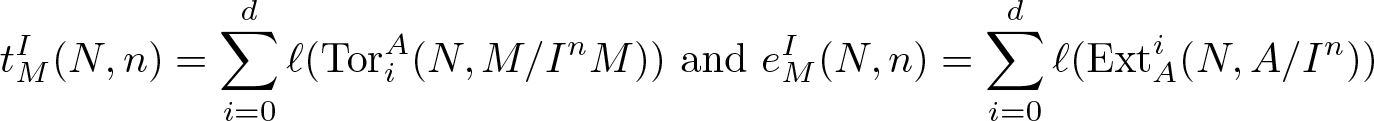 \begin{equation*}
t^I_M(N, n) = \sum_{i = 0}^{d}\ell(\operatorname{Tor}^A_i(N, M/I^nM)) \ \text{and}\ e^I_M(N, n) = \sum_{i = 0}^{d}\ell(\operatorname{Ext}_A^i(N, A/I^n))
\end{equation*}
\begin{equation*}
t^I_M(N, n) = \sum_{i = 0}^{d}\ell(\operatorname{Tor}^A_i(N, M/I^nM)) \ \text{and}\ e^I_M(N, n) = \sum_{i = 0}^{d}\ell(\operatorname{Ext}_A^i(N, A/I^n))
\end{equation*} are easier to tackle. One can then work with ![]() $K^b(\operatorname{proj} A)$, the homotopy category of bounded complexes of projective A-modules, which is the bounded derived category of A. More generally, let
$K^b(\operatorname{proj} A)$, the homotopy category of bounded complexes of projective A-modules, which is the bounded derived category of A. More generally, let ![]() $(A,\mathfrak{m} )$ be a local ring (not necessarily regular). Let
$(A,\mathfrak{m} )$ be a local ring (not necessarily regular). Let ![]() $\mathbf{X}_\bullet \colon \mathbf{X}_\bullet^{-1} \rightarrow \mathbf{X}_\bullet^0 \rightarrow \mathbf{X}_\bullet^{1}$ be a complex of A-modules. In [Reference Theodorescu9, Proposition 3], it is shown that if
$\mathbf{X}_\bullet \colon \mathbf{X}_\bullet^{-1} \rightarrow \mathbf{X}_\bullet^0 \rightarrow \mathbf{X}_\bullet^{1}$ be a complex of A-modules. In [Reference Theodorescu9, Proposition 3], it is shown that if ![]() $\ell(H^0(\mathbf{X}_\bullet\otimes M/I^nM))$ has finite length for all
$\ell(H^0(\mathbf{X}_\bullet\otimes M/I^nM))$ has finite length for all ![]() $n \geq 1$ then the function
$n \geq 1$ then the function ![]() $n \rightarrow \ell(H^0(\mathbf{X}_\bullet\otimes M/I^nM))$ is of polynomial type. The precise degree of this polynomial is difficult to determine (a general upper bound for the degree is given in [Reference Theodorescu9, Proposition 3]).
$n \rightarrow \ell(H^0(\mathbf{X}_\bullet\otimes M/I^nM))$ is of polynomial type. The precise degree of this polynomial is difficult to determine (a general upper bound for the degree is given in [Reference Theodorescu9, Proposition 3]).
1.1. In this paper, we prove a surprising result. Let ![]() $(A, \mathfrak{m} )$ be a local ring and let
$(A, \mathfrak{m} )$ be a local ring and let ![]() $K^b(\operatorname{proj} A)$ be the homotopy category of bounded complexes of projective A-modules, Let
$K^b(\operatorname{proj} A)$ be the homotopy category of bounded complexes of projective A-modules, Let  $K^b_f(\operatorname{proj} A)$ denote the homotopy category of bounded complexes of projective A-modules with finite length cohomology. Let
$K^b_f(\operatorname{proj} A)$ denote the homotopy category of bounded complexes of projective A-modules with finite length cohomology. Let  $\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. We note that for any A-module M and an ideal I we have
$\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. We note that for any A-module M and an ideal I we have ![]() $\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM))$ which has finite length for all
$\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM))$ which has finite length for all ![]() $n \geq 1$ and for all
$n \geq 1$ and for all ![]() $i \in \mathbb{Z} $. The main point of this paper is that it is better to look at the function
$i \in \mathbb{Z} $. The main point of this paper is that it is better to look at the function
 \begin{equation*}
\psi_{\mathbf{X}_\bullet}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*}
\begin{equation*}
\psi_{\mathbf{X}_\bullet}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*} We know that  $\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of polynomial type say of degree
$\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of polynomial type say of degree ![]() $r_I^M(\mathbf{X}_\bullet)$. The main result of this paper is
$r_I^M(\mathbf{X}_\bullet)$. The main result of this paper is
Theorem 1.2. [with hypotheses as in 1.1]
Assume M ≠ 0 and I ≠ A. Then, there exists a nonnegative integer ![]() $r_I^M$ depending only on I and M such if
$r_I^M$ depending only on I and M such if  $\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$ is nonzero then
$\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$ is nonzero then ![]() $r_I^M(\mathbf{X}_\bullet) = r_I^M$.
$r_I^M(\mathbf{X}_\bullet) = r_I^M$.
The essential reason why this happens is because  $K^b_f(\operatorname{proj} A)$ has no proper thick subcategories.
$K^b_f(\operatorname{proj} A)$ has no proper thick subcategories.
1.3. Thus, to determine ![]() $r_I^M(X)$, it suffices to compute it for a single nonzero complex
$r_I^M(X)$, it suffices to compute it for a single nonzero complex ![]() $\mathbf{X}_\bullet$ in
$\mathbf{X}_\bullet$ in  $K^b_f(\operatorname{proj} A)$. As a consequence of Theorem 1.2, we show
$K^b_f(\operatorname{proj} A)$. As a consequence of Theorem 1.2, we show
Theorem 1.4. [with hypotheses as in Theorem 1.2]
If ![]() $\dim M \gt 0$ and I is
$\dim M \gt 0$ and I is ![]() $\mathfrak{m} $-primary then
$\mathfrak{m} $-primary then ![]() $r_I^M = \dim M - 1$.
$r_I^M = \dim M - 1$.
1.5. Let A be a Cohen–Macaulay local ring. Let I ≠ A be an ideal of A and let M be a nonzero A-module. If L is a nonzero module of finite length and finite projective dimension, set ![]() $t^I_M(L, n)$ and
$t^I_M(L, n)$ and ![]() $e^I_M(L, n)$ as before. Also let
$e^I_M(L, n)$ as before. Also let ![]() $t^I_M(L)$ and
$t^I_M(L)$ and ![]() $e^I_M(L)$ denote the degree of the corresponding functions of polynomial type. We show
$e^I_M(L)$ denote the degree of the corresponding functions of polynomial type. We show
Corollary 1.6. (with hypotheses as in 1.5)
Let ![]() $L_1, L_2$ be two nonzero modules of finite length and finite projective dimension. Then
$L_1, L_2$ be two nonzero modules of finite length and finite projective dimension. Then
1.7. We now consider the case when ![]() $\dim M \gt 0$ and I is
$\dim M \gt 0$ and I is ![]() $\mathfrak{m} $-primary. Let
$\mathfrak{m} $-primary. Let ![]() $\mathbf{X}_\bullet \in K^b(\operatorname{proj} A)$. Then by [Reference Theodorescu9, Proposition 3], it follows that
$\mathbf{X}_\bullet \in K^b(\operatorname{proj} A)$. Then by [Reference Theodorescu9, Proposition 3], it follows that  $\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of degree
$\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of degree
Furthermore if ![]() $\dim H^*(\mathbf{X}_\bullet\otimes M) \geq \dim M$ then
$\dim H^*(\mathbf{X}_\bullet\otimes M) \geq \dim M$ then ![]() $s_I^M(\mathbf{X}_\bullet) = \dim H^*(\mathbf{X}_\bullet \otimes M)$. We prove
$s_I^M(\mathbf{X}_\bullet) = \dim H^*(\mathbf{X}_\bullet \otimes M)$. We prove
Theorem 1.8. (with hypotheses as in 1.7)
We have
1.9. Let I ≠ A be an ![]() $\mathfrak{m} $-primary ideal of A and let M be a A-module with
$\mathfrak{m} $-primary ideal of A and let M be a A-module with ![]() $\dim M \gt 0$. If L is a nonzero module of finite projective dimension, set
$\dim M \gt 0$. If L is a nonzero module of finite projective dimension, set ![]() $t^I_M(L, n) \ \text{and}\ e^I_M(L, n)$ as before. Also let
$t^I_M(L, n) \ \text{and}\ e^I_M(L, n)$ as before. Also let ![]() $t^I_M(L)$ and
$t^I_M(L)$ and ![]() $e^I_M(L)$ denote the degree of the corresponding functions of polynomial type. As an application of Theorem 1.8, we have
$e^I_M(L)$ denote the degree of the corresponding functions of polynomial type. As an application of Theorem 1.8, we have
Corollary 1.10. (with hypotheses as in 1.9)
We have
As an application of this corollary (with N = L and M = A), we get the result stated in the abstract.
We now describe in brief the contents of this paper. In § 2, we discuss a few preliminary results. In § 3, we prove Theorem 1.2 and Corollary 1.6. In § 4, we give a proof of Theorem 1.4. In § 5, we give a proof of Theorem 1.8. Finally, in § 6, we give a proof of Corollary 1.10.
2. Preliminaries
In this section, we discuss a few preliminary results that we need. We use [Reference Neeman6] for notation on triangulated categories. However, we will assume that if ![]() $\mathcal{C}$ is a triangulated category then
$\mathcal{C}$ is a triangulated category then ![]() $\operatorname{Hom}_\mathcal{C}(X, Y)$ is a set for any objects
$\operatorname{Hom}_\mathcal{C}(X, Y)$ is a set for any objects ![]() $X, Y$ of
$X, Y$ of ![]() $\mathcal{C}$.
$\mathcal{C}$.
2.1. Let ![]() $\mathcal{C} $ be an essentially small triangulated category with shift operator Σ and let
$\mathcal{C} $ be an essentially small triangulated category with shift operator Σ and let ![]() $\operatorname{Iso}(\mathcal{C} )$ be the set of isomorphism classes of objects in
$\operatorname{Iso}(\mathcal{C} )$ be the set of isomorphism classes of objects in ![]() $\mathcal{C} $. By a weak triangle function on
$\mathcal{C} $. By a weak triangle function on ![]() $\mathcal{C} $, we mean a function
$\mathcal{C} $, we mean a function ![]() $\xi \colon \operatorname{Iso}(\mathcal{C} ) \rightarrow \mathbb{Z} $ suchthat
$\xi \colon \operatorname{Iso}(\mathcal{C} ) \rightarrow \mathbb{Z} $ suchthat
(1)
 $\xi(X) \geq 0$ for all
$\xi(X) \geq 0$ for all  $X \in \mathcal{C} $.
$X \in \mathcal{C} $.(2)
 $\xi(0) = 0$.
$\xi(0) = 0$.(3)
 $\xi(X \oplus Y) = \xi(X) + \xi(Y)$ for all
$\xi(X \oplus Y) = \xi(X) + \xi(Y)$ for all  $X, Y \in \mathcal{C} $.
$X, Y \in \mathcal{C} $.(4)
 $\xi(\Sigma X ) = \xi(X)$ for all
$\xi(\Sigma X ) = \xi(X)$ for all  $X \in \mathcal{C} $.
$X \in \mathcal{C} $.(5) If
 $X \rightarrow Y \rightarrow Z \rightarrow \Sigma X $ is a triangle in
$X \rightarrow Y \rightarrow Z \rightarrow \Sigma X $ is a triangle in  $\mathcal{C} $ then
$\mathcal{C} $ then  $\xi(Z) \leq \xi(X) + \xi(Y)$.
$\xi(Z) \leq \xi(X) + \xi(Y)$.
2.2. Set
The following result (essentially an observation) is a crucial ingredient in our proof of Theorem 1.2.
Lemma 2.3. (with hypotheses as above)
![]() $\ker \xi $ is a thick subcategory of
$\ker \xi $ is a thick subcategory of ![]() $\mathcal{C} $.
$\mathcal{C} $.
Proof. We have
(1)
 $0 \in \ker \xi$.
$0 \in \ker \xi$.(2) If
 $X \cong Y$ and
$X \cong Y$ and  $X \in \ker \xi$. Then note
$X \in \ker \xi$. Then note  $\xi(Y) = \xi(X) = 0$. So
$\xi(Y) = \xi(X) = 0$. So  $Y \in \ker \xi$.
$Y \in \ker \xi$.(3) If
 $X \in \ker \xi$ then note
$X \in \ker \xi$ then note  $\xi(\Sigma X) = \xi(X) = 0$. So
$\xi(\Sigma X) = \xi(X) = 0$. So  $\Sigma X \in \ker \xi$. Similarly
$\Sigma X \in \ker \xi$. Similarly  $\Sigma^{-1} X \in \ker \xi$.
$\Sigma^{-1} X \in \ker \xi$.(4) If
 $X \rightarrow Y \rightarrow Z \rightarrow \Sigma X$ is a triangle in
$X \rightarrow Y \rightarrow Z \rightarrow \Sigma X$ is a triangle in  $\mathcal{C} $ with
$\mathcal{C} $ with  $X, Y \in \ker \xi$. Then note
$X, Y \in \ker \xi$. Then note
 \begin{equation*}
0 \leq \xi(Z) \leq \xi(X) + \xi(Y) = 0 + 0 = 0.
\end{equation*}
\begin{equation*}
0 \leq \xi(Z) \leq \xi(X) + \xi(Y) = 0 + 0 = 0.
\end{equation*}So
 $Z \in \ker \xi$.
$Z \in \ker \xi$.(5) If
 $X \oplus Y \in \ker \xi$ then
$X \oplus Y \in \ker \xi$ then  $\xi(X) + \xi(Y) = \xi(X \oplus Y) = 0$. As
$\xi(X) + \xi(Y) = \xi(X \oplus Y) = 0$. As  $\xi(X), \xi(Y)$ are nonnegative, it follows that
$\xi(X), \xi(Y)$ are nonnegative, it follows that  $\xi(X) = \xi(Y) = 0$. Thus
$\xi(X) = \xi(Y) = 0$. Thus  $X, Y \in \ker \xi$.
$X, Y \in \ker \xi$.
It follows that ![]() $\ker \xi$ is a thick subcategory of
$\ker \xi$ is a thick subcategory of ![]() $\mathcal{C} $.
$\mathcal{C} $.
2.4. Let A be a ring. Let ![]() $K^b(\operatorname{proj} A)$ be the homotopy category of bounded complexes of projective complexes. We index complexes cohomologically,
$K^b(\operatorname{proj} A)$ be the homotopy category of bounded complexes of projective complexes. We index complexes cohomologically,
We note that ![]() $\mathbf{X}_\bullet = 0$ in
$\mathbf{X}_\bullet = 0$ in ![]() $K^b(\operatorname{proj} A)$ if and only if
$K^b(\operatorname{proj} A)$ if and only if ![]() $H^*(\mathbf{X}_\bullet) = 0$. If
$H^*(\mathbf{X}_\bullet) = 0$. If ![]() $\mathbf{X}_\bullet = 0$ in
$\mathbf{X}_\bullet = 0$ in ![]() $K^b(\operatorname{proj} A)$ then note that
$K^b(\operatorname{proj} A)$ then note that ![]() $H^*(X\otimes N) = 0$ for any A-module N.
$H^*(X\otimes N) = 0$ for any A-module N.
2.5. Let  $K^b_f(\operatorname{proj} A)$ denote the homotopy category of bounded complexes of projective complexes with finite length cohomology. We note that if
$K^b_f(\operatorname{proj} A)$ denote the homotopy category of bounded complexes of projective complexes with finite length cohomology. We note that if  $\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$ and N is an A-module then
$\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$ and N is an A-module then ![]() $H^*(\mathbf{X}_\bullet \otimes N)$ also has finite length. To see this if P is a prime ideal in A with
$H^*(\mathbf{X}_\bullet \otimes N)$ also has finite length. To see this if P is a prime ideal in A with ![]() $P \neq \mathfrak{m} $ then
$P \neq \mathfrak{m} $ then
 \begin{equation*}
H^*(\mathbf{X}_\bullet \otimes_A N)_P = H^*({\mathbf{X}_\bullet}_P \otimes_{A_P} N_P) = 0 \quad \text{as ${\mathbf{X}_\bullet}_P = 0$ in $K^b(\operatorname{proj} A_P)$}.
\end{equation*}
\begin{equation*}
H^*(\mathbf{X}_\bullet \otimes_A N)_P = H^*({\mathbf{X}_\bullet}_P \otimes_{A_P} N_P) = 0 \quad \text{as ${\mathbf{X}_\bullet}_P = 0$ in $K^b(\operatorname{proj} A_P)$}.
\end{equation*}Lemma 2.6. Let ![]() $\mathbf{X}_\bullet \in K^b(\operatorname{proj} A)$ be nonzero. Let N ≠ 0. Then
$\mathbf{X}_\bullet \in K^b(\operatorname{proj} A)$ be nonzero. Let N ≠ 0. Then ![]() $H^*(\mathbf{X}_\bullet \otimes N) \neq 0$.
$H^*(\mathbf{X}_\bullet \otimes N) \neq 0$.
Proof. We may assume ![]() $\mathbf{X}_\bullet$ is a minimal complex. Furthermore (after a shift), we may assume that
$\mathbf{X}_\bullet$ is a minimal complex. Furthermore (after a shift), we may assume that ![]() $\mathbf{X}_\bullet^0 \neq 0$ and
$\mathbf{X}_\bullet^0 \neq 0$ and ![]() $\mathbf{X}_\bullet^i = 0$ for
$\mathbf{X}_\bullet^i = 0$ for ![]() $i \geq 1$. Let
$i \geq 1$. Let ![]() $H^0(\mathbf{X}_\bullet) = E \neq 0$ since
$H^0(\mathbf{X}_\bullet) = E \neq 0$ since ![]() $\mathbf{X}_\bullet$ is minimal. It is straight forward to check that
$\mathbf{X}_\bullet$ is minimal. It is straight forward to check that ![]() $H^0(\mathbf{X}_\bullet \otimes N) = E\otimes N \neq 0$. The result follows.
$H^0(\mathbf{X}_\bullet \otimes N) = E\otimes N \neq 0$. The result follows.
2.7. Suppose for an A-module M and an ideal I we have ![]() $\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM))$ has finite length for all
$\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM))$ has finite length for all ![]() $n \geq 1$ and for all
$n \geq 1$ and for all ![]() $i \in \mathbb{Z} $. Consider the function
$i \in \mathbb{Z} $. Consider the function
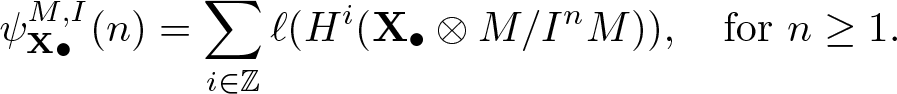 \begin{equation*}
\psi_{\mathbf{X}_\bullet}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*}
\begin{equation*}
\psi_{\mathbf{X}_\bullet}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell(H^i(\mathbf{X}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*} By [Reference Theodorescu9, Proposition 3] we know that  $\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of polynomial type say of degree
$\psi_{\mathbf{X}_\bullet}^{M, I}(n)$ is of polynomial type say of degree ![]() $r_I^M(X)$ and
$r_I^M(X)$ and
2.8. Let I be an ![]() $\mathfrak{m} $-primary ideal in A and let M be an A-module. An element
$\mathfrak{m} $-primary ideal in A and let M be an A-module. An element ![]() $x \in I$ is said to be M-superficial with respect to I if there exists c such that
$x \in I$ is said to be M-superficial with respect to I if there exists c such that ![]() $(I^{n+1}M \colon x) \cap I^cM = I^nM$ for all
$(I^{n+1}M \colon x) \cap I^cM = I^nM$ for all ![]() $n \gg 0$. Superficial elements exist when
$n \gg 0$. Superficial elements exist when ![]() $k = A/\mathfrak{m} $ is infinite, (see [Reference Sally8, p. 7] for the case when M = A; the same proof generalizes).
$k = A/\mathfrak{m} $ is infinite, (see [Reference Sally8, p. 7] for the case when M = A; the same proof generalizes).
2.9. If ![]() $\operatorname{grade}(I, M) \gt 0$ and x is M-superficial with respect to I then x is M-regular. This fact is well-known. We give a proof due to lack of a suitable reference. Let
$\operatorname{grade}(I, M) \gt 0$ and x is M-superficial with respect to I then x is M-regular. This fact is well-known. We give a proof due to lack of a suitable reference. Let ![]() $(I^{n+1}M \colon x) \cap I^cM = I^nM$ for all
$(I^{n+1}M \colon x) \cap I^cM = I^nM$ for all ![]() $n \gg 0$. Let
$n \gg 0$. Let ![]() $u \in I$ be M-regular. If xm = 0 then
$u \in I$ be M-regular. If xm = 0 then ![]() $xu^cm = 0$. So
$xu^cm = 0$. So ![]() $u^cm \in I^n$ for all
$u^cm \in I^n$ for all ![]() $n \gg 0$. Thus
$n \gg 0$. Thus ![]() $u^cm = 0$ and so m = 0.
$u^cm = 0$ and so m = 0.
2.10. A sequence ![]() $\mathbf{x} = x_1, \ldots, x_r \in M$ is said to be an M-superficial sequence if xi is
$\mathbf{x} = x_1, \ldots, x_r \in M$ is said to be an M-superficial sequence if xi is ![]() $M/(x_1, \ldots, x_{i-1})M$-superficial for
$M/(x_1, \ldots, x_{i-1})M$-superficial for ![]() $i = 1, \ldots, r$. If
$i = 1, \ldots, r$. If ![]() $\operatorname{grade}(I, M) \geq r$ then it follows from 2.9 that x is an A-regular sequence.
$\operatorname{grade}(I, M) \geq r$ then it follows from 2.9 that x is an A-regular sequence.
3. Proof of Theorem 1.2 and Corollary 1.6
In this section, we give proofs of Theorem 1.2 and Corollary 1.6. We first give
Proof of Theorem 1.2
By 2.6, it follows that the function  $\psi_{\mathbf{X}_\bullet}^{M, I}(n) \neq 0$ for all
$\psi_{\mathbf{X}_\bullet}^{M, I}(n) \neq 0$ for all ![]() $n \geq 1$. Thus
$n \geq 1$. Thus ![]() $r_I^M(\mathbf{X}_\bullet) \geq 0$ for all
$r_I^M(\mathbf{X}_\bullet) \geq 0$ for all ![]() $\mathbf{X}_\bullet \neq 0$. Also by 2.7,
$\mathbf{X}_\bullet \neq 0$. Also by 2.7, ![]() $r_I^M(\mathbf{X}_\bullet) \leq \dim A$ for any
$r_I^M(\mathbf{X}_\bullet) \leq \dim A$ for any  $\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. Let
$\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. Let
For ![]() $\mathbf{Y}_\bullet \in K^b(\operatorname{proj} A)_f$ define
$\mathbf{Y}_\bullet \in K^b(\operatorname{proj} A)_f$ define
 \begin{equation*}\eta(\mathbf{Y}_\bullet) = \lim_{n \rightarrow \infty} \frac{c!}{n^c} \psi_{\mathbf{Y}_\bullet}^{M, I}(n). \end{equation*}
\begin{equation*}\eta(\mathbf{Y}_\bullet) = \lim_{n \rightarrow \infty} \frac{c!}{n^c} \psi_{\mathbf{Y}_\bullet}^{M, I}(n). \end{equation*} Clearly ![]() $\eta(\mathbf{Y}_\bullet) \in \mathbb{Z} _{\geq 0}$. Furthermore if
$\eta(\mathbf{Y}_\bullet) \in \mathbb{Z} _{\geq 0}$. Furthermore if ![]() $\mathbf{Y}_\bullet \cong \mathbf{Z}_\bullet$ then clearly
$\mathbf{Y}_\bullet \cong \mathbf{Z}_\bullet$ then clearly ![]() $\eta(\mathbf{Y}_\bullet) = \eta(\mathbf{Z}_\bullet)$. Thus, we have a function
$\eta(\mathbf{Y}_\bullet) = \eta(\mathbf{Z}_\bullet)$. Thus, we have a function  $\eta \colon \operatorname{Iso}(K^b_f(\operatorname{proj} A)) \rightarrow \mathbb{Z} $ where
$\eta \colon \operatorname{Iso}(K^b_f(\operatorname{proj} A)) \rightarrow \mathbb{Z} $ where  $\operatorname{Iso}(K^b_f(\operatorname{proj} A))$ denotes the set of isomorphism classes of objects in
$\operatorname{Iso}(K^b_f(\operatorname{proj} A))$ denotes the set of isomorphism classes of objects in  $K^b_f(\operatorname{proj} A)$.
$K^b_f(\operatorname{proj} A)$.
Claim: η is a weak triangle function on  $K^b_f(\operatorname{proj} A)$.
$K^b_f(\operatorname{proj} A)$.
Assume the claim for the time-being. By 2.3, ![]() $\ker \eta$ is a thick subcategory of
$\ker \eta$ is a thick subcategory of  $K^b_f(\operatorname{proj} A)$. Let
$K^b_f(\operatorname{proj} A)$. Let ![]() $\mathbf{X}_\bullet$ be such that
$\mathbf{X}_\bullet$ be such that ![]() $r_I^M(\mathbf{X}_\bullet) = c$. Then
$r_I^M(\mathbf{X}_\bullet) = c$. Then ![]() $\eta(\mathbf{X}_\bullet) \gt 0$. So
$\eta(\mathbf{X}_\bullet) \gt 0$. So ![]() $\mathbf{X}_\bullet \notin \ker \eta$. Thus
$\mathbf{X}_\bullet \notin \ker \eta$. Thus ![]() $\ker \eta \neq K^b(\operatorname{proj} A)$. By [Reference Neeman5, Lemma 1.2], it follows that
$\ker \eta \neq K^b(\operatorname{proj} A)$. By [Reference Neeman5, Lemma 1.2], it follows that ![]() $\ker \eta = 0$. Thus
$\ker \eta = 0$. Thus ![]() $r_I^M(\mathbf{Y}_\bullet) = c$ for any
$r_I^M(\mathbf{Y}_\bullet) = c$ for any ![]() $\mathbf{Y}_\bullet \neq 0$ in
$\mathbf{Y}_\bullet \neq 0$ in  $K^b_f(\operatorname{proj} A)$.
$K^b_f(\operatorname{proj} A)$.
It remains to prove the claim. The first four properties of definition in 2.1 are trivial to verify. Let  $\mathbf{X}_\bullet \xrightarrow{f} \mathbf{Y}_\bullet \rightarrow \mathbf{Z}_\bullet \rightarrow \mathbf{X}_\bullet[1]$ be a triangle in
$\mathbf{X}_\bullet \xrightarrow{f} \mathbf{Y}_\bullet \rightarrow \mathbf{Z}_\bullet \rightarrow \mathbf{X}_\bullet[1]$ be a triangle in  $K^b_f(\operatorname{proj} A)$. Then
$K^b_f(\operatorname{proj} A)$. Then ![]() $\mathbf{Z}_\bullet \cong \operatorname{cone}(f)$ and we have an exact sequence in
$\mathbf{Z}_\bullet \cong \operatorname{cone}(f)$ and we have an exact sequence in ![]() $C^b(\operatorname{proj} A)$
$C^b(\operatorname{proj} A)$
As ![]() $\mathbf{X}_\bullet^i$ are free A-modules we have an exact sequence for all
$\mathbf{X}_\bullet^i$ are free A-modules we have an exact sequence for all ![]() $n \geq 1$,
$n \geq 1$,
Taking homology we have
 \begin{equation*}
\psi_{\mathbf{Z}_\bullet}^{M, I}(n) \leq \psi_{\mathbf{Y}_\bullet}^{M, I}(n) + \psi_{\mathbf{X}_\bullet[1]}^{M, I}(n)
\end{equation*}
\begin{equation*}
\psi_{\mathbf{Z}_\bullet}^{M, I}(n) \leq \psi_{\mathbf{Y}_\bullet}^{M, I}(n) + \psi_{\mathbf{X}_\bullet[1]}^{M, I}(n)
\end{equation*} for all ![]() $n \geq 1$. It follows that
$n \geq 1$. It follows that
Thus, η is a weak triangle function on  $K^b_f(\operatorname{proj} A)$.
$K^b_f(\operatorname{proj} A)$.
Next we give
Proof of Corollary 1.6
By Theorem 1.2, we have that there exists c with ![]() $r_I^M(\mathbf{X}_\bullet) = c$ for any nonzero
$r_I^M(\mathbf{X}_\bullet) = c$ for any nonzero  $\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. Let L be a nonzero finite length A-module with finite projective dimension. Let
$\mathbf{X}_\bullet \in K^b_f(\operatorname{proj} A)$. Let L be a nonzero finite length A-module with finite projective dimension. Let ![]() $\mathbf{Y}_\bullet$ be a minimal projective resolution of L. Then
$\mathbf{Y}_\bullet$ be a minimal projective resolution of L. Then  $\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ and is nonzero. It follows that
$\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ and is nonzero. It follows that ![]() $r_I^M(\mathbf{Y}_\bullet) = c$. Observe that
$r_I^M(\mathbf{Y}_\bullet) = c$. Observe that ![]() $r_I^M(\mathbf{Y}_\bullet) = t^I_M(L)$. Set
$r_I^M(\mathbf{Y}_\bullet) = t^I_M(L)$. Set ![]() $\mathbf{Y}_\bullet^* = \operatorname{Hom}_A(\mathbf{Y}_\bullet, A)$. Note that
$\mathbf{Y}_\bullet^* = \operatorname{Hom}_A(\mathbf{Y}_\bullet, A)$. Note that  $\mathbf{Y}_\bullet^* \in K^b_f(A)$ and is nonzero. Also observe
$\mathbf{Y}_\bullet^* \in K^b_f(A)$ and is nonzero. Also observe
Therefore
The result follows.
4. Proof of Theorem 1.4
In this section, we assume ![]() $(A, \mathfrak{m} )$ is local ring, M is an A-module with
$(A, \mathfrak{m} )$ is local ring, M is an A-module with ![]() $\dim M \gt 0$ and I is an
$\dim M \gt 0$ and I is an ![]() $\mathfrak{m} $-primary ideal. In this section, we give a proof of Theorem 1.4. We first discuss the invariant
$\mathfrak{m} $-primary ideal. In this section, we give a proof of Theorem 1.4. We first discuss the invariant ![]() $r_I^M(A)$ under base change.
$r_I^M(A)$ under base change.
4.1. Base change:
(1) We first consider a flat base change ![]() $A \rightarrow B$ where
$A \rightarrow B$ where ![]() $(B, \mathfrak{n} )$ is local and
$(B, \mathfrak{n} )$ is local and ![]() $\mathfrak{n} = \mathfrak{m} B$. We claim that
$\mathfrak{n} = \mathfrak{m} B$. We claim that  $r_I^M(A) = r_{IB}^{M\otimes_A B}(B)$.
$r_I^M(A) = r_{IB}^{M\otimes_A B}(B)$.
In this case, we first observe that if E is an A-module of finite length then ![]() $\ell_B(E\otimes_A B) = \ell_A(E)$. Also if
$\ell_B(E\otimes_A B) = \ell_A(E)$. Also if ![]() $\mathbf{X}_\bullet $ is a bounded complex of A-modules with finite length cohomology then
$\mathbf{X}_\bullet $ is a bounded complex of A-modules with finite length cohomology then ![]() $\mathbf{X}_\bullet\otimes_A B$ is a bounded complex of B-modules with finite length cohomology and
$\mathbf{X}_\bullet\otimes_A B$ is a bounded complex of B-modules with finite length cohomology and ![]() $\ell_B(H^*(\mathbf{X}_\bullet\otimes B)) = \ell_A(H^*(\mathbf{X}_\bullet))$. If
$\ell_B(H^*(\mathbf{X}_\bullet\otimes B)) = \ell_A(H^*(\mathbf{X}_\bullet))$. If  $\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ then
$\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ then  $\mathbf{Y}_\bullet \otimes_A B \in K^b_f(\operatorname{proj} B)$. Let
$\mathbf{Y}_\bullet \otimes_A B \in K^b_f(\operatorname{proj} B)$. Let  $\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ be nonzero. Set
$\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} A)$ be nonzero. Set
 \begin{equation*}
\psi_{\mathbf{Y}_\bullet, A}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{Y}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*}
\begin{equation*}
\psi_{\mathbf{Y}_\bullet, A}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{Y}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}.
\end{equation*}Then
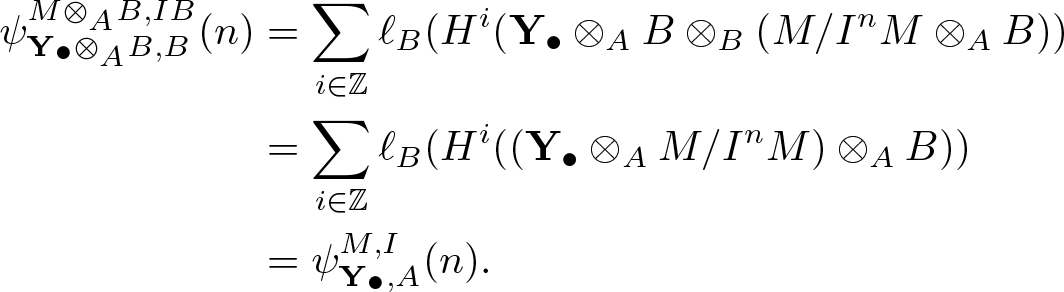 \begin{align*}
\psi_{\mathbf{Y}_\bullet\otimes_A B, B}^{M\otimes_A B, IB}(n) &= \sum_{i \in \mathbb{Z} }\ell_B(H^i(\mathbf{Y}_\bullet \otimes_A B \otimes_B (M/I^nM \otimes_A B)) \\
&= \sum_{i \in \mathbb{Z} }\ell_B(H^i((\mathbf{Y}_\bullet \otimes_A M/I^nM) \otimes_A B)) \\
&= \psi_{\mathbf{Y}_\bullet, A}^{M, I}(n).
\end{align*}
\begin{align*}
\psi_{\mathbf{Y}_\bullet\otimes_A B, B}^{M\otimes_A B, IB}(n) &= \sum_{i \in \mathbb{Z} }\ell_B(H^i(\mathbf{Y}_\bullet \otimes_A B \otimes_B (M/I^nM \otimes_A B)) \\
&= \sum_{i \in \mathbb{Z} }\ell_B(H^i((\mathbf{Y}_\bullet \otimes_A M/I^nM) \otimes_A B)) \\
&= \psi_{\mathbf{Y}_\bullet, A}^{M, I}(n).
\end{align*} It follows that degree of the function  $\psi_{\mathbf{Y}_\bullet, A}^{M, I}(n)$ is equal to degree of
$\psi_{\mathbf{Y}_\bullet, A}^{M, I}(n)$ is equal to degree of  $\psi_{\mathbf{Y}_\bullet\otimes_A B, B}^{M\otimes_A B, IB}(n)$. The result follows.
$\psi_{\mathbf{Y}_\bullet\otimes_A B, B}^{M\otimes_A B, IB}(n)$. The result follows.
(2) If ![]() $(Q, \mathfrak{n} ) \rightarrow (A, \mathfrak{m} )$ is a surjective ring homomorphism and if J is any
$(Q, \mathfrak{n} ) \rightarrow (A, \mathfrak{m} )$ is a surjective ring homomorphism and if J is any ![]() $\mathfrak{n} $-primary ideal in Q with JA = I then
$\mathfrak{n} $-primary ideal in Q with JA = I then ![]() $r_I^M(A) = r_J^M(Q)$. To see this, if
$r_I^M(A) = r_J^M(Q)$. To see this, if  $\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} Q)$ then
$\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} Q)$ then  $\mathbf{Y}_\bullet \otimes_Q A \in K^b_f(\operatorname{proj} A)$. Let
$\mathbf{Y}_\bullet \otimes_Q A \in K^b_f(\operatorname{proj} A)$. Let  $\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} Q)$ be nonzero. Set
$\mathbf{Y}_\bullet \in K^b_f(\operatorname{proj} Q)$ be nonzero. Set
 \begin{equation*}
\psi_{\mathbf{Y}_\bullet, Q}^{M, J}(n) = \sum_{i \in \mathbb{Z} }\ell_Q(H^i(\mathbf{Y}_\bullet \otimes_QM/J^nM), \quad \text{for $n \geq 1$}.
\end{equation*}
\begin{equation*}
\psi_{\mathbf{Y}_\bullet, Q}^{M, J}(n) = \sum_{i \in \mathbb{Z} }\ell_Q(H^i(\mathbf{Y}_\bullet \otimes_QM/J^nM), \quad \text{for $n \geq 1$}.
\end{equation*}Then
 \begin{align*}
\psi_{\mathbf{Y}_\bullet\otimes_Q A, A}^{M, I}(n) &= \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{Y}_\bullet \otimes_Q A \otimes_A M/I^nM ) \\
&= \sum_{i \in \mathbb{Z} }\ell_Q(H^i((\mathbf{Y}_\bullet\otimes_Q M/J^nM ) \\
&= \psi_{\mathbf{Y}_\bullet, Q}^{M, J}(n).
\end{align*}
\begin{align*}
\psi_{\mathbf{Y}_\bullet\otimes_Q A, A}^{M, I}(n) &= \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{Y}_\bullet \otimes_Q A \otimes_A M/I^nM ) \\
&= \sum_{i \in \mathbb{Z} }\ell_Q(H^i((\mathbf{Y}_\bullet\otimes_Q M/J^nM ) \\
&= \psi_{\mathbf{Y}_\bullet, Q}^{M, J}(n).
\end{align*}The result follows.
(3) If ![]() $\mathfrak{q} \subseteq \operatorname{ann}_A M$ then note that M can be considered as a
$\mathfrak{q} \subseteq \operatorname{ann}_A M$ then note that M can be considered as a ![]() $C = A/\mathfrak{q} $-module. Set
$C = A/\mathfrak{q} $-module. Set ![]() $J = (I+ \mathfrak{q} /\mathfrak{q} )$. Note J is primary to the maximal ideal of C. Then
$J = (I+ \mathfrak{q} /\mathfrak{q} )$. Note J is primary to the maximal ideal of C. Then ![]() $r_I^M = r_J^M$. The proof of this assertion is similar to (2).
$r_I^M = r_J^M$. The proof of this assertion is similar to (2).
We now give
Proof of Theorem 1.4
By 1.7, we have ![]() $r_I^M \leq \dim M -1$. We first do the following base-changes:
$r_I^M \leq \dim M -1$. We first do the following base-changes:
(1) If the residue field of A is finite then we set
 $B = A[X]_{\mathfrak{m} A[X]}$ then
$B = A[X]_{\mathfrak{m} A[X]}$ then  $(B,\mathfrak{n} )$ is a flat extension of A with
$(B,\mathfrak{n} )$ is a flat extension of A with  $\mathfrak{m} B = \mathfrak{n} $ and the residue field of B is k(X) is infinite. So we replace M by
$\mathfrak{m} B = \mathfrak{n} $ and the residue field of B is k(X) is infinite. So we replace M by  $M \otimes_A B$ and I by IB (see 4.1(1)).
$M \otimes_A B$ and I by IB (see 4.1(1)).(2) We then complete A (see 4.1(1)).
(3) By (1), (2) we assume A is complete with an infinite residue field. Let A be a quotient of a regular local ring Q. Then, we can replace A by Q (see 4.1(2)).
(4) By (3), we can assume A is regular local with infinite residue field. We note
 $a = \operatorname{grade}(\operatorname{ann} M) = \operatorname{height} \operatorname{ann} M$. Choose
$a = \operatorname{grade}(\operatorname{ann} M) = \operatorname{height} \operatorname{ann} M$. Choose  $y_1, \ldots, y_a \in
\operatorname{ann} M $ an A-regular sequence. By 4.1(3), we can replace A with
$y_1, \ldots, y_a \in
\operatorname{ann} M $ an A-regular sequence. By 4.1(3), we can replace A with  $A/(y_1,\ldots, y_a)$.
$A/(y_1,\ldots, y_a)$.
Thus, we can assume A is Cohen–Macaulay with infinite residue field and ![]() $\dim A = \dim M \gt 0$. Let
$\dim A = \dim M \gt 0$. Let ![]() $d = \dim A$ and let
$d = \dim A$ and let ![]() $\mathbf{x} = x_1, \ldots, x_d$ be a maximal
$\mathbf{x} = x_1, \ldots, x_d$ be a maximal ![]() $M \oplus A$-superficial sequence with respect to I. Then as x is an A-superficial sequence with respect to I it is an A-regular sequence, see 2.10. Let
$M \oplus A$-superficial sequence with respect to I. Then as x is an A-superficial sequence with respect to I it is an A-regular sequence, see 2.10. Let ![]() $\mathbf{K}_\bullet$ be the Koszul complex on x. Then
$\mathbf{K}_\bullet$ be the Koszul complex on x. Then  $\mathbf{K}_\bullet \in K^b_f(\operatorname{proj} A)$. We also note that as x 1 is M-superficial with respect to I there exists c and n 0 such that
$\mathbf{K}_\bullet \in K^b_f(\operatorname{proj} A)$. We also note that as x 1 is M-superficial with respect to I there exists c and n 0 such that ![]() $(I^{n}M \colon x_1)\cap I^cM = I^{n-1}M$ for all
$(I^{n}M \colon x_1)\cap I^cM = I^{n-1}M$ for all ![]() $n \geq n_0$.
$n \geq n_0$.
Set
 \begin{equation*}
\psi_{\mathbf{K}_\bullet, A}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{K}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}
\end{equation*}
\begin{equation*}
\psi_{\mathbf{K}_\bullet, A}^{M, I}(n) = \sum_{i \in \mathbb{Z} }\ell_A(H^i(\mathbf{K}_\bullet \otimes M/I^nM)), \quad \text{for $n \geq 1$}
\end{equation*}
and let r be its degree. By 2.7, ![]() $r \leq d - 1$. We note that
$r \leq d - 1$. We note that
 \begin{equation*}
H^d(\mathbf{K}_\bullet \otimes M/I^nM) = \frac{I^nM \colon \mathbf{x} }{I^nM} \supseteq \frac{(I^nM \colon \mathbf{x} )\cap I^cM}{I^nM} = \frac{I^{n-1}M}{I^nM} \ (\text{for } n \geq n_0).
\end{equation*}
\begin{equation*}
H^d(\mathbf{K}_\bullet \otimes M/I^nM) = \frac{I^nM \colon \mathbf{x} }{I^nM} \supseteq \frac{(I^nM \colon \mathbf{x} )\cap I^cM}{I^nM} = \frac{I^{n-1}M}{I^nM} \ (\text{for } n \geq n_0).
\end{equation*} So  $\psi_{\mathbf{K}_\bullet, A}^{M, I}(n) \geq \ell(I^{n-1}M/I^nM)$ for all
$\psi_{\mathbf{K}_\bullet, A}^{M, I}(n) \geq \ell(I^{n-1}M/I^nM)$ for all ![]() $n \geq n_0$. So
$n \geq n_0$. So ![]() $r \geq d -1$. Thus
$r \geq d -1$. Thus ![]() $r = d -1$. By Theorem 1.2, it follows that
$r = d -1$. By Theorem 1.2, it follows that ![]() $r_I^M = r = d -1$.
$r_I^M = r = d -1$.
5. Proof of Theorem 1.8
In this section, we give a proof of Theorem 1.8. We need the following well-known result. Suppose ![]() $\dim E \gt 0$. Then, there exists
$\dim E \gt 0$. Then, there exists ![]() $x \in \mathfrak{m} $ such that
$x \in \mathfrak{m} $ such that ![]() $(0 \colon_E x)$ has finite length and
$(0 \colon_E x)$ has finite length and ![]() $\dim E/xE = \dim E - 1$.
$\dim E/xE = \dim E - 1$.
We now give
Proof of Theorem 1.8
By 1.7, it suffices to consider the case when ![]() $\dim H^*(\mathbf{X}_\bullet \otimes M) \leq \dim M -1$.
$\dim H^*(\mathbf{X}_\bullet \otimes M) \leq \dim M -1$.
We first consider the case when ![]() $\dim H^*(\mathbf{X}_\bullet \otimes M) = 0$. We prove the result by inducting on
$\dim H^*(\mathbf{X}_\bullet \otimes M) = 0$. We prove the result by inducting on ![]() $\dim H^*(\mathbf{X}_\bullet)$. If
$\dim H^*(\mathbf{X}_\bullet)$. If ![]() $\dim H^*(\mathbf{X}_\bullet) = 0$ then the result follows from Theorem 1.4. If
$\dim H^*(\mathbf{X}_\bullet) = 0$ then the result follows from Theorem 1.4. If ![]() $\dim H^*(\mathbf{X}_\bullet) \gt 0$ then choose x such that map
$\dim H^*(\mathbf{X}_\bullet) \gt 0$ then choose x such that map ![]() $ H^*(\mathbf{X}_\bullet) \xrightarrow{x} H^*(\mathbf{X}_\bullet)$ has finite length kernel and
$ H^*(\mathbf{X}_\bullet) \xrightarrow{x} H^*(\mathbf{X}_\bullet)$ has finite length kernel and ![]() $\dim H^*(\mathbf{X}_\bullet)/xH^*(\mathbf{X}_\bullet) = \dim H^*(\mathbf{X}_\bullet) -1$. Consider the triangle
$\dim H^*(\mathbf{X}_\bullet)/xH^*(\mathbf{X}_\bullet) = \dim H^*(\mathbf{X}_\bullet) -1$. Consider the triangle ![]() $\mathbf{X}_\bullet \xrightarrow{x} \mathbf{X}_\bullet \rightarrow \mathbf{Y}_\bullet \rightarrow \mathbf{X}_\bullet[1]$. By taking long exact sequence of homology, we get an exact sequence
$\mathbf{X}_\bullet \xrightarrow{x} \mathbf{X}_\bullet \rightarrow \mathbf{Y}_\bullet \rightarrow \mathbf{X}_\bullet[1]$. By taking long exact sequence of homology, we get an exact sequence
It follows that ![]() $\dim H^*(\mathbf{Y}_\bullet) = \dim H^*(\mathbf{X}_\bullet) - 1$. Furthermore note
$\dim H^*(\mathbf{Y}_\bullet) = \dim H^*(\mathbf{X}_\bullet) - 1$. Furthermore note
![]() $\mathbf{Z}_\bullet = \operatorname{cone}(x, \mathbf{X}_\bullet) \cong \mathbf{Y}_\bullet$. We have an exact sequence
$\mathbf{Z}_\bullet = \operatorname{cone}(x, \mathbf{X}_\bullet) \cong \mathbf{Y}_\bullet$. We have an exact sequence
As ![]() $\mathbf{X}_\bullet^i$ is free for all i we have an exact sequence for all
$\mathbf{X}_\bullet^i$ is free for all i we have an exact sequence for all ![]() $n \geq 0$
$n \geq 0$
and
By considering later short exact sequence of complexes, we get by looking at long exact sequence in homology that ![]() $\dim H^*(\mathbf{Z}_\bullet\otimes M) = 0$. So by induction hypothesis
$\dim H^*(\mathbf{Z}_\bullet\otimes M) = 0$. So by induction hypothesis ![]() $s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. By considering all
$s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. By considering all ![]() $n \geq 1$ and summing all i, we get
$n \geq 1$ and summing all i, we get
 \begin{equation*}
\psi_{\mathbf{Y}_\bullet}^{M, I}(n) \leq 2 \psi_{\mathbf{X}_\bullet}^{M, I}(n).
\end{equation*}
\begin{equation*}
\psi_{\mathbf{Y}_\bullet}^{M, I}(n) \leq 2 \psi_{\mathbf{X}_\bullet}^{M, I}(n).
\end{equation*} It follows that ![]() $s_I^M(\mathbf{X}_\bullet) \geq s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. But
$s_I^M(\mathbf{X}_\bullet) \geq s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. But ![]() $s_I^M(\mathbf{X}_\bullet) \leq \dim M -1$. The result follows.
$s_I^M(\mathbf{X}_\bullet) \leq \dim M -1$. The result follows.
We now assume ![]() $ 0 \lt a = \dim H^*(\mathbf{X}_\bullet \otimes M) \leq \dim M -1$ and the result is proved for complexes
$ 0 \lt a = \dim H^*(\mathbf{X}_\bullet \otimes M) \leq \dim M -1$ and the result is proved for complexes ![]() $\mathbf{Z}_\bullet$ with
$\mathbf{Z}_\bullet$ with ![]() $\dim H^*(\mathbf{Z}_\bullet \otimes M) = a -1$. Choose x such that map
$\dim H^*(\mathbf{Z}_\bullet \otimes M) = a -1$. Choose x such that map ![]() $ H^*(\mathbf{X}_\bullet \otimes M) \xrightarrow{x} H^*(\mathbf{X}_\bullet\otimes M)$ has finite length kernel and
$ H^*(\mathbf{X}_\bullet \otimes M) \xrightarrow{x} H^*(\mathbf{X}_\bullet\otimes M)$ has finite length kernel and ![]() $\dim H^*(\mathbf{X}_\bullet \otimes M)/xH^*(\mathbf{X}_\bullet \otimes M) = \dim H^*(\mathbf{X}_\bullet \otimes M) -1$. Consider the triangle
$\dim H^*(\mathbf{X}_\bullet \otimes M)/xH^*(\mathbf{X}_\bullet \otimes M) = \dim H^*(\mathbf{X}_\bullet \otimes M) -1$. Consider the triangle ![]() $\mathbf{X}_\bullet \xrightarrow{x} \mathbf{X}_\bullet \rightarrow \mathbf{Y}_\bullet \rightarrow \mathbf{X}_\bullet[1]$. Note
$\mathbf{X}_\bullet \xrightarrow{x} \mathbf{X}_\bullet \rightarrow \mathbf{Y}_\bullet \rightarrow \mathbf{X}_\bullet[1]$. Note ![]() $\mathbf{Z}_\bullet = \operatorname{cone}(x, \mathbf{X}_\bullet) \cong \mathbf{Y}_\bullet$. We have an exact sequence
$\mathbf{Z}_\bullet = \operatorname{cone}(x, \mathbf{X}_\bullet) \cong \mathbf{Y}_\bullet$. We have an exact sequence
As ![]() $\mathbf{X}_\bullet^i$ is free for all i, we have an exact sequence for all
$\mathbf{X}_\bullet^i$ is free for all i, we have an exact sequence for all ![]() $n \geq 0$
$n \geq 0$
and
By considering the latter short exact sequence of complexes, we get by looking at long exact sequence in homology we get an exact sequence
Therefore ![]() $\dim H^*(\mathbf{Z}_\bullet\otimes M) = \dim H^*(\mathbf{X}_\bullet\otimes M) - 1$. So by induction hypothesis
$\dim H^*(\mathbf{Z}_\bullet\otimes M) = \dim H^*(\mathbf{X}_\bullet\otimes M) - 1$. So by induction hypothesis ![]() $s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. By considering all
$s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. By considering all ![]() $n \geq 1$ and summing all i, we get
$n \geq 1$ and summing all i, we get
 \begin{equation*}
\psi_{\mathbf{Y}_\bullet}^{M, I}(n) \leq 2 \psi_{\mathbf{X}_\bullet}^{M, I}(n)
\end{equation*}
\begin{equation*}
\psi_{\mathbf{Y}_\bullet}^{M, I}(n) \leq 2 \psi_{\mathbf{X}_\bullet}^{M, I}(n)
\end{equation*} It follows that ![]() $s_I^M(\mathbf{X}_\bullet) \geq s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. But
$s_I^M(\mathbf{X}_\bullet) \geq s_I^M(\mathbf{Y}_\bullet) = \dim M -1$. But ![]() $s_I^M(\mathbf{X}_\bullet) \leq \dim M -1$. The result follows.
$s_I^M(\mathbf{X}_\bullet) \leq \dim M -1$. The result follows.
6. Proof of Corollary 1.10
In this section, we give a proof of Corollary 1.10. We need the following result:
Lemma 6.1. Let A be a Cohen–Macaulay local ring and let L be a nonzero A-module of finite projective dimension. Then
Proof. It is clear that ![]() $\operatorname{Supp} (M\otimes L) = \operatorname{Supp} M \cap \operatorname{Supp} L$. Thus, it follows that
$\operatorname{Supp} (M\otimes L) = \operatorname{Supp} M \cap \operatorname{Supp} L$. Thus, it follows that ![]() $\operatorname{Supp} \operatorname{Ext}^*_A(L, M) \subseteq \operatorname{Supp} (M \otimes L)$. Conversely let
$\operatorname{Supp} \operatorname{Ext}^*_A(L, M) \subseteq \operatorname{Supp} (M \otimes L)$. Conversely let ![]() $P \in \operatorname{Supp} M \otimes L$. We localize at P. So it suffices to prove
$P \in \operatorname{Supp} M \otimes L$. We localize at P. So it suffices to prove ![]() $\operatorname{Ext}^*(L, M) \neq 0$. By taking a minimal resolution of L, it clear that if
$\operatorname{Ext}^*(L, M) \neq 0$. By taking a minimal resolution of L, it clear that if ![]() $c = \operatorname{projdim} L$ then
$c = \operatorname{projdim} L$ then ![]() $\operatorname{Ext}^c_A(L,M) \neq 0$. The result follows.
$\operatorname{Ext}^c_A(L,M) \neq 0$. The result follows.
We now give
Proof of Corollary 1.10
Let ![]() $\mathbf{X}_\bullet$ be a minimal projective resolution of L. Then
$\mathbf{X}_\bullet$ be a minimal projective resolution of L. Then
![]() $t^I_M(L, n) = \ell(H^*(\mathbf{X}_\bullet \otimes M/I^nM))$. By 1.8, it follows that
$t^I_M(L, n) = \ell(H^*(\mathbf{X}_\bullet \otimes M/I^nM))$. By 1.8, it follows that
The result follows as ![]() $\dim H^*(\mathbf{X}_\bullet \otimes M) = \dim M \otimes L$.
$\dim H^*(\mathbf{X}_\bullet \otimes M) = \dim M \otimes L$.
Set ![]() $\mathbf{X}_\bullet^* = \operatorname{Hom}_A(\mathbf{X}_\bullet, A)$. Observe
$\mathbf{X}_\bullet^* = \operatorname{Hom}_A(\mathbf{X}_\bullet, A)$. Observe
So
Notice ![]() $H^*(\mathbf{X}_\bullet^* \otimes M) = \operatorname{Ext}^*_A(L, M)$. The results follows from Lemma 6.1.
$H^*(\mathbf{X}_\bullet^* \otimes M) = \operatorname{Ext}^*_A(L, M)$. The results follows from Lemma 6.1.
Data availability statement
No data (public or private) were used in this paper.