Hostname: page-component-5cf477f64f-bmd9x Total loading time: 0 Render date: 2025-04-02T14:21:38.733Z Has data issue: false hasContentIssue false
  • English
  • Français

Decomposition of a Von Neumann Algebra Relative to a*-Automorphism

Published online by Cambridge University Press:  20 January 2009

A. B. Thaheem
A. B. Thaheem
Affiliation:
Quaid-I-Azam University, Islamabad, Pakistan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X be any real or complex Banach space. If T is a bounded linear operator on X then denote by N(T) the null space of T and by R(T) the range space of T.

Now if X is finite dimensional and N(T) = N(T2) then also R(T) = R(T2). Therefore X admits a direct sum decomposition

.

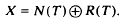Indeed it is easy to see that N(T) = N(T2) implies that 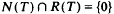and, using dimension theory of finite dimensional spaces, that N(T) and R(T) span the whole space (see, for example, (2, pp. 271–73))

Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 22 , Issue 1 , February 1979 , pp. 9 - 10
Copyright
Copyright © Edinburgh Mathematical Society 1979

References

REFERNCES

(1) Dixmier, J., Les Algèbres d'opérateurs dans I'Espace Hilbertien (Gauthier-Villars, Paris, 2nd ed. 1969).Google Scholar
(2) Taylor, A. E., Introduction to Functional Analysis (Wiley, John & Sons, , New York, Top con Co, Ltd. Tokyo, 1958).Google Scholar