Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-23T16:55:06.460Z Has data issue: false hasContentIssue false
  • English
  • Français

A criterion for normality of analytic mappings

Part of: Entire and meromorphic functions, and related topics Spaces and algebras of analytic functions Holomorphic functions of several complex variables

Published online by Cambridge University Press:  19 November 2021

Marijan Marković
Marijan Marković*
Affiliation:
Faculty of Sciences and Mathematics, University of Montenegro, Podgorica81 000, Montenegro ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we give a generalization and improvement of the Pavlović result on the characterization of continuously differentiable functions in the Bloch space on the unit ball in $\mathbb {R}^{m}$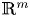. Then, we derive a Holland–Walsh type theorem for analytic normal mappings on the unit disk.

Keywords

normal analytic functionBloch analytic functionhyperbolic distancespherical distanceBloch type spacesLipschitz type spaces

MSC classification

Primary: 30D45: Bloch functions, normal functions, normal families
Secondary: 30H30: Bloch spaces 32A18: Bloch functions, normal functions
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 80 - 88
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anderson, J., Clunie, J. and Pommerenke, Ch., On Bloch functions and normal functions, J. die reine und angewandte Math. 270 (1974), 12–37.Google Scholar
Colonna, F., Bloch and normal functions and their relation, Rendiconti del Circolo Matematico di Palermo Series 2 38 (1989), 161–180.CrossRefGoogle Scholar
Colonna, F., The Bloch constant of bounded harmonic mappings, Indiana Univ. Math. J. 38 (1989), 829–840.CrossRefGoogle Scholar
Holland, F. and Walsh, D., Criteria for membership of Bloch space and its subspace, BMOA, Math. Ann. 273 (1986), 317–335.CrossRefGoogle Scholar
Marković, M., Differential-free characterisation of smooth mappings with given growth, Canad. Math. Bull. 61 (2018), 628–636.CrossRefGoogle Scholar
Pavlović, M., On the Holland–Walsh characterization of Bloch functions, Proc. Edinburgh Math. Soc. 51 (2008), 439–441.CrossRefGoogle Scholar
Ren, G. and Kähler, U., Weighted Lipschitz continuity and harmonic Bloch and Besov spaces, Proc. Edinb. Math. Soc. 48 (2005), 743–755.CrossRefGoogle Scholar
Ren, G. and Tu, C., Bloch space in the unit ball of $\mathbb {C}^{n}$, Proc. Am. Math. Soc. 133 (2005), 719–726.CrossRefGoogle Scholar
Zhu, K., Distances and Banach spaces of holomorphic functions on complex domains, J. London Math. Soc. 49 (1994), 163–182.CrossRefGoogle Scholar