Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-25T21:36:38.668Z Has data issue: false hasContentIssue false
  • English
  • Français

Some generating functions and inequalities for the andrews–stanley partition functions

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  27 December 2021

Na Chen ,
Shane Chern ,
Yan Fan  and
Ernest X. W. Xia
Na Chen
Affiliation:
School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou, Jiangsu215009, P. R. China ([email protected], [email protected])
Shane Chern
Affiliation:
Department of Mathematics and Statistics, Dalhousie University, Halifax, Nova ScotiaB3H 4R2, Canada ([email protected])
Yan Fan
Affiliation:
Department of Mathematics, Jiangsu University, Zhenjiang, Jiangsu212013, P. R. China ([email protected])
Ernest X. W. Xia
Affiliation:
School of Mathematical Sciences, Suzhou University of Science and Technology, Suzhou, Jiangsu215009, P. R. China ([email protected], [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $\mathcal {O}(\pi )$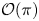 denote the number of odd parts in an integer partition $\pi$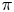. In 2005, Stanley introduced a new statistic $\operatorname {srank}(\pi )=\mathcal {O}(\pi )-\mathcal {O}(\pi ')$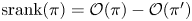, where $\pi '$ 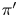is the conjugate of $\pi$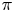. Let $p(r,\,m;n)$ 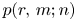denote the number of partitions of $n$ 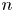with srank congruent to $r$ 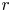modulo $m$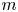. Generating function identities, congruences and inequalities for $p(0,\,4;n)$ 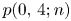and $p(2,\,4;n)$ 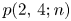were then established by a number of mathematicians, including Stanley, Andrews, Swisher, Berkovich and Garvan. Motivated by these works, we deduce some generating functions and inequalities for $p(r,\,m;n)$ 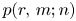with $m=16$ 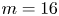and $24$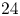. These results are refinements of some inequalities due to Swisher.

Keywords

Andrews–Stanley partition functionrankcrankpartition inequalityasymptotic formula

MSC classification

Primary: 11P81: Elementary theory of partitions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 120 - 135
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Abramowitz, M. and Stegun, I. A., eds. Handbook of mathematical functions with formulas, graphs, and mathematical tables (United States Department of Commerce, National Bureau of Standards, 10th printing, 1972).Google Scholar
Andrews, G. E., On a partition function of Richard Stanley, Electron. J. Combin. 11(2) (2004), 10. Research Paper 1.CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G., Dissecting the Stanley partition function, J. Combin. Theory Ser. A 112(2) (2005), 277–291.CrossRefGoogle Scholar
Berkovich, A. and Garvan, F. G., On the Andrews-Stanley refinement of Ramanujan's partition congruence modulo 5 and generalizations, Trans. Amer. Math. Soc. 358(2) (2006), 703–726.CrossRefGoogle Scholar
Berndt, B. C., Ramanujan's notebooks, Part III, (Springer, New York, 1991).CrossRefGoogle Scholar
Chern, S., Asymptotics for the Fourier coefficients of eta-quotients, J. Number Theory 199 (2019), 168–191.CrossRefGoogle Scholar
Hardy, G. H. and Ramanujan, S., Asymptotic formulae in combinatory analysis, Proc. London Math. Soc. (2) 17 (1918), 75–115.CrossRefGoogle Scholar
Rademacher, H., On the partition function $p(n)$, Proc. London Math. Soc. (2) 43(4) (1937), 241–254.Google Scholar
Stanley, R. P., Problem 10969, Amer. Math. Monthly 109(8) (2002), 760.CrossRefGoogle Scholar
Stanley, R. P., Some remarks on sign-balanced and maj-balanced posets, Adv. Appl. Math. 34(4) (2005), 880–902.CrossRefGoogle Scholar
Sussman, E., Rademacher series for $\eta$-quotients, preprint (2017). Available at arXiv:1710.03415.Google Scholar
Swisher, H., Asymptotics and congruence properties for Stanley's partition function, and a note on a theorem of Koike, Ph.D. Thesis, University of Wisconsin-Madison (2005).Google Scholar
Swisher, H., The Andrews–Stanley partition function and $p(n)$: congruences, Proc. Amer. Math. Soc. 139(4) (2011), 1175–1185.CrossRefGoogle Scholar