Hostname: page-component-745bb68f8f-s22k5 Total loading time: 0 Render date: 2025-02-03T09:13:57.375Z Has data issue: false hasContentIssue false
  • English
  • Français

Some embeddings between symmetric R. thompson groups

Part of: Structure and classification of infinite or finite groups Special aspects of infinite or finite groups

Published online by Cambridge University Press:  07 December 2021

Julio Aroca  and
Collin Bleak
Julio Aroca
Affiliation:
Instituto de Ciencias Matemáticas, Madrid, Spain ([email protected])
Collin Bleak
Affiliation:
University of St Andrews, St Andrews, UK ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

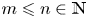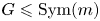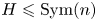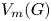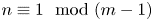Let $m\leqslant n\in \mathbb {N}$, and $G\leqslant \operatorname {Sym}(m)$ and $H\leqslant \operatorname {Sym}(n)$. In this article, we find conditions enabling embeddings between the symmetric R. Thompson groups ${V_m(G)}$ and ${V_n(H)}$. When $n\equiv 1 \mod (m-1)$, and under some other technical conditions, we find an embedding of ${V_n(H)}$ 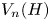into ${V_m(G)}$ 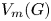via topological conjugation. With the same modular condition, we also generalize a purely algebraic construction of Birget from 2019 to find a group $H\leqslant \operatorname {Sym}(n)$ 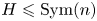and an embedding of ${V_m(G)}$ 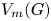into ${V_n(H)}$.

Keywords

R. Thompson groupsembeddingstopological conjugacyFSS Groups

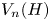MSC classification

Primary: 20E07: Subgroup theorems; subgroup growth
Secondary: 20E34: General structure theorems 20F65: Geometric group theory
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 1 - 18
Check for updates
Copyright
Copyright © The Author(s), 2021. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Birget, J. C., New embeddings between the Higman-Thompson groups, Commun. Algebra 48(8) (2020), 3429–3438.CrossRefGoogle Scholar
Bleak, C. and Lanoue, D., A family of non-isomorphism results, Geom. Dedicata 146 (2010), 21–26.CrossRefGoogle Scholar
Bleak, C., Donoven, C. and Jonušas, J., Some isomorphism results for Thompson-like groups $V_n(G)$, Israel J. Math. 222(1) (2017), 1–19.CrossRefGoogle Scholar
Bleak, C., Matucci, F. and Neunhöffer, M., Embeddings into Thompson's group $V$ and $co\mathcal {CF}$ groups, J. Lond. Math. Soc. (2) 94(2) (2016), 583–597.CrossRefGoogle Scholar
Bon, N. M., Rigidity properties of full groups of pseudogroups over the cantor set, available at https://arxiv.org/pdf/1801.10133.pdf (2018).Google Scholar
Brouwer, L. E. J., On the structure of perfect sets of points, in KNAW, Proceedings, Volume 12, pp. 1909–1910 (1910)Google Scholar
Farley, D., Local similarity groups with context-free co-word problem, in Topological methods in group theory, London Mathematical Society Lecture Note Series, Volume 451, pp. 67–91 (Cambridge University Press, Cambridge, 2018).Google Scholar
Grigorchuk, R. I., Nekrashevych, V. and Sushchanskiĭ, V., Automata, dynamical systems, and groups, Proc. Steklov Inst. Math 231(4) (2000), 128–203.Google Scholar
Higman, G., Finitely presented infinite simple groups. Department of Pure Mathematics, Department of Mathematics, I.A.S. Australian National University, Canberra, 1974. Notes on Pure Mathematics, No. 8 (1974)Google Scholar
Holt, D. F., Rees, S., Röver, C. E. and Thomas, R. M., Groups with context-free co-word problem, J. London Math. Soc. (2) 71(3) (2005), 643–657.CrossRefGoogle Scholar
Hughes, B., Local similarities and the Haagerup property, Groups Geom. Dyn. 3(2) (2009), 299–315, With an appendix by Daniel S. Farley.CrossRefGoogle Scholar
Lehnert, J., Gruppen von quasi-automorphismen. PhD thesis, Goethe Universität, Frankfurt, 2008.Google Scholar
Lehnert, J. and Schweitzer, P., The co-word problem for the Higman-Thompson group is context-free, Bull. Lond. Math. Soc. 39(2) (2007), 235–241.CrossRefGoogle Scholar
Nekrashevych, V. V., Cuntz-Pimsner algebras of group actions, J. Oper. Theory 52(2) (2004), 223–249.Google Scholar
Röver, C. E., Constructing finitely presented simple groups that contain Grigorchuk groups, J. Algebra 220(1) (1999), 284–313.CrossRefGoogle Scholar
Scott, E. A., A construction which can be used to produce finitely presented infinite simple groups, J. Algebra 90(2) (1984), 294–322.CrossRefGoogle Scholar
Scott, E. A., A finitely presented simple group with unsolvable conjugacy problem, J. Algebra 90(2) (1984), 333–353.CrossRefGoogle Scholar
Scott, E. A., The embedding of certain linear and abelian groups in finitely presented simple groups, J. Algebra 90(2) (1984), 323–332.CrossRefGoogle Scholar