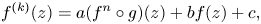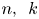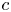Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
He, Zhongwei
and
Gao, Lingyun
2023.
Interval estimation on hyper-order of meromorphic solutions of complex linear differential equations with uncertain coefficients.
Applied Mathematics in Science and Engineering,
Vol. 31,
Issue. 1,