Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-23T16:36:49.840Z Has data issue: false hasContentIssue false
  • English
  • Français

On Commuting Varieties of Nilradicals of Borel Subalgebras of Reductive Lie Algebras

Part of: Linear algebraic groups and related topics Lie algebras and Lie superalgebras

Published online by Cambridge University Press:  10 October 2014

Simon M. Goodwin  and
Gerhard Röhrle
Simon M. Goodwin
Affiliation:
School of Mathematics, University of Birmingham, Birmingham B15 2TT, UK, ([email protected])
Gerhard Röhrle
Affiliation:
Fakultät für MathematikRuhr-Universität Bochum, D-44780 Bochum, Germany, ([email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G be a connected reductive algebraic group defined over an algebraically closed field 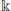of characteristic 0. We consider the commuting variety 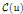of the nilradical 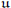of the Lie algebra 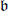of a Borel subgroup B of G. In case B acts on 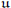with only a finite number of orbits, we verify that 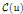is equidimensional and that the irreducible components are in correspondence with the distinguishedB-orbits in 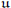. We observe that in general 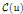is not equidimensional, and determine the irreducible components of 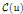in the minimal cases where there are infinitely many B-orbits in .

Keywords

commuting varietiesBorel subalgebrasLie algebrasalgebraic groups

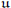MSC classification

Primary: 20G15: Linear algebraic groups over arbitrary fields
Secondary: 17B45: Lie algebras of linear algebraic groups
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 58 , Issue 1 , February 2015 , pp. 169 - 181
Copyright
Copyright © Edinburgh Mathematical Society 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bourbaki, N., Groupes et algèbres de Lie, Chapters 4-6 (Hermann, Paris, 1975).Google Scholar
2.Bürgstein, H. and Hesselink, W. H., Algorithmic orbit classification for some Borel group actions, Compositio Math. 61(1) (1987), 3–41.Google Scholar
3.Goodwin, S. M. and Röhrle, G., Calculating conjugacy classes in Sylow p-subgroups of finite Chevalley groups, J. Alg. 321(11) (2009), 3321–3334.CrossRefGoogle Scholar
4.Hille, L. and Röhrle, G., A classification of parabolic subgroups of classical groups with a finite number of orbits on the unipotent radical, Transform. Groups 4(1) (1998), 317–337.Google Scholar
5.Kashin, V. V., Orbits of an adjoint and co-adjoint action of Borel subgroups of a semisimple algebraic group, in Problems in group theory and homological algebra, pp. 141–158 (Yaroslavl State University, 1990).Google Scholar
6.Keeton, A. G., Commuting varieties associated with symmetric pairs, PhD thesis, University of California (1995).Google Scholar
7.Kraft, H., Geometrische Methoden in der Invariantentheorie, Aspects of Mathematics: D, Volume 1 (Vieweg, Braunschweig, 1984).CrossRefGoogle Scholar
8.Levy, P., Commuting varieties of Lie algebras over fields of prime characteristic, J. Alg. 250(2) (2002), 473–484.Google Scholar
9.Premet, A., Nilpotent commuting varieties of reductive Lie algebras, Invent. Math. 154(3) (2003), 653–683.Google Scholar
10.Richardson, R. W., Commuting varieties of semisimple Lie algebras and algebraic groups, Compositio Math. 38(3) (1979), 311–327.Google Scholar