Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-26T11:00:40.815Z Has data issue: false hasContentIssue false
  • English
  • Français

An asynchronous inertial algorithm for solving convex feasibility problems with strict pseudo-contractions in Hilbert spaces

Part of: Nonlinear operators and their properties Equations and inequalities involving nonlinear operators

Published online by Cambridge University Press:  18 February 2022

A.U. Bello Open the ORCID record for A.U. Bello [Opens in a new window]  and
M.O. Nnakwe
A.U. Bello
Affiliation:
African University of Science and Technology, Abuja, Nigeria ([email protected]; [email protected]) Federal University, Dutsin-Ma, Katsina State, Nigeria
M.O. Nnakwe
Affiliation:
African University of Science and Technology, Abuja, Nigeria ([email protected]; [email protected]) Department of Mathematics and Statistics, Auburn University, Alabama, AL36849, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

Finding a common point in a finite intersection of sets, say, $C=\cap _{i=1}^{n} F(T_i)$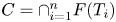, where each $T_i$ 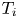is a non-expansive-type mapping, is a central task in mathematics as it cuts across different areas of application, such as road design and medical image reconstruction. There are many algorithms for approximating solutions of such problems. Of particular interest in the implementation of these algorithms are cost and speed. This is due to the large computations to be performed at each step of the iterative process. One of the most efficient methods that optimizes the time of computation and cost of implementation is the asynchronous-parallel algorithm method. In this paper, we prove a weak convergence theorem for the asynchronous sequential inertial (ASI) algorithm (introduced by Heaton and Censor in [H. Heaton and Y. Censor, Asynchronous sequential inertial iterations for common fixed points problems with an application to linear systems, J. Glob. Optim. 74 (2019), 95–119.] ) for strictly pseudo-contractive mappings in Hilbert spaces. Under additional mild conditions, we also obtain a strong convergence theorem. Finally, we apply the ASI algorithm to solving convex minimization problems and Hammerstein integral equations.

Keywords

convex feasibility problemsasynchronous-parallel algorithmsstrict pseudo-contractions

MSC classification

Primary: 47H04: Set-valued operators 47H06: Accretive operators, dissipative operators, etc. 47J25: Iterative procedures
Type
Research Article
Information
Proceedings of the Edinburgh Mathematical Society , Volume 65 , Issue 1 , February 2022 , pp. 229 - 243
Check for updates
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on Behalf of The Edinburgh Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aharoni, D. and Barak, A., Parallel iterative discontinuous Galerkin finite-element methods, in Discontinuous Galerkin methods, pp. 247–254 (Springer, 2000)CrossRefGoogle Scholar
Aharoni, R. and Censor, Y., Block-iterative projection methods for parallel computation of solutions to convex feasibility problems, Linear Algebra Appl. 120 (1989), 165–175.CrossRefGoogle Scholar
Amitai, D., Averbuch, A., Israeli, M. and Itzikowitz, S., Implicit-explicit parallel asynchronous solver of parabolic pdes, SIAM J. Sci. Comput. 19 (4) (1998), 1366–1404.CrossRefGoogle Scholar
Bahi, J., Miellou, J. C. and Rhofir, K., Asynchronous multisplitting methods for nonlinear fixed point problems, Numer. Algor. 15 (3–4) (1997), 315–345.CrossRefGoogle Scholar
Baillon, J. B. and Haddad, G., Quelques propriétés des oprateurs angle-bornés et n-cycliquement monotones, Israel J. Math. 26 (1977), 137–50.CrossRefGoogle Scholar
Baillon, J.-B., Bruck, R. E. and Reich, S., On the asymptotic behavior of nonexpansive mappings and semigroups, Houston J. Math. 4 (1978), 1–9.Google Scholar
Baudet, G. M., Asynchronous iterative methods for multiprocessors, J. ACM (JACM) 25 (2) (1978), 226–244.CrossRefGoogle Scholar
Bauschke, H. H. and Borwein, J. M., On projection algorithms for solving convex feasibility problems, SIAM Rev. 38 (1996), 367–426.CrossRefGoogle Scholar
Bauschke, H. H. and Combettes, P. L., Convex analysis and monotone operator theory in Hilbert spaces (Springer, New York, 2011).CrossRefGoogle Scholar
Bauschke, H. H. and Koch, V., Projection methods: Swiss army knives for solving feasibility and best approximation problems with halfspaces, Contemp. Math. 636 (2015), 1–40.CrossRefGoogle Scholar
Bauschke, H., Combettes, P. L. and Kruk, S., Extrapolation algorithm for affine-convex feasibility problems, Numer. Algor. 41 (2006), 239–274.CrossRefGoogle Scholar
Bertsekas, D. P. and Tsitsiklis, J. N., Parallel and distributed computation: numerical methods, volume 23. (Prentice Hall, Englewood Cliffs, NJ, 1989).Google Scholar
Browder, F. E. and Petryshyn, W. V., Construction of fixed points of nonlinear mappings in Hilbert spaces, J. Math. Anal. Appl. 20 (1967), 197–228.CrossRefGoogle Scholar
Cegielski, A., Iterative methods for fixed point problems in Hilbert spaces (Springer, Heidelberg, 2012).Google Scholar
Cegielski, A., Reich, S. and Zalas, R., Weak, strong and linear convergence of the $CQ$-method via the regularity of Landweber operators, Optimization 69 (2020), 605–636.CrossRefGoogle Scholar
Censor, Y., Parallel application of block-iterative methods in medical imaging and radiation therapy, Math. Program. 42 (1988), 307–325.CrossRefGoogle Scholar
Censor, Y. and Cegielski, A., Projection methods: an annotated bibliography of books and reviews, Optimization 64 (2015), 2343–2358.CrossRefGoogle Scholar
Censor, Y. and Zenios, S. A., Parallel optimization, (Oxford University Press, New York, 1997).Google Scholar
Censor, Y., Gordon, M. and Gordon, R., Component averaging: an efficient iterative parallel algorithm for large and sparse unstructured problems, Parallel Comput. 27 (2001), 777–808.CrossRefGoogle Scholar
Censor, Y., Elfving, T., Kopf, N. and Bortfeld, T., The multiple-sets split feasibility problem and its applications for inverse problems, Inverse Probl. 21 (2005), 2071–2084.CrossRefGoogle Scholar
Censor, Y., Chen, W., Combettes, P. L., Davidi, R. and Herman, G. T., On the effectiveness of projection methods for convex feasibility problems with linear inequality constraints, Comput. Optim. Appl. 51 (2012), 1065–1088.CrossRefGoogle Scholar
Chau, M., Spiteri, P., Guivarch, R. and Boisson, H., Parallel asynchronous iterations for the solution of a 3d continuous flow electrophoresis problem, Comput. Fluids 37 (9) (2008), 1126–137.CrossRefGoogle Scholar
Chazan, D. and Miranker, W., Chaotic relaxation, Linear Algebra Appl. 2 (2) (1969), 199–222.CrossRefGoogle Scholar
Combettes, P. L., The convex feasibility problem in image recovery, Adv. Imaging Electron Phys. 95 (1996), 155–270.CrossRefGoogle Scholar
Combettes, P. L., Hilbertian convex feasibility problems: convergence of projection methods, Appl. Math. Optim. 35 (1997), 311–330.CrossRefGoogle Scholar
Combettes, P. L. and Eckstein, J., Asynchronous block-iterative primal-dual decomposition methods for monotone inclusions, Math. Program. 168 (2018), 645–672. doi: 10.1007/s10107-016-1044-0CrossRefGoogle Scholar
Donzis, D. A. and Aditya, K., Asynchronous finite-difference schemes for partial differential equations, J. Computat. Phys. 274 (2014), 370–392.CrossRefGoogle Scholar
Elsner, L., Koltracht, I. and Neumann, M., Convergence of sequential and asynchronous nonlinear paracontractions, Numer. Math. 62 (1992), 305–319.CrossRefGoogle Scholar
Geer, D., Chip makers turn to multicore processors, Computer 38 (2005), 11–13.CrossRefGoogle Scholar
Halpern, B., Fixed points of nonexpanding maps, Bull. Amer. Math. Soc. 73 (1967), 957–961.CrossRefGoogle Scholar
Heaton, H. and Censor, Y., Asynchronous sequential inertial iterations for common fixed points problems with an application to linear systems, J. Glob. Optim. 74 (2019), 95–119.CrossRefGoogle Scholar
Herman, G. T., Fundamentals of computerized tomography, (Springer, Dordrecht, 2009).CrossRefGoogle Scholar
Kim, T. H. and Xu, H. K., Strong convergence of modified Mann iterations, Nonlinear Anal. 61 (2005), 51–60.CrossRefGoogle Scholar
Lions, P. L., Approximation de points fixes de contractions, C. R. Acad. Sci. Sér. A-B Paris 284 (1977), 1357–1359.Google Scholar
Liu, J. and Wright, S. J., Asynchronous stochastic coordinate descent: parallelism and convergence properties, SIAM J. Optim. 25 (1) (2015), 351–376.CrossRefGoogle Scholar
Liu, J., Wright, S. J., Ré, C., Bittorf, V. and Sridhar, S., An asynchronous parallel stochastic coordinate descent algorithm, J. Mach. Learn. Res. 16 (2015), 285–322.Google Scholar
Mann, W. R., Mean value methods in iteration, Proc. Am. Math. Soc. 4 (1953), 506–510.CrossRefGoogle Scholar
Marino, G. and Xu, H. K., Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces, J. Math. Anal. Appl. 329 (2007), 336–346.CrossRefGoogle Scholar
Marino, G., Bruno, S. and Erdal, K., Strong convergence theorem for strict pseudo-contractions in Hilbert spaces, J. Inequal. Appl. 2016 (2016), 134.CrossRefGoogle Scholar
Masad, E. and Reich, S., A note on the multiple-set split convex feasibility problem in Hilbert space, J. Nonlinear Convex Anal. 8 (2007), 367–371.Google Scholar
Petryshyn, W., Construction of fixed points of demicompact mappings in Hilbert space, J. Math. Anal. Appl. 14 (2) (1966), 276–284.CrossRefGoogle Scholar
Reich, S., A limit theorem for projections, Linear Multilinear Algebra 9 (1983), 281–290.CrossRefGoogle Scholar
Reich, S., Weak convergence theorems for nonexpansive mappings in Banach spaces, J. Math. Anal. Appl. 67 (1979), 274–276.CrossRefGoogle Scholar
Tai, X. C. and Tseng, P., Convergence rate analysis of an asynchronous space decomposition method for convex minimization, Math. Comput. 71 (239) (2002), 1105–1135.CrossRefGoogle Scholar
Tseng, P., Bertsekas, D. and Tsitsiklis, J. N., Partially asynchronous, parallel algorithms for network flow and other problems, SIAM J. Control Optim. 28 (3) (1990), 678–710.CrossRefGoogle Scholar
Zhang, R. and Kwok, J., Asynchronous distributed ADMM for consensus optimization, in Proceedings of the 31st International Conference on Machine Learning (ICML-14), pp. 1701–1709 (2014).Google Scholar
Zhimin, P., Yangyang, X., Ming, Y. and Wotao, Y., An algorithmic framework for asynchronous parallel iterative coordinate updates, SIAM J. Sci. Comput. 38 (5) (2015), 024950.Google Scholar