Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T06:04:38.075Z Has data issue: false hasContentIssue false
  • English
  • Français

APPROXIMATION OF THE TAIL PROBABILITIES FOR BIDIMENSIONAL RANDOMLY WEIGHTED SUMS WITH DEPENDENT COMPONENTS

Published online by Cambridge University Press:  05 December 2018

Xinmei Shen ,
Mingyue Ge  and
Ke-Ang Fu
Xinmei Shen
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China E-mail: [email protected]; [email protected]
Mingyue Ge
Affiliation:
School of Mathematical Sciences, Dalian University of Technology, Dalian 116024, China E-mail: [email protected]; [email protected]
Ke-Ang Fu
Affiliation:
School of Statistics and Mathematics, Zhejiang Gongshang University, Hangzhou 310018, China E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 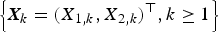$\left\{ {{\bi X}_k = {(X_{1,k},X_{2,k})}^{\top}, k \ge 1} \right\}$ be a sequence of independent and identically distributed random vectors whose components are allowed to be generally dependent with marginal distributions being from the class of extended regular variation, and let 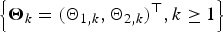$\left\{ {{\brTheta} _k = {(\Theta _{1,k},\Theta _{2,k})}^{\top}, k \ge 1} \right\}$ be a sequence of nonnegative random vectors that is independent of 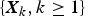$\left\{ {{\bi X}_k, k \ge 1} \right\}$. Under several mild assumptions, some simple asymptotic formulae of the tail probabilities for the bidimensional randomly weighted sums 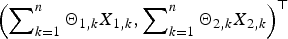$\left( {\sum\nolimits_{k = 1}^n {\Theta _{1,k}} X_{1,k},\sum\nolimits_{k = 1}^n {\Theta _{2,k}} X_{2,k}} \right)^{\rm \top }$ and their maxima 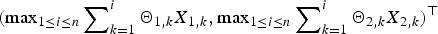$({{\max} _{1 \le i \le n}}\sum\nolimits_{k = 1}^i {\Theta _{1,k}} X_{1,k},{{\max} _{1 \le i \le n}}\sum\nolimits_{k = 1}^i {\Theta _{2,k}} X_{2,k})^{\rm \top }$ are established. Moreover, uniformity of the estimate can be achieved under some technical moment conditions on 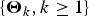$\left\{ {{\brTheta} _k, k \ge 1} \right\}$. Direct applications of the results to risk analysis are proposed, with two types of ruin probability for a discrete-time bidimensional risk model being evaluated.

Keywords

asymptoticsbidimensional randomly weighted sumscopulaextended regular variation
Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 34 , Issue 1 , January 2020 , pp. 112 - 130
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bingham, N.H., Goldie, C.M. & Teugels, J.L. (1987). Regular Variation Cambridge: Cambridge University Press.Google Scholar
2.Chen, Y.Q., Ng, K.W. & Xie, X.S. (2006). On the maximum of randomly weighted sums with regularly varying tails. Statistics and Probability Letters 76: 971–975.Google Scholar
3.Chen, Y.Q., Yuen, K.C. & Ng, K.W. (2011). Asymptotics for the ruin probabilities of a two-dimensional renewal risk model with heavy-tailed claims. Applied Stochastic Models in Business and Industry 27: 290–300.Google Scholar
4.Chen, Y., Wang, Y. & Wang, K. (2013). Asymptotic results for ruin probability of a two-dimensional renewal risk model. Stochastic Analysis and Applications 31(1): 80–91.Google Scholar
5.Cline, D.B.H. & Samorodnitsky, G. (1994). Subexponentiality of the product of independent random variables. Stochastic Processes and their Applications 49(1): 75–98.Google Scholar
6.Gao, Q. & Wang, Y. (2010). Randomly weighted sums with dominated varying-tailed increments and application to risk theory. The Journal of the Korean Statistical Society 39: 305–314.Google Scholar
7.Hazra, R.S. & Maulik, K. (2012). Tail behavior of randomly weighted sums. Advances in Applied Probability 44: 794–814.Google Scholar
8.Hu, Z. & Jiang, B. (2013). On joint ruin probabilities of a two-dimensional risk model with constant interest rate. Journal of Applied Probability 50(2): 309–322.Google Scholar
9.Huang, W., Weng, C.G. & Zhang, Y. (2014). Multivariate risk models under heavy-tailed risks. Applied Stochastic Models in Business and Industry 30: 341–360.Google Scholar
10.Li, J. (2016). Uniform asymptotics for a multi-dimensional time-dependent risk model with multivariate regularly varying claims and stochastic return. Insurance: Mathematics and Economics 71: 195–204.Google Scholar
11.Li, J. (2017). The infinite-time ruin probability for a bidimensional renewal risk model with constant force of interest and dependent claims. Communications in Statistics - Theory and Methods 46: 1959–1971.Google Scholar
12.Li, J. (2018). On the joint tail behavior of randomly weighted sums of heavy-tailed random variables. Journal of Multivariate Analysis 164: 40–53.Google Scholar
13.Li, J., Liu, Z. & Tang, Q. (2007). On the ruin probabilities of a bidimensional perturbed risk model. Insurance: Mathematics and Economics 41: 185–195.Google Scholar
14.Olvera-Cravioto, M. (2012). Asymptotics for weighted random sums. Advances in Applied Probability 44: 1142–1172.Google Scholar
15.Shen, X.M. & Zhang, Y. (2013). Ruin probabilities of a two-dimensional risk model with dependent risks of heavy tail. Statistics and Probability Letters 83: 1787–1799.Google Scholar
16.Shen, X.M., Lin, Z.Y. & Zhang, Y. (2009). Uniform estimate for maximum of randomly weighted sums with applications to ruin theory. Methodology and Computing in Applied Probability 11: 669–685.Google Scholar
17.Tang, Q. & Tsitsiashvili, G. (2003). Randomly weighted sums of subexponential random variables with application to ruin theory. Extremes 6: 171–188.Google Scholar
18.Tang, Q. & Tsitsiashvili, G. (2004). Finite and infinite time ruin probabilities in the presence of stochastic returns on investments. Advances in Applied Probability 36(4): 1278–1299.Google Scholar
19.Tang, Q. & Yuan, Z. (2014). Randomly weighted sums of subexponential random variables with application to capital allocation. Extremes 17: 467–493.Google Scholar
20.Yang, H. & Li, J. (2014). Asymptotic finite-time ruin probability for a bidimensional renewal risk model with constant interest force and dependent subexponential claims. Insurance: Mathematics and Economics 58: 185–192.Google Scholar
21.Zhang, Y. & Wang, W. (2012). Ruin probabilities of a bidimensional risk model with investment. Statistics and Probability Letters 82(1): 130–138.Google Scholar
22.Zhang, Y., Shen, X.M. & Weng, C.G. (2009). Approximation of the tail probability of randomly weighted sums and applications. Stochastic Processes and their Applications 119: 655–675.Google Scholar
23.Zhou, M., Wang, K. & Wang, Y. (2012). Estimates for the finite time ruin probability with insurance and financial risks. Acta Mathematicae Applicatae Sinica (English Series) 28: 795–806.Google Scholar