Hostname: page-component-586b7cd67f-r5fsc Total loading time: 0 Render date: 2024-11-23T13:51:35.597Z Has data issue: false hasContentIssue false
  • English
  • Français

TRAFFIC GENERATED BY A SEMI-MARKOV ADDITIVE PROCESS

Published online by Cambridge University Press:  02 November 2010

Joke Blom  and
Michel Mandjes
Joke Blom
Affiliation:
CWI 1098 XG Amsterdam, The Netherlands E-mail: [email protected]
Michel Mandjes
Affiliation:
Korteweg-de Vries Institute for Mathematics, University of Amsterdam, 1098 XH Amsterdam, The Netherlands; Eurandom, Eindhoven, The Netherlands; CWI, Amsterdam, The Netherlands E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a semi-Markov additive process A(·)—that is, a Markov additive process for which the sojourn times in the various states have general (rather than exponential) distributions. Letting the Lévy processes Xi(·), which describe the evolution of A(·) while the background process is in state i, be increasing, it is shown how double transforms of the type 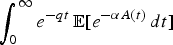can be computed. It turns out that these follow, for given nonnegative α and q, from a system of linear equations, which has a unique positive solution. Several extensions are considered as well.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 25 , Issue 1 , January 2011 , pp. 21 - 27
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Abate, J. & Whitt, W. (1995). Numerical inversion of Laplace transforms of probability distributions. ORSA Journal of Computations 7: 36–43.CrossRefGoogle Scholar
2.Anick, D., Mitra, D., & Sondhi, M. (1982). Stochastic theory of a data-handling system with multiple sources. Bell System Technical Journal 61: 1871–1894.CrossRefGoogle Scholar
3.Asmussen, S. (2003). Applied probability and queues, 2nd ed.Berlin: Springer.Google Scholar
4.Asmussen, S., Avram, F., & Pistorius, M. (2004). Russian and American put options under exponential phase-type Lévy models. Stochastic Processes and Their Applications 109: 79–111.CrossRefGoogle Scholar
5.Bertoin, J. (1996). Lévy processes. Cambridge: Cambridge University Press.Google Scholar
6.Boxma, O., Kella, O., & Perry, D. (2001). An intermittent fluid system with exponential on times and semi-Markov input rates. Probability in the Engineering and Informational Sciences 15: 189–198.CrossRefGoogle Scholar
7.Cohen, J.W. (1974). Superimposed renewal processes and storage with gradual input. Stochastic Processes and Their Applications 2: 31–58.CrossRefGoogle Scholar
8.den Iseger, P. (2006). Numerical transform inversion using Gaussian quadrature. Probability in the Engineering and Informational Sciences 20: 1–44.CrossRefGoogle Scholar
9.Dobrzyński, M. & Bruggeman, F. (2009). Elongation dynamics shape bursty transcription and translation. Proceedings of the National Academy of Sciences USA 106: 2583–2588.Google Scholar
10.Jobert, A. & Rogers, L. (2006). Option pricing with Markov-modulated dynamics. SIAM Journal on Control and Optimization 44: 2063–2078.CrossRefGoogle Scholar
11.Kesidis, G., Walrand, J., & Chang, C.-S. (1993). Effective bandwidths for multiclass Markov fluids and other ATM sources. IEEE/ACM Transactions on Networking 1: 424–428.CrossRefGoogle Scholar
12.Kosten, L. (1984). Stochastic theory of data-handling systems with groups of multiple sources. In: Rudin, H. & Bux, W. (eds.), Performance of computer-communication systems. Amsterdam: Elsevier, pp. 321–331.Google Scholar
13.Prabhu, N.U. (1998). Stochastic storage processes: Queues, insurance risk, dams, and data communication. New York: Springer-Verlag.CrossRefGoogle Scholar