Research Article
OPTIMAL BERNOULLI ROUTING IN AN UNRELIABLE M/G/1 RETRIAL QUEUE
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 1-20
-
- Article
- Export citation
TRAFFIC GENERATED BY A SEMI-MARKOV ADDITIVE PROCESS
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 21-27
-
- Article
- Export citation
UTILITY MAXIMIZATION IN A PURE JUMP MODEL WITH PARTIAL OBSERVATION
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 29-54
-
- Article
- Export citation
ON SKEWNESS AND DISPERSION AMONG CONVOLUTIONS OF INDEPENDENT GAMMA RANDOM VARIABLES
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 55-69
-
- Article
- Export citation
SOME NEW RESULTS ON ORDERING OF SIMPLE SPACINGS OF GENERALIZED ORDER STATISTICS
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 71-81
-
- Article
- Export citation
SOME NEW RELIABILITY BOUNDS FOR SUMS OF NBUE RANDOM VARIABLES
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 83-102
-
- Article
- Export citation
ROLLER-COASTER FAILURE RATES AND MEAN RESIDUAL LIFE FUNCTIONS WITH APPLICATION TO THE EXTENDED GENERALIZED INVERSE GAUSSIAN MODEL
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 103-118
-
- Article
- Export citation
TWO-PERSON RED-AND-BLACK GAME WITH LOWER LIMIT
-
- Published online by Cambridge University Press:
- 02 November 2010, pp. 119-133
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
PES volume 25 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 07 December 2010, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
PES volume 25 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 07 December 2010, pp. b1-b2
-
- Article
-
- You have access
- Export citation


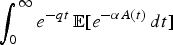 can be computed. It turns out that these follow, for given nonnegative α and
can be computed. It turns out that these follow, for given nonnegative α and 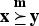 ) if
) if 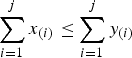 for
for 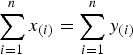 . A vector
. A vector 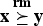 ) if
) if 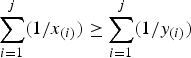 for
for 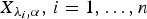 , be
, be 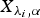 is a gamma random variable with shape parameter α≥1 and scale parameter λ
is a gamma random variable with shape parameter α≥1 and scale parameter λ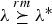 , then
, then 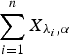 is greater than
is greater than 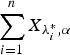 according to right spread order as well as mean residual life order. We also prove that if
according to right spread order as well as mean residual life order. We also prove that if 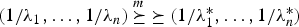 , then
, then 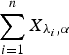 is greater than
is greater than 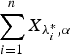 according to new better than used in expectation order as well as Lorenze order. These results mainly generalize the recent results of Kochar and Xu [7] and Zhao and Balakrishnan [14] from convolutions of independent exponential random variables to convolutions of independent gamma random variables with common shape parameters greater than or equal to 1.
according to new better than used in expectation order as well as Lorenze order. These results mainly generalize the recent results of Kochar and Xu [7] and Zhao and Balakrishnan [14] from convolutions of independent exponential random variables to convolutions of independent gamma random variables with common shape parameters greater than or equal to 1.