Hostname: page-component-586b7cd67f-2brh9 Total loading time: 0 Render date: 2024-11-25T08:11:31.177Z Has data issue: false hasContentIssue false
  • English
  • Français

DES AND RES PROCESSES AND THEIR EXPLICIT SOLUTIONS

Published online by Cambridge University Press:  22 December 2014

Michael N. Katehakis ,
Laurens C. Smit  and
Floske M. Spieksma
Michael N. Katehakis
Affiliation:
Department of Management Science and Information Systems, Rutgers Business School, Newark and New Brunswick, 100 Rockafeller Road, Piscataway, NJ 08854, USA E-mail: [email protected]
Laurens C. Smit
Affiliation:
Department of Management Science and Information Systems, Rutgers Business School, Newark and New Brunswick, 100 Rockafeller Road, Piscataway, NJ 08854, USA and Mathematisch Instituut, Universiteit Leiden, Niels Bohrweg 1, 2333 CA, The Netherlands E-mail: [email protected]
Floske M. Spieksma
Affiliation:
Mathematisch Instituut, Universiteit Leiden, Niels Bohrweg 1, 2333 CA, The Netherlands E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper defines and studies the down entrance state (DES) and the restart entrance state (RES) classes of quasi-skip free (QSF) processes specified in terms of the nonzero structure of the elements of their transition rate matrix Q. A QSF process is a Markov chain with states that can be specified by tuples of the form (m, i), where 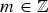$m \in {\open Z}$ represents the “current” level of the state and 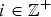$i \in {\open Z}^{+}$ the current phase of the state, and its transition probability matrix Q does not permit one-step transitions to states that are two or more levels away from the current state in one direction of the level variable m. A QSF process is a DES process if and only if one step “down” transitions from a level m can only reach a single state in level m − 1, for all m. A QSF process is a RES process if and only if one step “up” transitions from a level m can only reach a single set of states in the highest level M2, largest of all m.

We derive explicit solutions and simple truncation bounds for the steady-state probabilities of both DES and RES processes, when in addition Q insures ergodicity. DES and RES processes have applications in many areas of applied probability comprising computer science, queueing theory, inventory theory, reliability, and the theory of branching processes. To motivate their applicability we present explicit solutions for the well-known open problem of the M/Er/n queue with batch arrivals, an inventory model, and a reliability model.

Type
Research Article
Information
Probability in the Engineering and Informational Sciences , Volume 29 , Issue 2 , April 2015 , pp. 191 - 217
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Adan, I.J.B.F., Kapodistria, S. & van Leeuwaarden, J.S.H. (2013). Erlang arrivals joining the shorter queue. Queueing Systems, 74(2–3): 273–302.CrossRefGoogle Scholar
2.Artalejo, J.R., Economou, A. & Lopez-Herrero, M.J. (2010). The maximum number of infected individuals in SIS epidemic models: computational techniques and quasi-stationary distributions. Journal of computational and applied mathematics, 233(10): 2563–2574.CrossRefGoogle Scholar
3.Artalejo, J.R. & Gómez-Corral, A. (2008). Retrial queueing systems: a computational approach. Heidelberg: Springer–Verlag.CrossRefGoogle Scholar
4.Baer, N., Boucherie, R.J. & van Ommeren, J.C.W. (2013). The PH/PH/1 multi-threshold queue. Department of Applied Mathematics, University of Twente, Enschede, The Netherlands.Google Scholar
5.Bini, D., Latouche, G. & Meini, B. (2005). Numerical methods for structured Markov chains. Oxford University Press.CrossRefGoogle Scholar
6.Bini, D. & Meini, B. (1996). On the solution of a nonlinear matrix equation arising in queueing problems. SIAM Journal on Matrix Analysis and Applications, 17(4): 906–926.CrossRefGoogle Scholar
7.Bright, L. & Taylor, P.G. (1995). Calculating the equilibrium distribution in level dependent quasi-birth-and-death processes. Stochastic Models, 11(3): 497–525.CrossRefGoogle Scholar
8.Brown, M., Peköz, E.A. & Ross, S.M. (2010). Some results for skip-free random walk. Probability in the Engineering and Informational Sciences, 24(04): 491–507.CrossRefGoogle Scholar
9.Derman, C., Lieberman, G.J. & Ross, S.M. (1980). On the optimal assignment of servers and a repairman. Journal of Applied Probability, 17(2): 577–581.CrossRefGoogle Scholar
10.Etessami, K., Wojtczak, D. & Yannakakis, M. (2010). Quasi-birth-death processes, tree-like QBDs, probabilistic 1-counter automata, and pushdown systems. Performance Evaluation, 67(9): 837–857.CrossRefGoogle Scholar
11.Frostig, E. (1999). Jointly optimal allocation of a repairman and optimal control of service rate for machine repairman problem. European Journal of Operational Research, 116(2): 274–280,CrossRefGoogle Scholar
12.Gaver, D.P., Jacobs, P.A., Samorodnitsky, G. & Glazebrook, K.D. (2006). Modeling and analysis of uncertain time-critical tasking problems. Naval Research Logistics, 53(6): 588–599.CrossRefGoogle Scholar
13.Guillemin, F., Robert, P. & Zwart, A.P. (2004). AIMD algorithms and exponential functionals. The Annals of Applied Probability, 14(1): 90–117.CrossRefGoogle Scholar
14.Hooghiemstra, G. & Koole, G. (2000). On the convergence of the power series algorithm. Performance Evaluation, 42(1): 21–39.CrossRefGoogle Scholar
15.Hordijk, A. & Spieksma, F. (1992). On ergodicity and recurrence properties of a Markov chain with an application to an open Jackson network. Advances in Applied Probability, 24(2): 343–376.CrossRefGoogle Scholar
16.van Houdt, B. & van Leeuwaarden, J.S.H. (2011). Triangular M/G/1-type and tree-like quasi-birth-death Markov chains. INFORMS Journal on Computing, 23(1): 165–171.CrossRefGoogle Scholar
17.Kapodistria, S. (2011). The M/M/1 queue with synchronized abandonments. Queueing Systems, 68(1): 79–109.CrossRefGoogle Scholar
18.Katehakis, M.N. (1985). A note on the hypercube model. Operations Research Letters, 3(6): 319–322.CrossRefGoogle Scholar
19.Katehakis, M.N. & Derman, C. (1984). Optimal repair allocation in a series system. Mathematics of Operations Research, 9(4): 615–623.CrossRefGoogle Scholar
20.Katehakis, M.N. & Melolidakis, C. (1995). On the optimal maintenance of systems and control of arrivals in queues. Stochastic Analysis and Applications, 13(2): 137–164.CrossRefGoogle Scholar
21.Katehakis, M.N. & Smit, L.C. (2012). A successive lumping procedure for a class of Markov chains. Probability in the Engineering and Informational Sciences, 26(4): 483–508.CrossRefGoogle Scholar
22.Katehakis, M.N. & Veinott, A.F. Jr. (1987). The multi-armed bandit problem: decomposition and computation. Mathematics of Operations Research, 12(2): 262–268.CrossRefGoogle Scholar
23.Koole, G.M. & Spieksma, F.M. (2001). On deviation matrices for birth–death processes. Probability in the Engineering and Informational Sciences, 15(2): 239–258.CrossRefGoogle Scholar
24.Larson, R.C. (1974). A hypercube queuing model for facility location and redistricting in urban emergency services. Computers and Operations Research, 1(1): 67–95.CrossRefGoogle Scholar
25.Latouche, G. & Ramaswami, V. (1993). A logarithmic reduction algorithm for quasi-birth-death processes. Journal of Applied Probability, 650–674.CrossRefGoogle Scholar
26.Latouche, G. & Ramaswami, V. (1999). Introduction to matrix analytic methods in stochastic modeling., ASA–SIAM Series on Statistics and Applied Probability. Vol. 5, Philadelphia, PA: SIAM.CrossRefGoogle Scholar
27.Lin, K., Kress, M. & Szechtman, R. (2009). Scheduling policies for an antiterrorist surveillance system. Naval Research Logistics, 56(2): 113–126.CrossRefGoogle Scholar
28.Nash, P. & Weber, R.R. (1982). Dominant strategies in stochastic allocation and scheduling problems. In Deterministic and stochastic, scheduling. Dempster, M.H.A. et al. , eds. New York: Reidel Publishing Company, pp. 343–353.CrossRefGoogle Scholar
29.Neuts, M.F. (1981). Matrix-geometric solutions in Stochastic models – an algorithmic approach. New York: Dover Publications.Google Scholar
30.Pérez, J.F. & van Houdt, B. (2011). Quasi-birth-and-death processes with restricted transitions and its applications. Performance Evaluation, 68(2): 126–141.CrossRefGoogle Scholar
31.Ramaswami, V. (1988). A stable recursion for the steady state vector in Markov chains of M/G/1 type. Communications in Statistics. Stochastic Models, 4: 183–188.CrossRefGoogle Scholar
32.Righter, R. (1996). Optimal policies for scheduling repairs and allocating heterogeneous servers. Journal of Applied Probability, 436–547.Google Scholar
33.Riska, A. & Smirni, E. (2002). M/G/1-type Markov processes: a tutorial. Performance Evaluation of Complex Systems: Techniques and Tools, 2459: 36–63.CrossRefGoogle Scholar
34.Ross, S.M. (1996). Stochastic processes, Vol. 2. New York: Wiley.Google Scholar
35.Seneta, E. (1980). Computing the stationary distribution for infinite Markov chains. Linear Algebra and Its Applications, 34: 259–267.CrossRefGoogle Scholar
36.Seneta, E. (1981). Non-negative matrices and Markov chains. New York: Springer.CrossRefGoogle Scholar
37.Sonin, I.M. (2011). Optimal stopping of Markov chains and three abstract optimization problems. International Journal of Probability and Stochastic Processes, 83(4–6): 405–414.CrossRefGoogle Scholar
38.Spieksma, F.M. & Tweedie, R.L. (1994). Strengthening ergodicity to geometric ergodicity for Markov chains. Stochastic Models, 10(1): 45–74.CrossRefGoogle Scholar
39.Szpankowski, W. (1988). Stability conditions for multidimensional queueing systems with computer applications. Operations Research, 36(6): 944–957.CrossRefGoogle Scholar
40.Tong, H., Faloutsos, C. & Pan, J.Y. (2006). Fast random walk with restart and its applications. Data mining, ICDM ’06: Sixth International Conference on Data Mining, pp. 613–622.CrossRefGoogle Scholar
41.Tweedie, R.L. (1973). The calculation of limit probabilities for denumerable Markov processes from infinitesimal properties. Journal of Applied Probability, 84–99.CrossRefGoogle Scholar
42.Tweedie, R.L. (1981). Criteria for ergodicity, exponential ergodicity and strong ergodicity of Markov processes. Journal for Applied Probability, 18(1): 122–130.CrossRefGoogle Scholar
43.Ungureanu, V., Melamed, B. & Katehakis, M.N. (2008). Effective load balancing for cluster-based servers employing job preemption. Journal of Performance Evaluation, 65(8): 606–622.CrossRefGoogle Scholar
44.Ungureanu, V., Melamed, B., Katehakis, M.N. & Bradford, P.G. (2006). Deferred assignment scheduling in cluster-based servers. Cluster Computing, 9(2): 57–65.CrossRefGoogle Scholar
45.Varga, R.S. (1963). Matrix iterative analysis. Englewood Cliffs, NJ: Prentice-Hall.Google Scholar
46.Varga, R.S. (1976). On recurring theorems on diagonal dominance. Linear Algebra and its Applications, 13(1): 1–9.CrossRefGoogle Scholar
47.Veinott, A.F. Jr. (1965). The optimal inventory policy for batch ordering. Operations Research, 13: 424–432.CrossRefGoogle Scholar
48.Vere-Jones, D. (1967). Ergodic properties of nonnegative matrices I. Pacific Journal of Mathematics, 22(2): 361–386.CrossRefGoogle Scholar
49.Weber, R.R. (1982). Scheduling jobs with stochastic processing requirements on parallel machines to minimize makespan or flowtime. Journal of Applied Probability, 19(1): 167–182.CrossRefGoogle Scholar
50.Woodbury, M.A. (1950). Inverting modified matrices. Memorandum Report, Statistical Research Group, no. 42.Google Scholar
51.Zwart, A.P. & Boxma, O.J. (2000). Sojourn time asymptotics in the M/G/1 processor sharing queue. Queueing Systems, 35(1–4): 141–166.CrossRefGoogle Scholar