Sometimes a theory is interpreted realistically—i.e., as literally true—whereas sometimes a theory is interpreted instrumentalistically—i.e., as merely a convenient device for summarizing, systematizing, deducing, etc., a given body of observable facts. This paper is part of a program aimed at determining the basis on which scientists decide on which of these interpretations to accept a theory. I proceed by examining one case: the nineteenth-century debates about the existence of atoms. I argue that there was a gradual transition from an instrumentalist to a realistic acceptance of the atomic theory, because of gradual increases in its predictive power, the “testedness” of its hypotheses, the “determinateness” of its quantities, and because of resolutions of doubts about the acceptability of its basic explanatory concepts.

The subject of this essay is the dependence of evidential relations on background beliefs and assumptions. In Part I, two ways in which the relation between evidence and hypothesis is dependent on such assumptions are discussed and it is shown how in the context of appropriately differing background beliefs what is identifiable as the same state of affairs can be taken as evidence for conflicting hypotheses. The dependence of evidential relations on background beliefs is illustrated by discussions of the Michelson-Morley experiment and the discovery of oxygen. In Part II, Hempel's analysis of confirmation and the contrasting model of theory acceptance provided by philosophers such as Kuhn and Feyerabend are discussed. It is argued that both are inadequate (on different grounds) and the problems addressed by each are shown to be more satisfactorily approached by means of the analysis developed in Part I. In Part III, it is argued that if there are objective criteria for deciding between competing theories, these cannot be simply that one theory has greater evidential support than another. Finally, some further methodological questions arising from the analysis are mentioned.

I characterize a notion of causal agency that is the causitive component of many transitive verbs. The agency of what I call substantial causes relates objects physically to systems with which they interact. Such agent causation does not reduce to conditionship relations, nor does it cease to play a role in scientific discourse. I argue, contrary to regularity theories, that causal claims do not in general depend for their sense on generalities nor do they entail the existence of laws. Clarification of the relationships among substantial causes, causal processes, and explanatory conditions separates the analysis of causal connection from that of nomological connection. This clarification is then applied to a variety of issues in the analysis of causality.

The theory of general relativity has produced some great insights into the nature of space and time. Unfortunately, its relevance to the problem of the direction of time has been overestimated. This paper points out that the problem of the direction of time can be formulated in purely local ways, and that in this kind of formulation considerations of general relativity are of little or no importance. On the basis of this, positions which assume that relativistic considerations are always relevant are criticised.

It is argued that Hempel's original rejection of the prediction criterion of confirmation in [8] (on the grounds that it leads to a circular definition of confirmation) was ill-conceived, and that his own approach exhibits undesirable consequences to the degree that it deviates from this criterion. A version of the prediction criterion is formulated which, in addition to being-non circular, escapes the criticisms advanced against Hempel's satisfaction criterion, offers certain clear advantages over alternative approaches, and may serve as the basis for a theory of qualitative confirmation. The definition of confirmation developed here violates two of Hempel's three criteria of adequacy, and in showing why it should do so some light is shed on various issues in the debate concerning the acceptability of these criteria.

A detailed analysis is made of Grünbaum's claim that the Abraham-Lorentz (AL) and Dirac-Lorentz (DL) equations have no bearing on causality. It is pointed out that (a) both equations are derived from F = ma, and thus should obey the same causality conditions as Newton's law, (b) independently of what boundary conditions are imposed, non-causal behavior is always along the same straight line as the force, (c) the distinction in status between laws and boundary conditions which Grünbaum imposes is one which is not always useful, especially since what is a law in one formulation of the theory can become a boundary condition in another, and thus it is argued that a complete theory must be such that laws and boundary conditions form a coherent whole, (d) the asymptotic boundary conditions that are applied are in agreement with experiment, (e) the AL equation is such that if the “effect,” the acceleration as function of time, is known, then the “cause,” the force, can be determined. In addition, it is noted that in the DL equation the acceleration at times later than t influences the acceleration at t. Finally, it is pointed out that electrodynamics is indeed a causal field theory, and that retrocausality is due to the transition from a field description to a particle description.

Dirac's classical electrodynamics countenances “preaccelerations” of charged particles at a time t as mathematical functions of external forces applied after the time t. These preaccelerations have been interpreted as evidence for physical retrocausation upon assuming that, in electrodynamics no less than in Newton's second law, external forces sustain an asymmetric causal relation to accelerations. And this retrocausal interpretation has just been defended against the critiques in (Grünbaum 1976), (Grünbaum and Janis, 1977 and 1978) by appeal to the formal assimilation of the electrodynamic laws of motion to Newton's second law. It is argued below that this latest defense of the retrocausal interpretation is even more ill-founded than the prior ones in the literature.

It is usually supposed that the ‘fundamental’ laws of nature must be general, i.e. must essentially begin with a universal quantifier (Hempel and Oppenheim 1965, p. 272). Other ‘derivative’ laws may not satisfy this requirement but only because they are the logical or mathematical consequences of a set of fundamental laws. As it stands, this requirement is either too strong or trivial. Consider the Newtonian gravitational law: 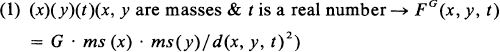where FG(x, y, t) is the impressed gravitational force on x due to y at t, ms(x) is the mass of x, d(x, y, t) is the displacement of the center of mass of x from the center of mass of y at t, and G is the universal gravitational constant. (For simplicity, we ignore the vector nature of FG). What is the role of the constant “G”? Reflection shows that it is actually a disguised existential quantifier, or, more precisely, a Skolem function replacement for one. Rendering Newtonian mechanics in a parsimonious language, we could drop the “G” and rewrite (1) as

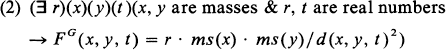
The constant “G” could then be defined, if desired, as the unique r satisfying (2) (the propriety of this definition is guaranteed by (2)). Such a theory would have exactly the same deductive consequences as (1). But (2) has an initial existential quantifier essentially.