No CrossRef data available.
Article contents
Generality and Nomological Form
Published online by Cambridge University Press: 01 April 2022
Extract
It is usually supposed that the ‘fundamental’ laws of nature must be general, i.e. must essentially begin with a universal quantifier (Hempel and Oppenheim 1965, p. 272). Other ‘derivative’ laws may not satisfy this requirement but only because they are the logical or mathematical consequences of a set of fundamental laws. As it stands, this requirement is either too strong or trivial. Consider the Newtonian gravitational law:
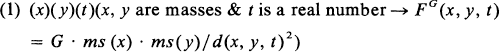 where FG(x, y, t) is the impressed gravitational force on x due to y at t, ms(x) is the mass of x, d(x, y, t) is the displacement of the center of mass of x from the center of mass of y at t, and G is the universal gravitational constant. (For simplicity, we ignore the vector nature of FG). What is the role of the constant “G”? Reflection shows that it is actually a disguised existential quantifier, or, more precisely, a Skolem function replacement for one. Rendering Newtonian mechanics in a parsimonious language, we could drop the “G” and rewrite (1) as
where FG(x, y, t) is the impressed gravitational force on x due to y at t, ms(x) is the mass of x, d(x, y, t) is the displacement of the center of mass of x from the center of mass of y at t, and G is the universal gravitational constant. (For simplicity, we ignore the vector nature of FG). What is the role of the constant “G”? Reflection shows that it is actually a disguised existential quantifier, or, more precisely, a Skolem function replacement for one. Rendering Newtonian mechanics in a parsimonious language, we could drop the “G” and rewrite (1) as
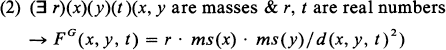
The constant “G” could then be defined, if desired, as the unique r satisfying (2) (the propriety of this definition is guaranteed by (2)). Such a theory would have exactly the same deductive consequences as (1). But (2) has an initial existential quantifier essentially.
- Type
- Discussion
- Information
- Copyright
- Copyright © Philosophy of Science Association 1979


