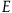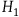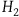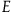1. Introduction
According to Bayesian confirmation theory, a piece of evidence
![]() $E$
confirms two hypotheses
$E$
confirms two hypotheses
![]() ${H_1}$
and
${H_1}$
and
![]() ${H_2}$
individually if and only if
${H_2}$
individually if and only if
![]() $E$
makes each of them more likely to be true (Fitelson Reference Fitelson2001; Strevens Reference Strevens2017). That is, the following two inequalities are satisfied:
$E$
makes each of them more likely to be true (Fitelson Reference Fitelson2001; Strevens Reference Strevens2017). That is, the following two inequalities are satisfied:
This conception of confirmation is perhaps the most popular currently on the market. But it is a well-known fact, presumably first noted by Carnap (Reference Carnap1950), that confirmation, thus understood, does not always agglomerate over conjunction (the label is from Leitgeb Reference Leitgeb2013). That is, condition (1) does not entail that
To see this more clearly, consider sampling a card from a standard deck. Let
![]() $E$
be that the card is red,
$E$
be that the card is red,
![]() ${H_1}$
that it is a heart, and
${H_1}$
that it is a heart, and
![]() ${H_2}$
that it is a diamond (Roche Reference Roche2012). Here, the agglomeration antecedent (1) is satisfied but the consequent (2) is not.Footnote 1
${H_2}$
that it is a diamond (Roche Reference Roche2012). Here, the agglomeration antecedent (1) is satisfied but the consequent (2) is not.Footnote 1
Still, there are conditions under which Bayesian confirmation does agglomerate over conjunction, i.e., conditions under which (1) does entail (2). And in this paper, I would like to present a new one. This new condition will, however, turn out somewhat puzzling. I will introduce it in section 2 and point out in section 3 that a precursor can already be found in the work of Carnap and Salmon. I then discuss an objection in section 4 and examine how the new condition relates to previous agglomeration conditions in section 5. Finally, I conclude in section 6.
2. NOR-confirmation
The new agglomeration condition I would like to present is the following:
Less formally, it states that the evidence in question
![]() $E$
confirms that neither hypothesis
$E$
confirms that neither hypothesis
![]() ${H_1}$
nor
${H_1}$
nor
![]() ${H_2}$
is true, or, equivalently, that both target hypotheses are false. Due to the obvious relationship to Peirce’s (Reference Peirce, Hartshorne and Weiss1933) NOR-connective
${H_2}$
is true, or, equivalently, that both target hypotheses are false. Due to the obvious relationship to Peirce’s (Reference Peirce, Hartshorne and Weiss1933) NOR-connective
![]() ${H_1} \downarrow {H_2}$
, I will call condition (3) NOR-confirmation.
${H_1} \downarrow {H_2}$
, I will call condition (3) NOR-confirmation.
Intuitively, NOR-confirmation (3) is at odds with both the agglomeration antecedent (1) and the consequent (2). After all, the two latter conditions state that the evidence in question
![]() $E$
confirms that both target hypotheses
$E$
confirms that both target hypotheses
![]() ${H_1}$
and
${H_1}$
and
![]() ${H_2}$
are true, namely individually and conjunctively. It might therefore come as a surprise that NOR-confirmation (3) guarantees that agglomeration is valid for Bayesian confirmation. That is, whenever (3) holds, (1) entails (2). For a proof, first observe that (3) is equivalent toFootnote 2
${H_2}$
are true, namely individually and conjunctively. It might therefore come as a surprise that NOR-confirmation (3) guarantees that agglomeration is valid for Bayesian confirmation. That is, whenever (3) holds, (1) entails (2). For a proof, first observe that (3) is equivalent toFootnote 2
which, by general additivity, expands to
By simple algebra, this is equivalent to
and, by condition (1), the following equivalent of (2) follows:
To see that NOR-confirmation (3) is a non-trivial condition for agglomeration, i.e., (3) is consistent with (1), consider an urn containing ten balls with three binary attributes, distributed as shown in Table 1. Let the evidence
![]() $E$
be that a randomly drawn ball is blue,
$E$
be that a randomly drawn ball is blue,
![]() ${H_1}$
that it is small, and
${H_1}$
that it is small, and
![]() ${H_2}$
that it is clean. Then, NOR-confirmation (3) is satisfied, i.e., the evidence confirms that the drawn ball is not small and not clean:
${H_2}$
that it is clean. Then, NOR-confirmation (3) is satisfied, i.e., the evidence confirms that the drawn ball is not small and not clean:
| Dirty | Clean | ||||
|---|---|---|---|---|---|
| Big | Small | Big | Small | Total | |
| Red | 1 | 2 | 2 | 0 | 5 |
| Blue | 2 | 0 | 0 | 3 | 5 |
| Total | 3 | 2 | 2 | 3 | 10 |
The agglomeration antecedent (1) is satisfied, i.e., the evidence confirms that the drawn ball is small and clean individually,
and hence the agglomeration consequent (2) is satisfied, i.e., the evidence confirms that the drawn ball is small and clean conjunctively:
This shows that NOR-confirmation (3) is a non-trivial condition for agglomeration.
3. Carnap and Salmon
The observation that NOR-confirmation (3) and the agglomeration antecedent (1) are consistent is not entirely new: this fact was already noted implicitly by Carnap (Reference Carnap1950) and Salmon (Reference Salmon and Achinstein1983). The two authors discussed examples in which a piece of evidence
![]() $E$
confirms two hypotheses
$E$
confirms two hypotheses
![]() ${H_1}$
and
${H_1}$
and
![]() ${H_2}$
individually while disconfirming their disjunction
${H_2}$
individually while disconfirming their disjunction
![]() ${H_1} \vee {H_2}$
, the latter being equivalent to NOR-confirmation (3). What is new, however, is that this makes Carnap’s and Salmon’s examples rather peculiar instances of agglomeration. To see this more clearly, consider Salmon’s example:
${H_1} \vee {H_2}$
, the latter being equivalent to NOR-confirmation (3). What is new, however, is that this makes Carnap’s and Salmon’s examples rather peculiar instances of agglomeration. To see this more clearly, consider Salmon’s example:
[A] medical researcher finds evidence confirming the hypothesis that Jones is suffering from viral pneumonia and also confirming the hypothesis that Jones is suffering from bacterial pneumonia—yet this very same evidence disconfirms the hypothesis that Jones has pneumonia! It is difficult to entertain such a state of affairs, even as an abstract possibility. (Salmon Reference Salmon and Achinstein1983, section 3)Footnote 3
Salmon found the fact that such situations can arise “shocking and counterintuitive” (Salmon Reference Salmon and Achinstein1983, section 3). But he overlooked that being an instance of agglomeration, it follows that the evidence also confirms the hypothesis that Jones has viral and bacterial pneumonia. Just imagine the following dialogue:
Researcher: Mr. Jones, good to see you! I just received your lab results. I have some good and some bad news for you. The bad news is that the results confirm that you have viral pneumonia; and they also confirm that you have bacterial pneumonia.
Jones: Oh dear! So I have both viral and bacterial pneumonia?! That explains why I feel so miserable!
Researcher: Well, that is not quite what I said, Mr. Jones! In any case, the good news is that the results also confirm that you have neither viral nor bacterial pneumonia.
Jones: Wait, didn’t you just tell me the opposite? Do the results confirm that I have viral and bacterial pneumonia or do they confirm that I don’t?!
Researcher: Well, they confirm both, Mr. Jones, albeit in different ways.
Jones: How can this be? Is there something wrong with the lab results?
Researcher: No, I can assure you that our lab results are flawless and absolutely reliable. In fact, it follows that they also confirm that you have viral and bacterial pneumonia at the same time.
I suspect that most readers will find the researcher’s utterances confusing and unhelpful. Perhaps, some will even question the validity of her inference, arguing that the lab results should disconfirm the hypothesis that Jones has viral and bacterial pneumonia. But the researcher’s inference is valid and everything she says is consistent.Footnote 4
4. The rarity objection
One might try to relativize the phenomenon above by arguing that it is probably very rare. My response to this objection is twofold: I admit that the phenomenon is not very prevalent, but this does not make it less unsettling. More precisely, the conjunctive prevalence of cases where NOR-confirmation (3) and (1) are jointly satisfied is around 2.5%. And the conditional prevalence of cases where NOR-confirmation (3) is satisfied if (1) is satisfied is around 10%. This can be shown using Monte Carlo integration based on 10 million regular probability functions over an algebra generated by three variables (Metropolis and Ulam Reference Metropolis and Ulam1949). The left-hand graph in figure 1 shows how the prevalence stabilizes with increasing number of probability functions.

Figure 1. Prevalence of the NOR-effect (left) and the Simpson-effect (right).
To put these values into context, compare them with Simpson’s (Reference Simpson1951) paradox, a different but similarly puzzling probabilistic phenomenon where a piece of evidence
![]() $E$
confirms a hypothesis
$E$
confirms a hypothesis
![]() $H$
conditional on some assumption
$H$
conditional on some assumption
![]() $X$
and conditional on
$X$
and conditional on
![]() $\neg X$
, but
$\neg X$
, but
![]() $E$
fails to confirm
$E$
fails to confirm
![]() $H$
unconditionally (Sprenger and Weinberger Reference Sprenger, Weinberger and Edward2021). The conjunctive prevalence of such cases is only around 0.83%, and their conditional prevalence is around 3.33%, as shown on the right-hand side of figure 1. But the low prevalence of Simpson’s paradox has not kept researchers from finding the phenomenon unsettling. So, even if cases where NOR-confirmation (3) and the agglomeration antecedent (1) are jointly satisfied are rare, they are prevalent enough to care about.
$H$
unconditionally (Sprenger and Weinberger Reference Sprenger, Weinberger and Edward2021). The conjunctive prevalence of such cases is only around 0.83%, and their conditional prevalence is around 3.33%, as shown on the right-hand side of figure 1. But the low prevalence of Simpson’s paradox has not kept researchers from finding the phenomenon unsettling. So, even if cases where NOR-confirmation (3) and the agglomeration antecedent (1) are jointly satisfied are rare, they are prevalent enough to care about.
5. Previous agglomeration conditions
NOR-confirmation (3) is not the only agglomeration condition for Bayesian confirmation. As Reichenbach (Reference Reichenbach1956) showed in his analysis of common-cause structures, agglomeration is also valid if the evidence screens off both hypotheses from each other:
And, as Falk (Reference Falk1986) pointed out in his discussion of Cohen’s (Reference Cohen1977) corroboration theorem, agglomeration remains valid even if screening-off is relaxed as follows:Footnote 5
Salmon (Reference Salmon and Achinstein1983) uncovered another interesting condition. While agglomeration can also fail for independent hypotheses, it cannot if, additionally, the two target hypotheses are independent conditional on the evidence:
Finally, there are two more recent conditions from the literature on the problem of irrelevant conjunction (Schurz Reference Schurz2022). The first is part of Fitelson’s (Reference Fitelson2002) confirmational irrelevance condition,
and the second is Hawthorne and Fitelson’s (Reference Hawthorne and Fitelson2004) conditional irrelevance condition which states that the evidence is irrelevant for one hypothesis conditional on the other:
Now, interestingly, NOR-confirmation (3) is logically independent of each of the aforementioned conditions (4)–(8). That is, NOR-confirmation (3) is consistent with each of them but neither entails nor is entailed by any of them. A proof of this statement is provided in Appendix A.
Notice, however, that most of these logical independence relationships break down once the agglomeration antecedent (1) is satisfied. More precisely, if (1) holds, then NOR-confirmation (3) is inconsistent with screening-off (4), full independence (6), confirmational irrelevance (7), and conditional irrelevance (8). A proof of this is provided in Appendix B. With these remarks, I close my discussion of NOR-confirmation (3).
6. Conclusion
In this short paper, I have presented a new condition under which Bayesian confirmation agglomerates over conjunction. One might think that such a condition is helpful because it allows us to establish claims about Bayesian confirmation without tedious case-by-case examination (Shogenji Reference Shogenji2003; Roche Reference Roche2012). But the condition presented here is more puzzling than helpful: it is difficult to see why Bayesian confirmation should agglomerate over conjunction whenever the new condition is satisfied. I hope that Bayesian confirmation theorists can help with an explanation.
Appendix
A. Logical independence
The probability distributions provided in Table 2 show that (3) is logically independent of (4) to (8). Under distribution 1, all conditions (3)–(8) are satisfied and thus none of them entails the negation of the other. Under distribution 2, NOR-confirmation (3) is satisfied while none of the other conditions is. And under distribution 3, NOR-confirmation (3) is violated while the other conditions are satisfied.
Table 2. Probability distributions showing that NOR-confirmation (3) is logically independent of (4)–(8)
|
|
|
|
Distribution 1 | Distribution 2 | Distribution 3 |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 1/16 | 1/16 | 2/16 |
| 0 | 0 | 1 | 1/16 | 1/16 | 2/16 |
| 0 | 1 | 0 | 2/16 | 2/16 | 1/16 |
| 0 | 1 | 1 | 2/16 | 2/16 | 1/16 |
| 1 | 0 | 0 | 2/16 | 2/16 | 2/16 |
| 1 | 0 | 1 | 2/16 | 3/16 | 2/16 |
| 1 | 1 | 0 | 3/16 | 3/16 | 3/16 |
| 1 | 1 | 1 | 3/16 | 2/16 | 3/16 |
Distribution 1
Under this distribution, NOR-confirmation (3) is satisfied:
Screening-off (4), and thus relaxed screening-off (5), are satisfied:
We also have
Thus, full independence (6), confirmational irrelevance (7), and also conditional irrelevance (8) are satisfied.
Distribution 2
NOR-confirmation (3) is satisfied:
Screening-off (4), relaxed screening-off (5), and full independence (6) are violated:
Conditional irrelevance (8), and thus confirmational irrelevance (7), are violated:
Distribution 3
NOR-confirmation (3) is violated:
Screening-off (4), and thus relaxed screening-off (5), are satisfied:
We also have
Thus, full independence (6), confirmational irrelevance (7), and also conditional irrelevance (8) are satisfied.
B. Breakdown of logical independence
If the agglomeration antecedent (1) is satisfied, then (3) is no longer logically independent of (4)–(8). More precisely, if (1) holds, then NOR-confirmation (3) and the agglomeration antecedent (1) jointly entail that the evidence
![]() $E$
confirms
$E$
confirms
![]() ${H_1}$
conditional on
${H_1}$
conditional on
![]() ${H_2}$
and that
${H_2}$
and that
![]() $E$
confirms
$E$
confirms
![]() ${H_2}$
conditional on
${H_2}$
conditional on
![]() ${H_1}$
:
${H_1}$
:
The two conditions also entail that the evidence
![]() $E$
disconfirms
$E$
disconfirms
![]() ${H_1}$
conditional on
${H_1}$
conditional on
![]() $\neg {H_2}$
and that
$\neg {H_2}$
and that
![]() $E$
confirms
$E$
confirms
![]() ${H_2}$
conditional on
${H_2}$
conditional on
![]() $\neg {H_1}$
:
$\neg {H_1}$
:
Together with screening-off (4) or full-independence (6), the second condition yields a contradiction. And together with confirmational irrelevance (7), and thus with conditional irrelevance (8), the first condition yields a contradiction.