In this article we derive analytic and Fourier aspects of a Kronecker limit formula for second-order Eisenstein series. Let Γ be any Fuchsian group of the first kind which acts on the hyperbolic upper half-space H such that the quotient Γ\H has finite volume yet is non-compact. Associated to each cusp of Γ\H, there is a classically studied first-order non-holomorphic Eisenstein series E(s, z) which is defined by a generalized Dirichlet series that converges for Re(s) > 1. The Eisenstein series E(s, z) admits a meromorphic continuation with a simple pole at s = 1. Classically, Kronecker’s limit formula is the study of the constant term 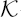 1 (z) in the Laurent expansion of E(s, z) at s = 1. A number of authors recently have studied what is known as the second-order Eisenstein series E*(s, z), which is formed by twisting the Dirichlet series that defines the series E(s, z) by periods of a given cusp form f. In the work we present here, we study an analogue of Kronecker’s limit formula in the setting of the second-order Eisenstein series E* (s, z), meaning we determine the constant term
1 (z) in the Laurent expansion of E(s, z) at s = 1. A number of authors recently have studied what is known as the second-order Eisenstein series E*(s, z), which is formed by twisting the Dirichlet series that defines the series E(s, z) by periods of a given cusp form f. In the work we present here, we study an analogue of Kronecker’s limit formula in the setting of the second-order Eisenstein series E* (s, z), meaning we determine the constant term 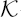 2(z) in the Laurent expansion of E*(s, z) at its first pole, which is also at s = 1. To begin our investigation, we prove a bound for the Fourier coefficients associated to the first-order Kronecker limit function
2(z) in the Laurent expansion of E*(s, z) at its first pole, which is also at s = 1. To begin our investigation, we prove a bound for the Fourier coefficients associated to the first-order Kronecker limit function 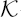 1. We then define two families of convolution Dirichlet series, denoted by
1. We then define two families of convolution Dirichlet series, denoted by 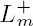 and
and 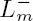 with m ∈ ℕ, which are formed by using the Fourier coefficients of
with m ∈ ℕ, which are formed by using the Fourier coefficients of 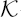 1 and the weight two cusp form f. We prove that for all m,
1 and the weight two cusp form f. We prove that for all m, 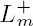 and
and 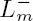 admit a meromorphic continuation and are holomorphic at s = 1. Turning our attention to the second-order Kronecker limit function
admit a meromorphic continuation and are holomorphic at s = 1. Turning our attention to the second-order Kronecker limit function 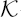 2, we first express
2, we first express 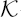 2 as a solution to various differential equations. Then we obtain its complete Fourier expansion in terms of the cusp form f, the Fourier coefficients of the first-order Kronecker limit function
2 as a solution to various differential equations. Then we obtain its complete Fourier expansion in terms of the cusp form f, the Fourier coefficients of the first-order Kronecker limit function 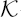 1, and special values
1, and special values 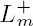 (1) and
(1) and 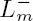 (1) of the convolution Dirichlet series. Finally, we prove a bound for the special values
(1) of the convolution Dirichlet series. Finally, we prove a bound for the special values 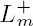 (1) and
(1) and 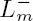 (1) which then implies a bound for the Fourier coefficients of
(1) which then implies a bound for the Fourier coefficients of 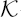 2. Our analysis leads to certain natural questions concerning the holomorphic projection operator, and we conclude this paper by examining certain numerical examples and posing questions for future study.
2. Our analysis leads to certain natural questions concerning the holomorphic projection operator, and we conclude this paper by examining certain numerical examples and posing questions for future study.
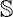 4
4