Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Davis, Christopher
Langer, Andreas
and
Zink, Thomas
2012.
Overconvergent Witt vectors.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2012,
Issue. 668,
p.
1.
Langer, Andreas
and
Zink, Thomas
2015.
Comparison between overconvergent de Rham-Witt and crystalline cohomology for projective and smooth varieties.
Mathematische Nachrichten,
Vol. 288,
Issue. 11-12,
p.
1388.
Matsuue, Hironori
2017.
On relative and overconvergent de Rham–Witt cohomology for log schemes.
Mathematische Zeitschrift,
Vol. 286,
Issue. 1-2,
p.
19.
Lazda, Christopher
and
Pál, Ambrus
2019.
Cycle classes in overconvergent rigid cohomology and a semistable Lefschetz theorem.
Compositio Mathematica,
Vol. 155,
Issue. 5,
p.
1025.


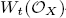 -modules of finite rank endowed with a nilpotent, integrable de Rham-Witt connection. In the case where
-modules of finite rank endowed with a nilpotent, integrable de Rham-Witt connection. In the case where 