Research Article
Une caractérisation des noyaux de convolution rèels de type logarithmique
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 1-49
-
- Article
-
- You have access
- Export citation
On solutions of variational inequalities constrained on a subset of positive capacity
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 51-69
-
- Article
-
- You have access
- Export citation
Completely operator-selfdecomposable distributions and operator-stable distributions
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 71-94
-
- Article
-
- You have access
- Export citation
On a dual relation for addition formulas of additive groups II
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 95-135
-
- Article
-
- You have access
- Export citation
Sur les variétés canoniques de dimension 3 d’indice positif
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 137-167
-
- Article
-
- You have access
- Export citation
On the rank of CM-Type
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 169-172
-
- Article
-
- You have access
- Export citation
On the number of diffeomorphism classes in a certain class of Riemannian manifolds
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. 173-192
-
- Article
-
- You have access
- Export citation
Front Matter
NMJ volume 97 Cover and Front matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. f1-f5
-
- Article
-
- You have access
- Export citation
Back Matter
NMJ volume 97 Cover and Back matter
-
- Published online by Cambridge University Press:
- 22 January 2016, pp. b1-b2
-
- Article
-
- You have access
- Export citation

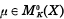 (pour la notation, voir § 2),
(pour la notation, voir § 2),
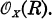 Supposons que R soit numériquement positif et que R
Supposons que R soit numériquement positif et que R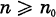 le système linéaire |nR| soit sans point base; en particulier l’anneau
le système linéaire |nR| soit sans point base; en particulier l’anneau 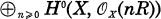 est de type fini sur C.
est de type fini sur C.