We compute the global log-canonical thresholds (lct) of del Pezzo surfaces of degrees ≥ 2 with du Val singularities.

Assuming the Riemann hypothesis, we obtain asymptotic estimates for the mean value of the number of representations of an integer as a sum of two primes. By proving a corresponding Ω-term, we show that our result is essentially the best possible.

We give a bound on embedding dimensions of geometric generic fibers in terms of the dimension of the base, for fibrations in positive characteristic. This generalizes the well-known fact that for fibrations over curves, the geometric generic fiber is reduced. We illustrate our results with Fermat hypersurfaces and genus 1 curves.

We establish that almost all natural numbers n are the sum of four cubes of positive integers, one of which is no larger than n5/36. The proof makes use of an estimate for a certain eighth moment of cubic exponential sums, restricted to minor arcs only, of independent interest.

Quasi-socle ideals, that is, ideals of the form I = Q: mq (q ≥ 2), with Q parameter ideals in a Buchsbaum local ring (A,m), are explored in connection to the question of when I is integral over Q and when the associated graded ring G(I) ⊕ n≥0In/In+1 of I is Buchsbaum. The assertions obtained by Wang in the Cohen-Macaulay case hold true after necessary modifications of the conditions on parameter ideals Q and integers q. Examples are explored.

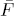For self-injective algebras, Rickard proved that each derived equivalence induces a stable equivalence of Morita type. For general algebras, it is unknown when a derived equivalence implies a stable equivalence of Morita type. In this article, we first show that each derived equivalence F between the derived categories of Artin algebras A and B arises naturally as a functor between their stable module categories, which can be used to compare certain homological dimensions of A with that of B. We then give a sufficient condition for the functor to be an equivalence. Moreover, if we work with finite-dimensional algebras over a field, then the sufficient condition guarantees the existence of a stable equivalence of Morita type. In this way, we extend the classical result of Rickard. Furthermore, we provide several inductive methods for constructing those derived equivalences that induce stable equivalences of Morita type. It turns out that we may produce a lot of (usually not self-injective) finite-dimensional algebras that are both derived-equivalent and stably equivalent of Morita type; thus, they share many common invariants.