Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-23T23:39:37.276Z Has data issue: false hasContentIssue false
  • English
  • Français

Scalar extension of quadratic lattices II

Published online by Cambridge University Press:  22 January 2016

Yoshiyuki Kitaoka
Yoshiyuki Kitaoka*
Affiliation:
Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

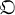Let k be a totally real algebraic number field, the maximal order of k, and let L (resp. M) be a Z-lattice of a positive definite quadratic space U (resp. V) over the field Q of rational numbers. Suppose that there is an isometry σ from 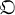L onto 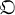M. We have shown that the assumption implies σ(L) = M in some cases in [2]. Our aim in this paper is to improve the results of [2]. In § 1 we introduce the notion of E-type: Let L be a positive definite quadratic lattice over Z.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 67 , August 1977 , pp. 159 - 164
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1977

References

[1] Blichfeldt, H. F., The minimum value of quadratic forms, and the closest packing of spheres, Math. Ann., 101 (1929), 605–608.Google Scholar
[2] Kitaoka, Y., Scalar extension of quadratic lattices, Nagoya Math. J., 66 (1977), 139–149.Google Scholar
[3] Husemoller, J. Milnor-D., Symmetric bilinear forms, Springer-Verlag, 1973.Google Scholar
[4] O’Meara, O. T., Introduction to quadratic forms, Springer-Verlag, 1963.CrossRefGoogle Scholar
[5] Rogers, C. A., Packing and covering, Cambridge University Press, 1964.Google Scholar
[6] Siegel, C. L., Gasammelte Abhandlungen III, Springer-Verlag, 1966.CrossRefGoogle Scholar