Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-16T17:19:59.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Radon-Nikodym Densities between Harmonic Measures on the Ideal Boundary of an Open Riemann Surface

Published online by Cambridge University Press:  22 January 2016

Mitsuru Nakai
Mitsuru Nakai*
Affiliation:
Mathematical Institute, Nagoya University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Resolutive compactification and harmonic measures. Let R be an open Riemann surface. A compact Hausdorff space R* containing R as its dense subspace is called a compactification of R and the compact set Δ = R* -R is called an ideal boundary of R. Hereafter we always assume that R does not belong to the class OG. Given a real-valued function f on Δ, we denote by 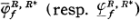the totality of lower bounded superharmonic (resp. upper bounded subharmonic) functions sonis satisfying

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 27 , Issue 1 , February 1966 , pp. 71 - 76
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1966

References

[1] Constantinescu-A, C.. Cornea: Ideale Ränder Riemannscher Flächen, Springer-Verlag, 1963.CrossRefGoogle Scholar