Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T16:11:05.943Z Has data issue: false hasContentIssue false
  • English
  • Français

On the rank of the first radical layer of a p-class group of an algebraic number field

Published online by Cambridge University Press:  22 January 2016

Hiroshi Yamashita
Hiroshi Yamashita*
Affiliation:
Faculty of Business Administry and Information Sciences, Kanazawa Gakuin University, Kanazawa, 920-1302, Japan, [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let p be a prime number. Let M be a finite Galois extension of a finite algebraic number field k. Suppose that M contains a primitive pth root of unity and that the p-Sylow subgroup of the Galois group G = Gal(M/k) is normal. Let K be the intermediate field corresponding to the p-Sylow subgroup. Let 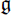= Gal(K/k). The p-class group C of M is a module over the group ring ZpG, where Zp is the ring of p-adic integers. Let J be the Jacobson radical of ZpG. C/JC is a module over a semisimple artinian ring Fp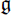. We study multiplicity of an irreducible representation Φ apperaring in C/JC and prove a formula giving this multiplicity partially. As application to this formula, we study a cyclotomic field M such that the minus part of C is cyclic as a ZpG-module and a CM-field M such that the plus part of C vanishes for odd p.

To show the formula, we apply theory of central extensions of algebraic number field and study global and local Kummer duality between the genus group and the Kummer radical for the genus field with respect to M/K.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 156 , 1999 , pp. 85 - 108
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1999

References

[1] Benson, J. D., Representations and cohomology I, Cambrige studies in advanced math. 30, Cambrige, 1991.Google Scholar
[2] Curtis, W. C. and Reiner, I., Methods of representation theory with applications to finite groups and orders, Vol. I, John Wiley & Sons, Inc., 1981.Google Scholar
[3] Greenberg, R., On the Iwasawa invariants of totally real number fields, Amer. J. Math., 98 (1976), 263–284.CrossRefGoogle Scholar
[4] Jehne, W., On knots in algebraic number theory, J. reine angew. Math., 311/312 (1979), 215–254.Google Scholar
[5] Karpilovsky, G., Group representations, Vol I, Part A and Part B, North-Holland math. studies 175, North-Holland, 1992.Google Scholar
[6] Leopoldt, W. H., Zur Struktur der l-Klassengruppe galoissher Zahlkörper, J. reine angew. Math., 199 (1958), 165–174.CrossRefGoogle Scholar
[7] Miyake, K., Central extensions and Schur’s multiplicators of Galois groups, Nagoya Math. J., 90 (1983), 137–144.CrossRefGoogle Scholar
[8] Shirai, S., On the central class field mod m of Galois extensions of algebraic number field, Nagoya Math. J., 71 (1978), 61–85.CrossRefGoogle Scholar
[9] Sinnott, W., On the Stickelberger ideal and the circular units of a cyclotomic field, Ann. of Math., 108 (1978), 107–134.Google Scholar
[10] Yamashita, H., On the Iwasawa invariants of totally real number fields, manuscripta math., 79 (1993), 1–5.CrossRefGoogle Scholar