Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Datskovsky, Boris A.
1996.
On Dirichlet series whose coefficients are class numbers of binary quadratic forms.
Nagoya Mathematical Journal,
Vol. 142,
Issue. ,
p.
95.
Ueno, Takahiko
2001.
Elliptic Modular Forms Arising from Zeta Functions in Two Variables Attached to the Space of Binary Hermitian Forms.
Journal of Number Theory,
Vol. 86,
Issue. 2,
p.
302.
Mizuno, Yoshinori
2012.
Dirichlet series associated with square of class numbers of binary quadratic forms.
Mathematische Zeitschrift,
Vol. 272,
Issue. 3-4,
p.
1115.
Taniguchi, Takashi
and
Thorne, Frank
2013.
OrbitalL-functions for the Space of Binary Cubic Forms.
Canadian Journal of Mathematics,
Vol. 65,
Issue. 6,
p.
1320.
Katsurada, Hidenori
2014.
Explicit formulas for the twisted Koecher–Maaß series of the Duke–Imamoglu–Ikeda lift and their applications.
Mathematische Zeitschrift,
Vol. 276,
Issue. 3-4,
p.
1049.
DIAMANTIS, Nikolaos
and
GOLDFELD, Dorian
2014.
A converse theorem for double Dirichlet series and Shintani zeta functions.
Journal of the Mathematical Society of Japan,
Vol. 66,
Issue. 2,
Miyazaki, Tadashi
Sato, Fumihiro
Sugiyama, Kazunari
and
Ueno, Takahiko
2020.
Converse theorems for automorphic distributions and Maass forms of level N.
Research in Number Theory,
Vol. 6,
Issue. 1,


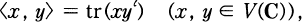
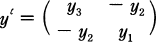 for
for 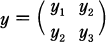 .
.