Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
MATSUMOTO, Keiji
1994.
QUADRATIC IDENTITIES FOR HYPERGEOMETRIC SERIES OF TYPE (k,l).
Kyushu Journal of Mathematics,
Vol. 48,
Issue. 2,
p.
335.
Kita, Michitake
and
Matsumoto, Keiji
1995.
Duality for hypergeometric period matrices.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 71,
Issue. 7,
Aomoto, Kazuhiko
1998.
Open Problems and Conjectures.
Journal of Difference Equations and Applications,
Vol. 4,
Issue. 6,
p.
597.
KACHI, Naoki
MATSUMOTO, Keiji
and
MIHARA, Masateru
1999.
THE PERFECTNESS OF THE INTERSECTION PAIRINGS FOR TWISTED COHOMOLOGY AND HOMOLOGY GROUPS WITH RESPECT TO RATIONAL 1-FORMS.
Kyushu Journal of Mathematics,
Vol. 53,
Issue. 1,
p.
163.
Hanamura, Masaki
and
Yoshida, Masaaki
1999.
Hodge structure on twisted cohomologies and twisted Riemann inequalities I.
Nagoya Mathematical Journal,
Vol. 154,
Issue. ,
p.
123.
Majima, Hideyuki
Matsumoto, Kenji
and
Takayama, Nobuki
2000.
Quadratic relations for confluent hypergeometric functions.
Tohoku Mathematical Journal,
Vol. 52,
Issue. 4,
Yoshida, Masaaki
2000.
Intersection Theory for Twisted Cycles III — Determinant Formulae.
Mathematische Nachrichten,
Vol. 214,
Issue. 1,
p.
173.
OHARA, Katsuyoshi
SUGIKI, Yuichi
and
TAKAYAMA, Nobuki
2003.
Quadratic Relations for Generalized Hypergeometric Functions PFP-1.
Funkcialaj Ekvacioj,
Vol. 46,
Issue. 2,
p.
213.
YOSHIDA, MASAAKI
2003.
A GEOMETRIC INTERPRETATION OF THE SELBERG INTEGRAL.
International Journal of Modern Physics A,
Vol. 18,
Issue. 24,
p.
4343.
Mimachi, Katsuhisa
and
Yoshida, Masaaki
2003.
The reciprocity relation of the Selberg function.
Journal of Computational and Applied Mathematics,
Vol. 160,
Issue. 1-2,
p.
209.
Mimachi, Katsuhisa
and
Yoshida, Masaaki
2004.
Intersection Numbers of Twisted Cycles Associated with the Selberg Integral and an Application to the Conformal Field Theory.
Communications in Mathematical Physics,
Vol. 250,
Issue. 1,
p.
23.
MATSUMOTO, Keiji
2013.
MONODROMY AND PFAFFIAN OF LAURICELLA^|^apos;S FD IN TERMS OF THE INTERSECTION FORMS OF TWISTED (CO)HOMOLOGY GROUPS.
Kyushu Journal of Mathematics,
Vol. 67,
Issue. 2,
p.
367.
GOTO, YOSHIAKI
2013.
TWISTED CYCLES AND TWISTED PERIOD RELATIONS FOR LAURICELLA'S HYPERGEOMETRIC FUNCTION FC.
International Journal of Mathematics,
Vol. 24,
Issue. 12,
p.
1350094.
Goto, Yoshiaki
and
Matsumoto, Keiji
2015.
The monodromy representation and twisted period relations for Appell’s hypergeometric function F4.
Nagoya Mathematical Journal,
Vol. 217,
Issue. ,
p.
61.
Goto, Yoshiaki
and
Matsumoto, Keiji
2015.
The monodromy representation and twisted period relations for Appell’s hypergeometric function F4.
Nagoya Mathematical Journal,
Vol. 217,
Issue. ,
p.
61.
GOTO, Yoshiaki
2015.
INTERSECTION NUMBERS AND TWISTED PERIOD RELATIONS FOR THE GENERALIZED HYPERGEOMETRIC FUNCTION <b><i><sub>m</sub></i></b><b><sub>+</sub></b><sub>1</sub><b><i>F</i></b><b><i><sub>m </sub></i></b>.
Kyushu Journal of Mathematics,
Vol. 69,
Issue. 1,
p.
203.
Goto, Yoshiaki
2017.
Contiguity relations of Lauricella's $F_D$ revisited.
Tohoku Mathematical Journal,
Vol. 69,
Issue. 2,
Mizera, Sebastian
2017.
Combinatorics and topology of Kawai-Lewellen-Tye relations.
Journal of High Energy Physics,
Vol. 2017,
Issue. 8,
Mizera, Sebastian
2018.
Scattering Amplitudes from Intersection Theory.
Physical Review Letters,
Vol. 120,
Issue. 14,
Azevedo, Thales
Chiodaroli, Marco
Johansson, Henrik
and
Schlotterer, Oliver
2018.
Heterotic and bosonic string amplitudes via field theory.
Journal of High Energy Physics,
Vol. 2018,
Issue. 10,


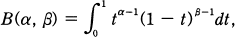
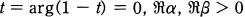 , and the gamma function
, and the gamma function 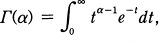
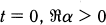 .
.