Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-19T04:03:40.916Z Has data issue: false hasContentIssue false
  • English
  • Français

VIRTUAL ALGEBRAIC FIBRATIONS OF KÄHLER GROUPS

Part of: (Co)homology theory Complex manifolds

Published online by Cambridge University Press:  06 December 2019

STEFAN FRIEDL  and
STEFANO VIDUSSI
STEFAN FRIEDL
Affiliation:
Fakultät für Mathematik, Universität Regensburg, Germany email [email protected]
STEFANO VIDUSSI
Affiliation:
Department of Mathematics, University of California, Riverside, CA 92521, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper stems from the observation (arising from work of Delzant) that “most” Kähler groups 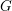$G$ virtually algebraically fiber, that is, admit a finite index subgroup that maps onto 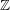$\mathbb{Z}$ with finitely generated kernel. For the remaining ones, the Albanese dimension of all finite index subgroups is at most one, that is, they have virtual Albanese dimension 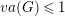$va(G)\leqslant 1$. We show that the existence of algebraic fibrations has implications in the study of coherence and higher BNSR invariants of the fundamental group of aspherical Kähler surfaces. The class of Kähler groups with 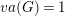$va(G)=1$ includes virtual surface groups. Further examples exist; nonetheless, they exhibit a strong relation with surface groups. In fact, we show that the Green–Lazarsfeld sets of groups with 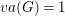$va(G)=1$ (virtually) coincide with those of surface groups, and furthermore that the only virtually RFRS groups with 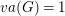$va(G)=1$ are virtually surface groups.

MSC classification

Primary: 32Q55: Topological aspects of complex manifolds 14F35: Homotopy theory; fundamental groups
Type
Article
Information
Nagoya Mathematical Journal , Volume 243 , September 2021 , pp. 42 - 60
Check for updates
Copyright
© 2019 Foundation Nagoya Mathematical Journal

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agol, I., Criteria for virtual fibering, J. Topol. 1(2) (2008), 269–284.10.1112/jtopol/jtn003CrossRefGoogle Scholar
Agol, I., The virtual Haken conjecture, Doc. Math. 18 (2013), 1045–1087; with an appendix by I. Agol, D. Groves and J. Manning.Google Scholar
Amorós, J., Burger, M., Corlette, K., Kotschick, D. and Toledo, D., Fundamental Groups of Compact Kähler Manifolds, Mathematical Surveys and Monographs 44, American Mathematical Society, Providence, RI, 1996.10.1090/surv/044CrossRefGoogle Scholar
Aschenbrenner, M., Friedl, S. and Wilton, H., 3-manifolds Groups, EMS Series of Lectures in Mathematics, European Mathematical Society (EMS), Zürich, 2015.10.4171/154CrossRefGoogle Scholar
Barth, W., Hulek, K., Peters, C. and Van de Ven, A., “Compact complex surfaces”, in Ergebnisse der Mathematik und ihrer Grenzgebiete (3), Folge, Second edition, A Series of Modern Surveys in Mathematics 4, Springer, Berlin, 2004.Google Scholar
Bieri, R., Geoghegan, R. and Kochloukova, D., The sigma invariant of Thompson’s group F, Groups Geom. Dyn. 4(2) (2010), 263–273.10.4171/GGD/83CrossRefGoogle Scholar
Bieri, R., Neumann, W. and Strebel, R., A geometric invariant of discrete groups, Invent. Math. 90(3) (1987), 451–477.10.1007/BF01389175CrossRefGoogle Scholar
Bieri, R. and Renz, B., Valuations on free resolutions and higher geometric invariants of groups, Comment. Math. Helv. 63(3) (1988), 464–497.10.1007/BF02566775CrossRefGoogle Scholar
Bridson, M. R., Howie, J., Miller, C. F. III and Short, H., The subgroups of direct products of surface groups, Geom. Dedicata 92 (2002), 95–103.10.1023/A:1019611419598CrossRefGoogle Scholar
Brudnyi, A., A note on the geometry of Green–Lazarsfeld sets, preprint, 2002, arXiv:math/0204069.Google Scholar
Brudnyi, A., Solvable matrix representations of Kähler groups, Differential Geom. Appl. 19(2) (2003), 167–191.10.1016/S0926-2245(03)00018-4CrossRefGoogle Scholar
Campana, F., Ensembles de Green–Lazarsfeld et quotients résolubles des groupes de Kähler, J. Algebraic Geom. 10(4) (2001), 599–622.Google Scholar
Cartwight, D., Koziark, V. and Yeung, S.-K., On the Cartwight–Steger surface, J. Algebraic Geom. 26(4) (2017), 655–689.10.1090/jag/696CrossRefGoogle Scholar
Cartwright, D. and Steger, T., Enumeration of the 50 fake projective planes, C. R. Acad. Sci. Paris, Ser. 1 348 (2010), 11–13.CrossRefGoogle Scholar
Catanese, F., Moduli and classification of irregular Kähler manifolds (and algebraic varieties) with Albanese general type fibrations, Invent. Math. 104 (1991), 263–289.10.1007/BF01245076CrossRefGoogle Scholar
Catanese, F., Fibred surfaces, varieties isogenous to a product and related moduli spaces, Amer. J. Math. 122(1) (2000), 1–44.10.1353/ajm.2000.0002CrossRefGoogle Scholar
Catanese, F., Fibred Kähler and quasi-projective groups, Adv. Geom. Suppl. (2003), 13–27; Special issue dedicated to Adriano Barlotti.Google Scholar
Catanese, F. and Rollenske, S., Double Kodaira fibrations, J. Reine Angew. Math. 628 (2009), 205–233.Google Scholar
Delzant, T., Trees, valuations and the Green–Lazarsfeld set, Geom. Funct. Anal. 18(4) (2008), 1236–1250.10.1007/s00039-008-0679-2CrossRefGoogle Scholar
Delzant, T., L’invariant de Bieri Neumann Strebel des groupes fondamentaux des variétés kähleriennes, Math. Ann. 348 (2010), 119–125.10.1007/s00208-009-0468-8CrossRefGoogle Scholar
Delzant, T. and Gromov, M., Cuts in Kähler Groups, Progress in Mathematics 248, Birkhäuser, Basel/Switzerland, 2005, 3–55.Google Scholar
Di Cerbo, L. F. and Stover, M., Bielliptic ball quotient compactifications and lattices in PU (2, 1) with finitely generated commutator subgroup, Ann. Inst. Fourier (Grenoble) 67(1) (2017), 315–328.10.5802/aif.3083CrossRefGoogle Scholar
Dimca, A., Papadima, S. and Suciu, A. I., Non-finiteness properties of fundamental groups of smooth projective varieties, J. Reine Angew. Math. 629 (2009), 89–105.Google Scholar
Fiz Pontiveros, G., Glebov, R. and Karpas, I., Virtually fibering random Right-angled Coxeter groups, preprint, 2017.10.1016/j.endm.2018.06.044CrossRefGoogle Scholar
Friedl, S. and Vidussi, S., Rank gradients of infinite cyclic covers of Kähler manifolds, J. Group Theory 19(5) (2016), 941–957.Google Scholar
Green, M. and Lazarsfeld, R., Deformation theory, generic vanishing theorems and some conjectures of Enriques, Catanese and Beauville, Invent. Math. 90(2) (1987), 389–407.10.1007/BF01388711CrossRefGoogle Scholar
Green, M. and Lazarsfeld, R., Higher obstruction to deforming cohomology groups of line bundles, J. Amer. Math. Soc. 4(1) (1991), 87–103.10.1090/S0894-0347-1991-1076513-1CrossRefGoogle Scholar
Hillman, J., Complex surfaces which are fibre bundles, Topology Appl. 100(2–3) (2000), 187–191.10.1016/S0166-8641(98)00085-6CrossRefGoogle Scholar
Hillman, J., Four-Manifolds, Geometries and Knots, Geom. Topol. Monogr. 5, Geom. Topol. Publ., Coventry, 2002, (revision 2014).Google Scholar
Hillman, J., “Sections of surface bundles”, in Interactions between Low-Dimensional Topology and Mapping Class Groups, Geom. Topol. Monogr. 19, Geom. Topol. Publ., Coventry, 2015, 1–19.Google Scholar
Hironaka, E., Alexander stratifications of character varieties, Ann. Inst. Fourier (Grenoble) 47(2) (1997), 555–583.10.5802/aif.1573CrossRefGoogle Scholar
Jankiewicz, K., Norin, S. and Wise, D., Virtually fibering Right-angled Coxeter groups, J. Inst. Math. Jussieu, to appear (2019).CrossRefGoogle Scholar
Johnson, F. E. A., A group theoretic analogue of the Parshin–Arakelov rigidity theorem, Arch. Math. 63 (1994), 354–361.10.1007/BF01189573CrossRefGoogle Scholar
Johnson, F. E. A., “Poly-surface groups”, in Geometry and Cohomology in Group Theory, London Mathematical Society Lecture Note Series 252, Cambridge Univ. Press, Cambridge, 1998, 190–208.10.1017/CBO9780511666131.014CrossRefGoogle Scholar
Kapovich, M., On normal subgroups in the fundamental groups of complex surfaces, preprint, 1998,arXiv:math/9808085.Google Scholar
Kapovich, M., Non-coherence of arithmetic hyperbolic lattices, Geom. Topol. 17 (2013), 39–71.CrossRefGoogle Scholar
Kielak, D., Residually finite rationally-solvable groups and virtual fibring, J. Amer. Math. Soc., to appear (2019).10.1090/jams/936CrossRefGoogle Scholar
Kotschick, D., “On regularly fibered complex surfaces”, in Proceedings of the Kirbyfest (Berkeley, CA, 1998), Geom. Topol. Monogr. 2, 1999, 291–298.Google Scholar
Le, J. A., Lönne, M. and Rollenske, S., Double Kodaira fibrations with small signature, preprint, 2017.Google Scholar
Liu, K., Geometric height inequalities, Math. Res. Lett. 3 (1996), 693–702.10.4310/MRL.1996.v3.n5.a10CrossRefGoogle Scholar
Llosa Isenrich, C., Finite presentations for Kähler groups with arbitrary finiteness properties, J. Algebra 476 (2017), 344–367.10.1016/j.jalgebra.2016.12.011CrossRefGoogle Scholar
Napier, T. and Ramachandran, M., Filtered ends, proper holomorphic mappings of Kähler manifolds to Riemann surfaces, and Kähler groups, Geom. Funct. Anal. 17(5) (2008), 1621–1654.10.1007/s00039-007-0632-9CrossRefGoogle Scholar
Py, P., Coxeter groups and Kähler groups, Math. Proc. Cambridge Philos. Soc. 155 (2013), 557–566.10.1017/S0305004113000534CrossRefGoogle Scholar
Py, P., Some noncoherent, nonpositively curved Kähler groups, Enseign. Math. 62(1–2) (2016), 171–187.10.4171/LEM/62-1/2-10CrossRefGoogle Scholar
Scott, P., The geometries of 3-manifolds, Bull. Lond. Math. Soc. 15 (1983), 401–487.10.1112/blms/15.5.401CrossRefGoogle Scholar
Simpson, C., Subspaces of moduli spaces of rank one local systems, Ann. Sci. Éc. Norm. Super. (4) 26(3) (1993), 361–401.10.24033/asens.1675CrossRefGoogle Scholar
Stallings, J., “On fibering certain 3-manifolds”, in Topology of 3-Manifolds and Related Topics, Prentice-Hall, Englewood Cliffs, NJ, 1962, 95–100.Google Scholar
Stover, M., Cusp and b 1 growth for ball quotients and maps onto ℤ with finitely generated kernel, Indiana Univ. Math. J. (2019), to appear.Google Scholar
Stover, M., On general type surfaces with q = 1 and c 2 = 3p g, Manuscripta Math. 159(1–2) (2019), 171–182.CrossRefGoogle Scholar
Toledo, D., Examples of fundamental groups of compact Kähler manifolds, Bull. Lond. Math. Soc. 22(4) (1990), 339–343.10.1112/blms/22.4.339CrossRefGoogle Scholar
Wise, D., The structure of groups with a quasi-convex hierarchy, Electron. Res. Announc. Math. Sci. 16 (2009), 44–55.Google Scholar
Wise, D., From Riches to RAAGS: 3-Manifolds, Right-angled Artin Groups, and Cubical Geometry, CBMS Regional Conference Series in Mathematics, 117, American Mathematical Society, Providence, RI, 2012.CrossRefGoogle Scholar