Introduction
Stone Age, Copper Age, Bronze Age, Iron Age: We name the eras of mankind after mechanical materials. Is the Metamaterial Age next? Physicists, material scientists, and engineers alike are already working at going beyond (“meta”) what nature has given to us. Significant recent advances in three-dimensional printing on the micro- and macro-scale help them to succeed. The goal is to rationally design and realize tailored artificial media with mechanical characteristics distinct from their constituents to achieve, e.g., effectively stronger, tougher, or lighter materials. In some cases, one can even go beyond what seemed to be fundamental restrictions.
As usual, the mechanics of solid bodies deals with deformations and motions resulting from external forces via Newton's law. For sufficiently small deviations from equilibrium, Hooke's law can be applied. For the paradigm of an elastic Hooke's spring, it simply states that force and extension are proportional. When considering general mechanical materials under arbitrary compression, stretching, and shearing, Hooke's law translates into rank-two tensors for stress and strain, which are connected via the rank-four elasticity tensor (Box 1). Mechanical waves in an isotropic material are an illustrative example. Generally, they can have one longitudinal polarization (like for acoustic sound waves in a gas or fluid) and two orthogonal transverse polarizations (like usually for electromagnetic waves). These three polarizations make elastodynamics even richer than acoustics and electromagnetism.
Box 1. Linear elasticity of mechanical materials.
Mechanical wave propagation
It is amazing how complex the combination of Newton's and Hooke's laws can become when applied to three-dimensional elastic solids.[Reference Rand and Rovenski81–Reference Gould83] In its simplest form, Hooke's law states that the force of a spring is proportional to its extension. In more general, the force turns into the rank-two stress tensor 
$\mathop {\sigma} \limits^{\leftrightarrow }$ and the extension into the rank-two strain tensor 
$\mathop {\epsilon} \limits^{\leftrightarrow }$. The strain is related to the displacement vector 
$\vec u = \vec u(\vec r)$ at position 
$\vec r$ via
$${\epsilon _{lm}} = \displaystyle{1 \over 2}\left( {\displaystyle{{\partial {u_l}} \over {\partial {r_m}}} + \displaystyle{{\partial {u_m}} \over {\partial {r_l}}}} \right).$$
Stress and strain are connected via the rank-four elasticity tensor 
$\mathop {C} \limits^{\leftrightarrow }$, i.e.,
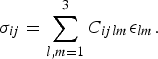$${\sigma _{ij}} = \mathop \sum \limits_{l,m = 1}^3 {C_{ijlm}}{\epsilon _{lm}}. $$
We will review some selected properties of the elasticity tensor below. At finite frequencies, internal resonances may occur, leading to a phase-shifted response of inner masses inside of metamaterial unit cells, which can be expressed by a frequency-dependent mass density ρ(ω). Different resonance frequencies may occur for different oscillation directions, in which case we get a dynamic mass-density tensor 
$\mathop {\rho} \limits^{\leftrightarrow } \left(\omega \right)$. Assuming that 
$\mathop {\rho} \limits^{\leftrightarrow }$ is diagonal (with generally different diagonal elements though), switching to the frequency domain, and exploiting the so-called minor symmetries C ijlm = C ijml, Newton's law becomes
$$ - {\rho _{ii}}{\omega ^2}{u_i} = \mathop \sum \limits_{\,j,l,m = 1}^3 {C_{ijlm}}\displaystyle{{{\partial ^2}{u_l}} \over {\partial {r_j}\; \partial {r_m}}}. $$
Elastostatics corresponds to ω = 0. In elastodynamics, inserting a plane-wave ansatz 
$\vec u = {\vec u\,^0}\exp \left( {{\rm i}\; \vec k \cdot \vec r} \right)$ with wave vector 
$\vec k = \widehat{{\vec k}}\; \left\vert {\vec k} \right\vert = \widehat{{\vec k}}\; k$ leads to the Christoffel equation
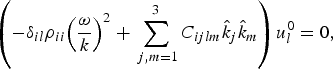$$\left( { - {\delta _{il}}{\rho _{ii}}{{\left( {\displaystyle{\omega \over k}} \right)}^2} + \mathop \sum \limits_{\,j,m = 1}^3 {C_{ijlm}}{{\hat k}_j}{{\hat k}_m}} \right)u_l^0 = 0{\rm,} $$
with Kronecker symbol δ il and phase velocity ω/k. The dispersion relation 
$\vec k(\omega )$ and the three eigenpolarizations 
${\vec u\,^0}$ for each direction 
$\widehat{{\vec k}}$ follow from the Christoffel equation. To describe metamaterials as effective media, the wavelength 2π/k must be much larger than the metamaterial lattice constant (trivially fulfilled in the static case). In general, 
$\vec k$ and 
${\vec u\,^0}$ can include angles different from 0° or 90°. For ordinary materials, where all C ijkl > 0 and ρ ii > 0, (ω/k)2 is positive, hence the wave vector is real, which means that all mechanical waves actually propagate. In contrast, purely imaginary wave vectors corresponding to exponentially decaying contributions result if all C ijkl(ω) > 0 and ρ ii(ω) < 0 or if all C ijkl(ω) < 0 and ρ ii(ω) > 0. If components of the elasticity tensor and of the mass-density tensor are negative simultaneously, various types of unusual backward waves can result—as discussed in this prospective article.
Selected properties of the elasticity tensor
For the mathematical ideal of an isotropic material, the elasticity tensor can be represented by two independent scalar quantities, the choice of which, however, is not unique. The table gives an overview.
Here we have used the so-called Voigt notation C ij = C iijj for i, j = 1,2,3 and C 44 = C 2323.
The relations given in the table remain valid for cubic symmetry, but here three independent scalar quantities are generally needed to represent the elasticity tensor.
Pentamode metamaterials can be cubic, but they are special in that a single scalar quantity, the bulk modulus B (= inverse of the compressibility), suffices to represent the elasticity tensor. In Voigt notation we get
$${C_{ij}} = B\; \forall \; i,j = 1,2,3;\quad {C_{ij}} = 0,\,\,{\rm else}.$$Pentamode metamaterials are sometimes referred to as “meta-liquids”. One should be aware though that the displacement vector, and hence the elasticity tensor, has no meaning for ordinary liquids or gases (as one does not usually track individual particles there)—in sharp contrast to pentamode metamaterials.
Dynamic mass density
For mass-and-spring resonances with eigenfrequencies Ωi inside of the mechanical metamaterial unit cells, the effective behavior can be described by a mass-density tensor with components
$${\rho _{ii}}(\omega ) = \rho + {\rm \Delta} {\rho _i}{\rm \;} \displaystyle{{{\omega ^2}} \over {\Omega _i^2 - {\omega ^2}}}{\rm,} $$where ρ = ρ ii(0) ∀ i is the good old static scalar mass density as measured by a mass balance and Δρ i is a quantity characterizing the oscillator strengths of the resonances. For simplicity, we have omitted damping.
It is hard to say when the first mechanical metamaterial was conceived. However, more than a century ago, Lamb already discussed the possibility of backward waves in vibrating elastic plates.[Reference Lamb1] For a backward wave, mechanical energy and phase fronts move in opposite directions. Today, researchers assign negative refractive indices to such waves and speculate about the possibility of perfect lenses. Materials that expand laterally upon stretching have a negative Poisson's ratio ν and belong to an early class of unusual artificial mechanical materials discovered by Lakes in 1987.[Reference Lakes2] These structures are coined auxetics and can, e.g., be applied in shock absorbers. Auxetics have been reviewed extensively elsewhere[Reference Greaves, Greer, Lakes and Rouxel3] and shall not be in the focus of the present prospective paper. Furthermore, we exclude acoustic metamaterials based on sound propagation in air or liquids, for which solids are often considered as hard-wall boundaries only (see reviews[Reference Moldovan4, Reference Kadic, Bückmann, Schittny and Wegener5]). As outlined in Fig. 1, we do, however, dive into the amazing conceptual and experimental progress regarding light-weight, negative mass density, negative modulus, pentamode, anisotropic mass density, Origami, nonlinear, bistable, and reprogrammable mechanical metamaterials made in recent years.
Figure 1. Overview on mechanical metamaterials. The five rows illustrate (a) auxetic, (b) light-weight, (c) negative-parameter (i.e., negative mass density and/or moduli at finite frequency ω ≠ 0), (d) pentamode, and (e) Origami mechanical metamaterials. The left column shows a combination of the Milton map (bulk modulus B versus shear modulus G) and the Ashby map (one elastic modulus versus mass density ρ). The parameters are zero at the crossing of the three arrows, pointing into the positive directions. In each entry, ordinary solids (black) are compared with the corresponding metamaterials (red). The center column exhibits blueprints of (extended) unit cells highlighting characteristic structural elements, the right column optical or electron micrographs of fabricated structures. These metamaterials can (a) be easily compressible, yet not easily deformable; (b) be light-weight, yet ultrastrong; (c) exhibit complete band gaps or support backward waves; (d) be easily deformable, but not easily compressible; (e) be deployable, light-weight, bistable, and reprogrammable. Applications could be as (a) shock absorbers, (b) support structures, (c) reflectors or concentrators, (d) mechanical cloaks, and (e) structures for space missions. Figures reproduced with permission: (a) © 1987 AAAS; (b) © 2014 PNAS; (c) © 2000 AAAS; (d) © 2012 AIP; (e) © 2014 AAAS.
Light-weight metamaterials
Essentially all ordinary bulk solids have a mass density above ρ ≈ 1000 kg/m3. In order to expand the property space of materials toward very low densities, it is necessary to introduce voids to the material, e.g., as illustrated in Fig. 1(b). Highly regular cellular materials can be designed by the tessellation of a large number of unit cells comprising slender beams, leading to micro-architectured lattice materials, as reviewed in Fleck, Deshpande, and Ashby.[Reference Fleck, Deshpande and Ashby6] Taking this approach to extreme, metallic structures based on hollow beams with mass densities as low as ρ = 0.9 kg/m3 have been realized[Reference Schaedler, Jacobsen, Torrents, Sorensen, Lian, Greer, Valdevit and Carter7] (not counting the air mass in the voids). For comparison, the mass density of air under ambient conditions is ρ = 1.2 kg/m3. The mechanical properties (such as stiffness and strength, i.e., the maximum stress before failure) of such lattice materials are obviously governed by the volume fraction of the constituent material. Moreover, details of the design, in particular the nodal connectivity (or coordination number) of the truss structure have a pronounced influence, too. Deshpande and co-workers demonstrated that, for static loading conditions, two limiting cases of micro-architectured materials can be distinguished, namely bending- and stretching-dominated structures.[Reference Deshpande, Ashby and Fleck8]
Examples for the former are random foams or hexagonal structures. Stretching-dominated structures typically consist of triangulated and octet-truss lattice structures in two and three dimensions, respectively.[Reference Deshpande, Ashby and Fleck9] It has been shown that the normalized effective stiffness of the metamaterial E eff/E 0, with E 0 being the Young's modulus of the parent or constituent material from which the trusses are made, scales according to a power law E eff/E 0 = A(σ eff/ρ 0)b versus the relative density, which is defined as the ratio of the density of the lattice material, ρ eff, to the one of the bulk material ρ 0. The constant A is dimensionless and depends on the geometry of the lattice material and cannot exceed the value of 1. Similarly, the relative strength scales according to σ eff/σ 0 ∝ (ρ eff/ρ 0)c. For bending-dominated lattice materials, one finds b = 3 and c = 2, respectively. These exponents lead to a very unfavorable scaling of the mechanical properties with decreasing density. In contrast, one finds more favorable exponents of b = c = 1 for stretching-dominated materials.[Reference Fleck, Deshpande and Ashby6] It has been demonstrated that octet-truss metamaterials made by projection micro-stereolithography followed by nanoscale coating techniques[Reference Zheng, Lee, Weisgraber, Shusteff, DeOtte, Duoss, Kuntz, Biener, Ge, Jackson, Kucheyev, Fang and Spadaccini10] yield an exponent near b = 1, indeed. The fabricated structures have typical truss diameters of about 50 µm and are either made of solid polymer or alumina, hollow metal, or ceramic tubes. Nevertheless, it is obvious from the equation given above that even for materials with b = 1, the stiffness to density ratio of the metamaterial, E eff/ρ eff, just cannot exceed that of the parent material, E 0/ρ 0, at least as long as E 0 can be considered as constant, i.e., size-independent. Therefore, the term “ultra-stiff”[Reference Zheng, Lee, Weisgraber, Shusteff, DeOtte, Duoss, Kuntz, Biener, Ge, Jackson, Kucheyev, Fang and Spadaccini10] coined for such lattice materials should be taken with a grain of salt.
The Young's modulus of a given material can hardly be altered by changing the size of the components (or the microstructure of the material). In sharp contrast, the effective metamaterial strength can be varied by orders of magnitude. Thus, it is feasible to create ultralight materials with a higher strength-to-stiffness ratio compared with the parent material(s). For metals, such size effects originate from the suppression of dislocation motion or nucleation with decreasing dimensions, as reviewed in.[Reference Kraft, Gruber, Mönig and Weygand11] For brittle materials, the strength is limited by crack nucleation at the largest flaw in the material. On macroscopic length scales, this process can be well described by Weibull statistics. In the nanometer regime, it has been argued that the strength may become insensitive to flaws. It may even reach the limit of theoretical strength,[Reference Gao, Ji, Jäger, Arzt and Fratzl12] as the stress required to nucleate the crack from a flaw increases with decreasing dimensions. This reasoning assumes that the size of the largest flaw does not exceed the smallest dimension of a component, e.g., the thickness of a thin film or a small platelet. Based on this approach, it has been demonstrated that the miniaturization of lattice materials with trusses in the submicron regime creates materials with strength-to-density ratios σ eff/ρ eff exceeding those of ordinary as well as that of engineered cellular materials.[Reference Meza, Das and Greer13–Reference Bauer, Schroer, Schwaiger, Tesari, Lange, Valdevit and Kraft15] The fabrication of these metamaterials has become possible by three-dimensional dip-in direct laser writing of polymer templates.[Reference Bückmann, Stenger, Kadic, Kaschke, Frölich, Kennerknecht, Eberl, Thiel and Wegener16] Subsequently, these templates are coated via atomic-layer deposition of alumina, with layer thicknesses in the range of 10–100 nm.
In[Reference Meza, Das and Greer13] the polymer has been removed after fabrication, and the final lattice structure hence consists of hollow alumina tubes. It was demonstrated that the scaling exponent, c, for the strength for such hollow-tube octet-truss structures is smaller than 2, indicating that it is possible to make use of the stretching-dominated geometry although the trusses are hollow. For such structures, three competing failure mechanisms can be distinguished, including fracture of the tube wall, beam buckling of a truss member, and shell buckling of the tube wall.[Reference Valdevit, Jacobsen, Greer and Carter17] For alumina wall thicknesses <50 nm, the structures showed a significant recoverability from compressive strains as large as 50%. On this basis, it has been argued that local buckling becomes the dominating factor for very thin alumina shells.[Reference Valdevit, Jacobsen, Greer and Carter17]
Bauer et al.[Reference Bauer, Hengsbach, Tesari, Schwaiger and Kraft14] took a somewhat different approach by fabricating lattice materials in which the polymer remains as core inside the trusses. Here, the strength of the structure is limited by local buckling of trusses, which occurs when a stiff alumina shell fails by cracking. The strength of these core–shell polymer–ceramic composites is estimated to be of the order of GPa.[Reference Bauer, Schroer, Schwaiger, Tesari, Lange, Valdevit and Kraft15] The effective strength of these metamaterials reaches up to several 100 MPa.
These examples just touch upon the potential strengths of lattice materials. Nevertheless, they do demonstrate convincingly that the outlined[Reference Fleck, Deshpande and Ashby6] expansion in mechanical property space by design of lattice materials is achievable in reality, especially if one takes advantage of size effects. With foreseeable further improvements regarding three-dimensional micro- and nano-manufacturing, hierarchical micro-architectured light-weight materials with tailored stiffness, strength, and toughness with the “overall macroscopic volumes” required for real-world applications are expected to become available in the near future. So far, these small overall structures should rather be considered as prototypes.
Negative mass densities and negative elastic moduli
Under the static conditions discussed so far, the mass density of a material cannot be negative. Likewise, the elastic moduli must be positive for any stable and unconstrained material. Negative effective parameters are allowed though at finite frequencies near local resonances. These can have small resonance frequencies equivalent to wavelengths much larger than the lattice constant of a periodic metamaterial structure. Under these conditions, a discussion in terms of effective mechanical material parameters is possible. A negative mass density ρ means that an elastic body accelerates out of phase with respect to a harmonically varying driving force. For a negative bulk modulus B, the body would compress upon dynamic stretching. Combining B < 0 and ρ < 0 leads to the counterpart of double-negative or negative-index metamaterials in optics[Reference Kadic, Bückmann, Schittny and Wegener5, Reference Soukoulis and Wegener18] (also see Box 1).
For example, spherical metal cores coated with a compliant rubber shell, packed to a simple-cubic lattice in a host material have been considered early on as depicted in Fig. 1(c).[Reference Liu, Zhang, Mao, Zhu, Yang, Chan and Sheng19] Each core–shell unit forms a simple mass- and spring model, which can exhibit a Mie-type resonance frequency far below the Bragg resonance frequency of the lattice.[Reference Liu, Zhang, Mao, Zhu, Yang, Chan and Sheng19, Reference Huang, Sun and Huang20] Depending of the order of these resonances, negative effective values of the mass density and/or of the elastic moduli can be accomplished. More specifically, numerical predictions have shown that cylindrical or spherical cores embedded into a host material can yield collective Mie oscillations that give rise to negative longitudinal moduli λ + 2G, negative shear moduli G, or negative bulk moduli B.[Reference Wu, Lai and Zhang21] A large material contrast between host material and inclusion helps to obtain pronounced resonances. An additional coating layer can be used to broaden the spectral response—if desired. By combining these designed ingredients, negative refraction and anomalous dispersion can be achieved for specific polarizations. Combined with a negative mass density,[Reference Ding, Liu, Qiu and Shi22, Reference Wu, Lai and Zhang23] the mechanical energy-flow (Poynting) vector points into a direction opposite to that of the phase-velocity vector. Corresponding experiments have used rubber spheres suspended in water[Reference Li and Chan24] (taking advantage of the high-velocity contrast permitting to omit shear contributions) or silicone rubber embedded in a water-based gel host, leading to a negative index of refraction.[Reference Brunet, Merlin, Mascaro, Zimny, Leng, Poncelet, Aristégui and Mondain-Monval25]
Other publications predict a negative bulk modulus transition induced by interplay of different force potentials.[Reference Nicolaou and Motter26]
Furthermore, a chiral route toward negative elastic refraction has lately been discussed.[Reference Varadan, Lakhtakia and Varadan27–Reference Zhu, Liu, Hu, Sun and Huang31] As usual, an object is called chiral if it cannot be brought into congruence with its mirror image by translations and rotations. Helices or screws are paradigms. Chiral or handed media can exhibit activity (like in optics), which means that an incident linear polarization is rotated upon propagation through the medium. Earlier studies suggested the construction of acoustically active media by embedding chiral microstructures in a host material,[Reference Varadan, Lakhtakia and Varadan27–Reference Nagle, Lakhtakia and Thompson29] which have been realized in cellular lattices that exhibit auxetic properties as well.[Reference Tee, Spadoni, Scarpa and Ruzzene30] Other authors have perforated chiral microstructures into thin steel plates and were able to experimentally detect negative refraction of a longitudinally polarized wave.[Reference Zhu, Liu, Hu, Sun and Huang31] By combining dipolar-like and rotational resonances of the oscillating chiral center piece, a collective mode is induced that exhibits both negative effective mass density and negative longitudinal modulus.
Pentamode metamaterials
Transformation optics is a powerful and intuitive design principle,[Reference Milton, Briane and Willis32, Reference Pendry, Schurig and Smith33] which maps fictitious coordinate transformations onto actual material-parameter distributions, thereby achieving specific desired functions. Invisibility cloaking has been a paradigm, because this function appeared impossible for a long time. Unfortunately, the three-dimensional linear elastomechanical equations (see Box 1), unlike the Maxwell equations in electromagnetism, are not form-invariant under general coordinate transformations, at least not for the elasticity tensors of ordinary solids and for scalar mass densities.[Reference Milton, Briane and Willis32] Thus, transformation optics cannot easily be translated to mechanics—neither to the static nor to the dynamic case. Flexural waves in thin plates[Reference Stenger, Wilhelm and Wegener34] or seismic Rayleigh waves on the earth's surface[Reference Brule, Javelaud, Enoch and Guenneau35] are notable exceptions. Both examples are effectively two-dimensional and exhibit a single approximately transverse polarization. The direct lattice-transformation approach[Reference Bückmann, Kadic, Schittny and Wegener36] also uses coordinate transformations for design, however, without making reference to effective mechanical material parameters. So far, this approximate approach has been limited to two-dimensional static situations though.[Reference Bückmann, Kadic, Schittny and Wegener36]
In three dimensions, a solution to the lack of form-invariance in mechanics is based on pentamode metamaterials.[Reference Norris37] Their two-dimensional cousins are bimode metamaterials.[Reference Norris38] Pentamode materials can be represented by a pseudo elasticity tensor with only one non-zero eigenvalue that is of the pure compression type. Loosely speaking, pentamode metamaterials can be seen as meta-liquids or anti-auxetics with G = 0 yet B ≠ 0 (also see Box 1). It is interesting to note in passing that all conceivable linear elasticity tensors of three-dimensional materials can, in principle, be synthesized on the basis of pentamode metamaterials.[Reference Milton and Cherkaev39] Specific three-dimensional microstructures were independently suggested many years ago by Sigmund[Reference Sigmund40] using numerical topology optimization and by Milton and Cherkaev.[Reference Milton and Cherkaev39] Their considerations are analytical and include isotropic as well as anisotropic versions. For the isotropic case, they suggested a lattice of double-cone elements, touching only at singular points. These points form a diamond lattice as illustrated in Fig. 1(d). However, fabrication of corresponding three-dimensional polymer microstructures[Reference Kadic, Bückmann, Stenger, Thiel and Wegener41] has become possible only recently by virtue of three-dimensional dip-in direct laser writing.[Reference Bückmann, Stenger, Kadic, Kaschke, Frölich, Kennerknecht, Eberl, Thiel and Wegener16] Herein, the touching points are approximated by small but finite connections. If their diameter is of the order of 1% of the metamaterial lattice constant, the effective metamaterial bulk modulus B can be more than three orders of magnitude larger than the effective shear modulus G.[Reference Kadic, Bückmann, Stenger, Thiel and Wegener41] Hence, Poisson's ratio comes very close to ν = 0.5 from below. This behavior has been confirmed by static experiments on macroscopic structures[Reference Martin, Kadic, Schittny, Bückmann and Wegener42] and by numerical calculations of the phonon band structure,[Reference Schittny, Bückmann, Kadic and Wegener43] in which the transversely polarized shear modes appear as flat branches. In a large-frequency region, even only a single isotropic longitudinal phonon or vibration mode can be achieved.[Reference Schittny, Bückmann, Kadic and Wegener43]
We note in passing that pentamode behavior with B/G ≫ 1 has also been predicted theoretically for disordered jammed packings of harmonic particles.[Reference Ellenbroek, Zeravcic, van Saarloos and van Hecke44]
Owing to stress concentration close to the double-cone tips, the pentamode metamaterial bulk modulus is mainly determined by the tip diameter. In contrast, the thick part of the double-cones is of much lesser importance.[Reference Kadic, Bückmann, Schittny, Gumbsch and Wegener45] Thus, presently experimentally accessible pentamode metamaterials have volume filling fractions as low as ≈1%, i.e., they can be extremely light-weight (see above). In fact, the mass density can be adjusted largely independently via the diameter of the thick part of the double-cones over a fairly large range. Equivalently, this allows for independently tailoring the phonon phase velocity and wave impedance.[Reference Kadic, Bückmann, Schittny, Gumbsch and Wegener45] Ultra-compliant heavy metamaterials, the opposite of strong ultralight metamaterials discussed above, are an example.
Anisotropic versions of pentamode metamaterials
Anisotropic versions of pentamode[Reference Kadic, Bückmann, Schittny and Wegener46] (and bimode[Reference Layman, Naify, Martin, Calvo and Orris47]) mechanical metamaterials as well as effectively anisotropic laminates composed of isotropic pentamode metamaterials have been considered as well.[Reference Kadic, Bückmann, Schittny, Gumbsch and Wegener45] As in any laminate metamaterial,[Reference Milton48] the anisotropy originates from the layering. If the bulk moduli of the layers are identical, whereas their mass densities are different, an anisotropic dynamic mass-density tensor 
$\mathop {\rho} \limits^{\leftrightarrow }$ arises.[Reference Kadic, Bückmann, Schittny, Gumbsch and Wegener45] Likewise, an anisotropic elasticity tensor 
$\mathop {C} \limits^{\leftrightarrow }$ results for the opposite configuration. This setup has been used for early experimental demonstrations of static elastic (“unfeelability”) cloaking in cylindrical core–shell structures.[Reference Bückmann, Thiel, Kadic, Schittny and Wegener49] Herein, the shell around a massive stiff hollow core has a particular smaller bulk modulus than the surrounding, whereas the mass densities of shell and surrounding are nearly identical.
Effective anisotropy can also be achieved by making the unit cell itself less symmetrical than the three-dimensional pentamode diamond lattice[Reference Kadic, Bückmann, Schittny and Wegener46] (or the two-dimensional hexagonal lattice,[Reference Layman, Naify, Martin, Calvo and Orris47] respectively). For example, one double-cone connection point can be shifted along the space diagonal of the face-centered cubic unit cell.[Reference Milton and Cherkaev39, Reference Kadic, Bückmann, Schittny and Wegener46] However, one should no longer call these structures pentamode (or bimode) because they have less than five (two) easy modes—even for small double-cone connection diameters. Correspondingly, anisotropy is inherently connected to finite shear forces. Maximum anisotropy is even connected to zero Poisson's ratio and a transition toward auxetic behavior.[Reference Kadic, Bückmann, Schittny and Wegener46]
Anisotropic mechanical metamaterials
Crystalline materials rarely exhibit truly isotropic mechanical properties. Even a simple-cubic lattice in the long-wavelength limit generally leads to anisotropic mechanical behavior (also see Box 1). Ideal pentamode metamaterials discussed above are one notable exception, isotropic auxetics with ν = −1 (also coined dilational metamaterials) another one.[Reference Bückmann, Schittny, Thiel, Kadic, Milton and Wegener50] In general, specific anisotropies may be desirable as just discussed for transformation elastodynamics.
Broadly speaking, anisotropic mechanical metamaterials can be realized by laminates,[Reference Milton48] fiber composites, and perforations, to name just a few established concepts. In anisotropic metamaterials, the displacement vectors are not always purely parallel or perpendicular with respect to the propagation wave vector. Thus, the purely longitudinal and the two transverse polarizations of isotropic materials turn into one quasi-longitudinal and two quasi-transverse modes. Anisotropy can be expressed through the stiffness tensor (see Box 1). At finite frequencies, it can also be mapped onto the mass-density tensor 
$\mathop {\rho} \limits^{\leftrightarrow }$, which leads to a modified version of Newton's Second Law.[Reference Milton and Willis51]
Milton and Willis[Reference Milton and Willis51] suggested that an anisotropic mass-density tensor can be created by introducing anisotropy to local resonances in the unit cell (or motif) rather than by the metamaterials translational lattice. A simple example is an oscillating internal mass attached to different Hooke's springs in the three spatial directions.[Reference Bückmann, Kadic, Schittny and Wegener52] Lai and co-workers modified this approach by introducing multiple masses into the unit cell. This crystal with simple-cubic translational lattice exhibits resonances with negative values of the scalar mass density and three independent negative elastic moduli. Depending on the propagation direction of the wave, this structure can mimic a fluid permitting only longitudinal waves or a hybrid fluid–solid behavior with longitudinal and shear wave propagation.[Reference Wu, Lai, Sheng and Zhang53]
Iso-frequency surfaces are an alternative way for illustrating the fingerprint of anisotropic mechanical metamaterial properties. The surface shape depends on the magnitude and the sign of the individual elastic parameters. For mixed signs, hyperbolic dispersion relations result that lead to negative refraction, which has recently been shown experimentally in airborne acoustic metamaterials.[Reference Garcia-Chocano, Christensen and Sanchez-Dehesa54] A prominent application of mechanical metamaterials with hyperbolic dispersion is the so-called hyperlens. Evanescent waves emitted by a subwavelength source are radiated by conversion into propagating elastic waves in the curved hyperlens. Recent experiments[Reference Oh, Seung and Kim55] show that these partial waves can even be magnified and guided toward the far field.
Following the original idea of Milton and Willis, several experimental efforts have worked towards constructing metamaterials with an effectively anisotropic mass-density tensor. Theoretical efforts were devoted to study the elastic response of locally resonant structures consisting of asymmetrically coated elliptical cores embedded in a rigid background. As expected, the in-plane mechanical displacements along the main axes were different. Through modified Newton's law, this behavior can be mapped onto an effectively anisotropic mass-density tensor.[Reference Gu, Luo and Ma56] The same conclusions were reached a few years later for a similar structure through analytical predictions and finite-element calculations.[Reference Liu, Zhu, Liu, Hu and Huang57] Importantly, the mass-density tensor always merges into the good old scalar mass density in the low-frequency limit. Intuitively, at mechanical standstill, the mass of a body has no orientation. These ideas, which were tested in experiments comprising resonators with elliptical micro-perforated coatings, showed good agreement between simulated and measured effective mass densities. Furthermore, transmission measurements for wave propagation along two principal directions demonstrated the existence of band gaps induced by the respective singly negative components of the mass-density tensor.[Reference Zhu, Liu, Huang, Huang and Sun58]
By clamping the mass of the coated core in the aforementioned metamaterial, the mechanical wave behaves just like light in a free-electron Drude metal. In other words, the resonance frequency goes to zero. Equivalently, the effective mass density at low frequencies goes to −∞ and remains negative below a cut-off frequency. This behavior is analogous to that of a membrane in a narrow channel.[Reference Fleury and Alu59] Instead of a channel, a soft solid is filled into the holes of a perforated rigid and immovable material to constitute a mechanical metamaterial with extreme anisotropy.[Reference Yao, Zhou and Hu60] The effective mass-density-tensor component along the perforations is of the above Drude form, whereas the in-plane component goes to +∞ corresponding to an immovable body. These systems have shown their potential for spoof acousto-elastic surface waves and transmission enhancement in thin plates.[Reference Hao, Qiu, Ye, Li, Jia, Ke and Liu61, Reference Christensen, Liang and Willatzen62] The complementary medium composed of rigid bars in a soft background works equally well.[Reference Peng, Qiu, Liu and Wu63] In a similar configuration of square rods in a non-rigid host, one also obtains a complex anisotropy for both, the mass density and the elasticity tensor.[Reference Flores-Mendez and Perez-Rodriguez64]
Origami and programmable metamaterials
Origami is the traditional Asian art of paper folding, Kirigami additionally allows for introducing cuts into the paper. Today, by using free available computer programs such as “TreeMaker”,[Reference Lang65] one can design the Origami folding patterns of almost arbitrary complex three-dimensional structures—including Origami (Kirigami) mechanical metamaterials.[Reference Schenk and Guest66, Reference Castle, Cho, Gong, Jung, Sussman, Yang and Kamien67] Instead of paper, one can likewise start from a thin polymer sheet with indentations defining the creases or from rigid structures with hinges instead of the creases.[Reference Waitukaitis, Menaut, Chen and van Hecke68] Effectively, one can think of the creases as torsional Hooke's springs.[Reference Lechenault, Thiria and Adda-Bedia69] Temperature-responsive polymer-gels instead of paper are yet another option.[Reference Silverberg, Na, Evans, Liu, Hull, Santangelo, Lang, Hayward and Cohen70]
Paper is an inextensible constituent material, yet the metamaterials made thereof can effectively be highly flexible. For the simple example of a one-dimensional accordion folding, it is immediately clear that the Origami metamaterial can be compressed by nearly 100%. The effective elastic moduli, mass density, and wave velocity clearly depend on the degree of compression. In this fashion, the metamaterial properties are tunable. One may even be able to open or close phonon stop bands or band gaps. Additionally, Origami metamaterials are deployable, which is an attractive feature for space applications. Indeed, the famous Miura folding has originally been engineered to deploy satellite solar panels in space.[Reference Miura71] Miura metamaterials can have negative or positive effective Poisson's ratios.[Reference Schenk and Guest66, Reference Wei, Guo, Dudte, Liang and Mahadevan72–Reference Lv, Krishnaraju, Konjevod, Yu and Jiang74] In the assembled state, Origami metamaterials can be extremely light-weight, yet rigid. In principle, most lithographically fabricated metamaterials discussed above could be made by Origami as well.
The nonlinear mechanical properties of Origami metamaterials are even more interesting: One finds bistable behavior of each unit cell.[Reference Silverberg, Na, Evans, Liu, Hull, Santangelo, Lang, Hayward and Cohen70, Reference Silverberg, Evans, McLeod, Hayward, Hull, Santangelo and Cohen73] Switching one cell leads to a defect in the lattice.[Reference Silverberg, Evans, McLeod, Hayward, Hull, Santangelo and Cohen73] Importantly, the effective linear metamaterial mechanical properties around such a stable state can be significantly different for the different stable states. This behavior allows for going beyond tuning[Reference Wang, Casadei, Shan, Weaver and Bertoldi75–Reference Willatzen and Christensen77] in that one can rationally and reversibly choose a stable state. The metamaterial will then stay in that state without further external stimulus (in contrast, pure tuning requires maintaining the stimulus); see Fig. 1(e). In this sense, the metamaterial properties are programmable or reprogrammable[Reference Silverberg, Evans, McLeod, Hayward, Hull, Santangelo and Cohen73] (also see[Reference Waitukaitis, Menaut, Chen and van Hecke68, Reference Florijn, Coulais and van Hecke78, Reference Kang, Shan, Košmrlj, Noorduin, Shian, Weaver, Clarke and Bertoldi79]). If the constituent material had an infinitely large stretching modulus, the Miura folding would exhibit only one degree of freedom[Reference Schenk and Guest66, Reference Miura71]; bistability could not occur. However, real materials can bend and the total energy is the sum of crease and bending energy, allowing for bistable behavior.[Reference Silverberg, Na, Evans, Liu, Hull, Santangelo, Lang, Hayward and Cohen70, Reference Silverberg, Evans, McLeod, Hayward, Hull, Santangelo and Cohen73] A simple example of a building block that exhibits bistable behavior is a circular piece of paper folded once along its diameter. Buckling up or down leads to two stable states.
Conclusions and perspectives
Mechanical metamaterials can be seen as “matter made to order”. Scientists turn into artists or designers when conceiving such artificial solids. The field is simply fun and cool. The resulting properties addressed in this prospective article range from highly strange via extreme to mind-boggling. But will this field really have an impact on our every-day life in the not-too-distant future? A “yes” requires progress with respect to at least two frontiers.
First, fabrication needs another boost. Three-dimensional printing techniques can now make thousands of complex shaped microscopic metamaterial unit cells in reasonable time, but real-world applications likely demand yet more than a thousand times more. Currently, three-dimensional laser-based additive manufacturing attracts huge attention worldwide. Once this technology makes the anticipated jump from prototyping to industrial mass fabrication, mechanical metamaterials could be a huge beneficiary.
Second, “killer” properties and functions may still need to be identified. Have we thought big enough? Has the community focused too much on the linear elastic regime? We have, for example, mentioned mechanical bistability. Bistable switching in the stress–strain curve under strain control corresponds to hysteretic behavior under stress control. Hysteretic behavior means that the metamaterial absorbs energy in one cycle of compression and expansion. The energy is given by the enclosed area. Such mechanical metamaterials could thus be used as reversible shock absorbers, i.e., they would absorb the energy of an impact, yet, unlike for a car bumper, maintain their structural integrity. Ideally, this mechanical nonlinearity would originate exclusively from the metamaterial structure and not from the constituent materials. In this spirit, recent theoretical work has mathematically constructed mechanical metamaterials with any desired nonlinearity of the Poisson's ratio.[Reference Milton80]
In brief, bringing mechanical metamaterials from cool science towards real-world products requires that we keep on working hard and let our imagination fly.
Acknowledgments
We thank Steve Cummer (Duke University), Peter Gumbsch (KIT), Graeme W. Milton (University of Utah), Jose Sanchez-Dehesa (Polytechnical University of Valencia), and Morten Willatzen (Technical University of Denmark) for stimulating discussions. J. C. gratefully acknowledges financial support from the Danish Council for Independent Research and a Sapere Aude grant (no. 12-134776). O. K. is grateful for support by the Robert Bosch foundation. M. W. acknowledges support by the Helmholtz Association through the Program Science and Technology of Nanosystems (STN) and the Karlsruhe School of Optics & Photonics (KSOP). M. K. and M. W. acknowledge support by the Hector Fellow Academy.
Open access
