Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-30T10:53:54.789Z Has data issue: false hasContentIssue false
  • English
  • Français

Novel magnetic arrangement and structural phase transition induced by spin–lattice coupling in multiferroics

Published online by Cambridge University Press:  18 December 2013

Satadeep Bhattacharjee ,
Dovran Rahmedov ,
Laurent Bellaiche  and
Dawei Wang
Satadeep Bhattacharjee
Affiliation:
Department of Physics and Institute for Nanoscience and Engineering, University of Arkansas, Fayetteville, Arkansas 72701
Dovran Rahmedov
Affiliation:
Department of Physics and Institute for Nanoscience and Engineering, University of Arkansas, Fayetteville, Arkansas 72701
Laurent Bellaiche
Affiliation:
Department of Physics and Institute for Nanoscience and Engineering, University of Arkansas, Fayetteville, Arkansas 72701
Dawei Wang
Affiliation:
Electronic Materials Research Laboratory, Key Laboratory of the Ministry of Education and International Center for Dielectric Research, Xi'an Jiaotong University, Xi'an 710049, China
Get access

Abstract

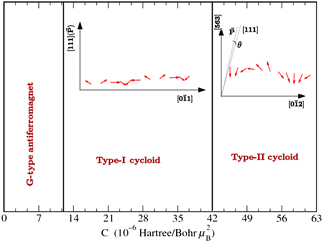
Using an effective Hamiltonian of mutiferroic BiFeO3 (BFO) as a toy model, we explore the effect of the coefficient, C, characterizing the strength of the spin–current interaction, on physical properties. We observe that for larger C values and below a critical temperature, the magnetic moments organize themselves in a novel cycloid, which propagates along a low-symmetry direction and is associated with a structural phase transition from polar rhombohedral to a polar triclinic state. We emphasize that both of these magnetic and structural transitions are results of a remarkable self-organization of different solutions of the spin–current model.

Type
Research Letters
Information
MRS Communications , Volume 3 , Issue 4 , December 2013 , pp. 213 - 218
Copyright
Copyright © Materials Research Society 2013 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Spaldin, N.A. and Fiebig, M.: The renaissance of magnetoelectric multiferroics, Science 309, 391 (2005).CrossRefGoogle ScholarPubMed
2.Ramesh, R. and Spaldin, N.A.: Multiferroics: progress and prospects in thin films, Nature Materials 6, 21 (2007).Google Scholar
3.Wojdel, J.C and Iñiguez, J.: Magnetoelectric response of multiferroic BiFeO3 and related materials from first-principles calculations, Phys. Rev. Lett. 103, 267205 (2009).Google Scholar
4.Wojdel, J.C and Iñiguez, J.: Ab initio indications for giant magnetoelectric effects driven by structural softness, Phys. Rev. Lett. 105, 037208 (2010).Google Scholar
5.Ederer, C. and Fennie, C.J.: Electric-field switchable magnetization via the DzyaloshinskiiMoriya interaction: FeTiO3 versus BiFeO3, J. Phys. Condens. Matter 20, 434219 (2008).Google Scholar
6.Benedek, N.A. and Fennie, C.J.: Hybrid improper ferroelectricity: a mechanism for controllable polarization-magnetization coupling, Phys. Rev. Lett. 106, 107204 (2011).Google Scholar
7.Katsura, H., Nagaosa, N., and Balatsky, A.: Spin current and magnetoelectric effect in noncollinear magnets, Phys. Rev. Lett. 95, 057205 (2005).CrossRefGoogle ScholarPubMed
8.Raeliarijaona, A., Singh, S., Fu, H., and Bellaiche, L.: Predicted coupling of the electromagnetic angular momentum density with magnetic moments, Phys. Rev. Lett. 110, 137205 (2013).Google Scholar
9.Dzyaloshinsky, I.: A thermodynamic theory of weak ferromagnetism of antiferromagnetics, J. Phys. Chem. Solids 4, 241 (1958).Google Scholar
10.Moriya, T.: New mechanism of anisotropic superexchange interaction, Phys. Rev. Lett. 4, 228 (1960).Google Scholar
11.Kimura, T., Goto, T, Shintani, H, Ishizaka, K, Arima, T, and Tokura, Y: Magnetic control of ferroelectric polarization, Nature 426, 55 (2003).Google Scholar
12.Yamasaki, Y., Sagayama, H., Abe, N., Arima, T., Sasai, K., Matsuura, M., Hirota, K., Okuyama, D., Noda, Y., and Tokura, Y.: Cycloidal spin order in the a-axis polarized ferroelectric phase of orthorhombic perovskite manganite, Phys. Rev. Lett. 101, 097204 (2008).Google Scholar
13.Lebeugle, D., Colson, D., Forget, A., Viret, M., Bataille, A. M., and Gukasov, A.: Electric-field-induced spin flop in BiFeO3 single crystals at room temperature, Phys. Rev. Lett. 100, 227602, (2008).Google Scholar
14.Rahmedov, D., Wang, D., Iniguez, J., and Bellaiche, L.: Magnetic cycloid of BiFeO3 from atomistic simulations, Phys. Rev. Lett. 109, 037207 (2012).Google Scholar
15.Sosnowska, I., Loewenhaupt, M., David, W.I.F., and Ibberson, R.M.: Investigation of the unusual magnetic spiral arrangement in BiFeO3, Physica B 180, 117 (1992).Google Scholar
16.Sosnowska, I., Peterlin-Neumaier, T., and Steichele, E.: Spiral magnetic ordering in bismuth ferrite, J. Phys. C Solid State Phys. 15, 4835 (1982).Google Scholar
17.Zalesskii, A.V., Frolov, A.A., Zvezdin, A.K., Gippius, A.A., Morozova, E.N., Khozeevc, D.F., Bush, A.S., and Pokatilov, V.S.: Effect of spatial spin modulation on the relaxation and NMR frequencies of 57Fe nuclei in a ferroelectric antiferromagnet BiFeO3, J. Exp. Theor. Phys. 95, 101 (2002).Google Scholar
18.Zalesskii, A.V., Zvezdin, A.K., Frolov, A.A., and Bush, A.A.: 57Fe NMR study of a spatially modulated magnetic structure in BiFeO3, J. Exp. Theor. Phys. Lett. 71, 465 (2000).Google Scholar
19.Bush, A.A., Gippius, A.A., Zalesskii, A.V., and Morozova, E.N.: 209 Bi NMR spectrum of BiFeO3 in the presence of spatial modulation of hyperfine fields, J. Exp. Theor. Phys. Lett. 78, 389 (2003).CrossRefGoogle Scholar
20.Ramazanoglu, M., Ratcliff II, W., Choi, Y.J., Lee, Seongsu, Cheong, S.-W., and Kiryukhin, V.: Temperature-dependent properties of the magnetic order in single-crystal BiFeO3, Phys. Rev. B 83, 174434 (2011).Google Scholar
21.Sosnowska, I. and Przenioslo, R.: Low-temperature evolution of the modulated magnetic structure in the ferroelectric antiferromagnet BiFeO3, Phys. Rev. B 84, 144404 (2011).Google Scholar
22.Przenioslo, R., Palewicz, A., Regulski, M., Sosnowska, I., Ibberson, R.M., and Knight, K.S.: Does the modulated magnetic structure of BiFeO3 change at low temperatures?, J. Phys. Condens. Matter 18, 2069 (2006).Google Scholar
23.Pokatilov, V.S. and Sigov, A.S.: 57Fe NMR study of multiferroic BiFeO3, J. Exp. Theor. Phys. 110, 440 (2010).Google Scholar
24.Sosnowska, I. and Zvezdin, A.L.: Journal of magnetism and magnetic materials, J. Magn. Magn. Mater. 140–144, 167 (1995).Google Scholar
25.de Sousa, R. and Moore, J.E.: Electrical control of magnon propagation in multiferroic BiFeO3 films, Appl. Phys. Lett. 92, 022514 (2008).CrossRefGoogle Scholar
26.Jeong, J., Goremychkin, E.A., Guidi, T., Nakajima, K., Jeon, Gun Sang, Kim, Shin-Ae, Furukawa, S., Kim, Yong Baek, Lee, Seongsu, Kiryukhin, V., Cheong, S-W., and Park, Je-Geun: Spin wave measurements over the full brillouin zone of multiferroic BiFeO3, Phys. Rev. Lett. 108, 077202 (2012).Google Scholar
27.Catalan, G. and Scott, J.F., Physics and Applications of Bismuth Ferrite, Adv. Mater. 21, 2463 (2009).Google Scholar
28.Zhong, W., Vanderbilt, D., and Rabe, K.M.: First-principles theory of ferroelectric phase transitions for perovskites: the case of BaTiO3, Phys. Rev. B 52, 6301 (1995).Google Scholar
29.Albrecht, D., Lisenkov, S., Ren, Wei, Rahmedov, D., Kornev, Igor A., and Bellaiche, L.: Ferromagnetism in multiferroic BiFeO3 films: a first-principles-based study, Phys. Rev. B 81, 140401 (2010).Google Scholar
30.Ederer, C. and Spaldin, N.: Weak ferromagnetism and magnetoelectric coupling in bismuth ferrite, Phys. Rev. B 71, 060401 (2005).Google Scholar
31.Bellaiche, L., Gui, Z., and Kornev, I.A.: A simple law governing coupled magnetic orders in perovskites, J. Phys. Condens. Matter 24, 312201 (2012).Google Scholar
32.Wang, D., Weerasinghe, J., and Bellaiche, L.: Atomistic molecular dynamic simulations of multiferroics, Phys. Rev. Lett. 109, 067203 (2012).Google ScholarPubMed
33.Ramazanoglu, M., Laver, M., Ratcliff, W. II, Watson, S.M., Chen, W.C., Jackson, A., Kothapalli, K., Lee, Seongsu, Cheong, S.-W., and Kiryukhin, V.: Local weak ferromagnetism in single-crystalline ferroelectric BiFeO3, Phys. Rev. Lett. 107, 207206 (2011).Google Scholar
34.George, A.M., Iñiguez, J., and Bellaiche, L.: Optical phonons associated with the low-temperature ferroelectric properties of perovskite solid solutions, Phys. Rev. B 65, 180301 (2002).CrossRefGoogle Scholar
35.Schmid, H.: Some symmetry aspects of ferroics and single phase multiferroics, J. Phys. Condens. Matter 20, 434201 (2008).Google Scholar
36.Noheda, B., Cox, D.E., Shirane, G., Gonzalo, J.A., Cross, L.E., and Park, S-E.: A monoclinic ferroelectric phase in the Pb(Zr1-xTix)O3 solid solution, Appl. Phys. Lett. 74, 2059 (1999).Google Scholar
37.Kiat, J.-M., Uesu, Y., Dkhil, B., Matsuda, M., Malibert, C., and Calvarin, G.: Monoclinic structure of unpoled morphotropic high piezoelectric PMN-PT and PZN-PT compounds, Phys. Rev. B 65, 064106 (2002).Google Scholar
38.Bellaiche, L., Garcia, A., and Vanderbilt, D.: Finite-temperature properties of Pb(Zr1-xTix)O3 alloys from first principles, Phys. Rev. Lett. 84, 5427 (2000).Google Scholar
39.Bellaiche, L., Garcia, A., and Vanderbilt, D.: Low-temperature properties of Pb(Zr1-xTix)O3 solid solutions, Ferroelectrics 266, 41 (2002).Google Scholar
40.George, A.M., Iñiguez, J., and Bellaiche, L.: Anomalous properties in ferroelectrics induced by atomic ordering, Nature 413, 54 (2001).Google Scholar
41.Iñiguez, J. and Bellaiche, L.: Ab initio design of perovskite alloys with predetermined properties: the case of Pb(Sc0.5Nb0.5)O3, Phys. Rev. Lett. 87, 095503 (2001).Google Scholar
42.Prosandeev, S., Wang, D., Ren, W., Iñiguez, J., and Bellaiche, L.: Novel nanoscale twinned phases in perovskite oxides, Adv. Funct. Mater. 23, 234 (2013).Google Scholar
43.Sando, D., Agbelele, A., Rahmedov, D., Liu, J., Rovillain, P., Toulouse, C., Infante, I.C., Pyatakov, A.P., Fusil, S., Jacquet, E., Carretero, C., Deranlot, C., Lisenkov, S., Wang, D., Le Breton, J-M., Cazayous, M., Sacuto, A., Juraszek, J., Zvezdin, A.K., Bellaiche, L., Dkhil, B., Barthlmy, A., and Bibes, M.: Nature Materials, Nat. Mater. DOI:10.1038/NMAT3629.Google Scholar