Introduction
Nanoparticles exhibit a variety of interesting optical properties.[Reference Novotny and Hecht1] Plasmonic particles support resonances of localized surface plasmons, which result in high field concentration in the proximity of the particles and more efficient manipulation of light at the nanoscale. Nanoparticle assembles, like oligomers and clusters, support a broad range of resonances[Reference Prodan, Radloff, Halas and Nordlander2]; their interplay causes sharp features in the spectra, including the so-called Fano resonances,[Reference Luk'yanchuk, Zheludev, Maier, Halas, Nordlander, Giessen and Chong3] and consequently can be utilized in functional optical elements and metasurfaces. It has been shown that subwavelength plasmonic structures can enhance light–matter interaction[Reference Zhukovsky, Babicheva, Evlyukhin, Protsenko, Lavrinenko and Uskov4, Reference Boulesbaa, Babicheva, Wang, Kravchenko, Lin, Mahjouri-Samani, Jacob, Puretzky, Xiao, Ivanov, Rouleau and Geohegan5] and open up possibilities of a wide range of applications such as optical antennas,[Reference Novotny and Hecht1] photovoltaics,[Reference Atwater and Polman6, Reference Babicheva, Ikhsanov, Zhukovsky, Protsenko, Smetanin and Uskov7] scattering-type near-field optical microscopy,[Reference Babicheva, Gamage, Stockman and Abate8] and others.
Particles arranged in periodic lattices enable even more fascinating properties, and the most prominent effects happen when the period of the array is comparable with the wavelength of nanoparticle resonance. Being in the proximity of single-particle resonance maximum, these lattice resonances strongly modify the spectral profile,[Reference Lamprecht, Schider, Lechner, Ditlbacher, Krenn, Leitner and Aussenegg9–Reference Vecchi, Giannini and Gomez Rivas15] but for an offset to the red part of the single-particle resonance, the lattice resonances appear as additional separate features (Fig. 1). Field enhancement and more efficient scattering that results from lattice resonance excitations[Reference Rodriguez, Abass, Maes, Janssen, Vecchi and Gómez Rivas16–Reference Lozano, Louwers, Rodríguez, Murai, Jansen, Verschuuren and Gómez Rivas21] can find applications in sensors,[Reference Offermans, Schaafsma, Rodriguez, Zhang, Crego-Calama, Brongersma and Gómez Rivas22] nanolasers,[Reference Zhou, Dridi, Suh, Kim, Co, Wasielewski, Schatz and Odom23] light harvesting devices,[Reference Zhukovsky, Babicheva, Uskov, Protsenko and Lavrinenko24, Reference Zhukovsky, Babicheva, Uskov, Protsenko and Lavrinenko25] modulators,[Reference Thackray, Thomas, Auton, Rodriguez, Marshall, Kravets and Grigorenko26] and others. The broad variety of enabled functionalities are highlighted in the recent review,[Reference Wang, Ramezani, Väkeväinen, Törmä, Gómez Rivas and Odom27] dipole coupling of multiple particles in the cell,[Reference Baur, Sanders and Manjavacas28] and multipolar interactions in the surface-lattice resonances in two-dimensional arrays of spheres.[Reference Swiecicki and Sipe29, Reference Swiecicki and Sipe30] Different nanoparticles have been demonstrated to enhance lattice resonances in orthogonal and parallel coupling between particles.[Reference Lin and Yi31–Reference Vitrey, Aigouy, Prieto, García-Martín and Gonzalez35] In the present paper, we are focused on the overview of effects behind the pronounced lattice features, lattices of uncoupled multipoles considered so far,[Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36, Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37] and recently demonstrated multipole coupling in the infinite arrays even under the normal incidence of external light waves.[Reference Babicheva and Evlyukhin38] We envision how the processes of electric and magnetic multipoles interplay, cross-coupling, and resonance induction will enrich the field by bringing both fundamental understandings of the effects and opportunities for practical applications.
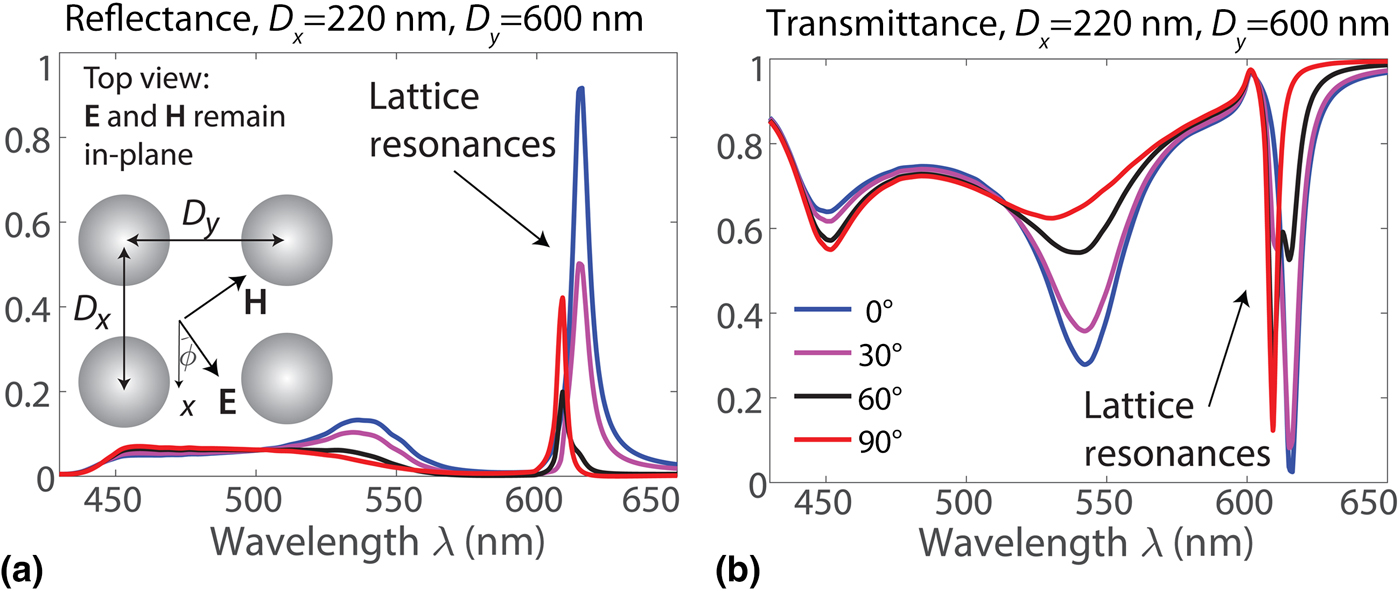
Figure 1. (a) Reflectance and (b) transmittance that show different lattice resonances at the wavelength λ ≈ 610 nm for various polarizations of the incident light. Legend is the same for both panels indicating different angles of polarization ϕ. The lattice periods are D x = 220 nm and D y = 600 nm, and silicon particles have R = 65 nm. Reproduced with permission from Ref. [Reference Babicheva and Evlyukhin43] Copyright (2017) WILEY-VCH Verlag GmbH and Co. KGaA, Weinheim.
Electric-dipole lattice resonances
Dipole coupling in one- and two-dimensional nanoparticle arrays can produce collective lattice resonances, and their wavelengths are determined by the lattice periods. In such electric-dipole (ED) approximation, one needs to take into account only dipole moments of the nanoparticles oriented perpendicular to the lattice direction where the period is comparable with the effective wavelength of the nanoparticle resonance. Under normal incidence of light, every identical spherical nanoparticle arranged in the infinite periodic array has the same effective ED moment p 0 calculated from the equation:
where α p is the ED polarizability, S pp is the ED sum accounting for the electromagnetic interaction between the nanoparticle array, E x(r0) is the electric field of an incident light wave polarized along x-axis located on the array plane, k 0 is the wave number in a vacuum, and ε 0 is the vacuum permittivity. For more details, we referred to Refs. Reference Auguié and Barnes14, Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36, Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37, and in this paper, we consider only the normal incidence of light. Multipole particle polarizabilities, for instance, α p for ED, can be calculated from Mie theory coefficients and the approach is shown for dipoles and quadrupoles in Refs. Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36, Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37.
One can show that the effective polarizability of the particle defined as ![]() $\alpha _{\rm p}^{{\rm eff}} = p_0/E_x$ exhibit singularity at the wavelength close to the period of the structure. In particular, for the case of E x along the x-axis and the wavelength close to Rayleigh anomaly λ ≈ λ RA,eff-1 = D y (transverse period, denoted below as D t), the lattice resonances significantly modify the resonance profile of the particles in the array in comparison with a single particle. At the same time, at the wavelength close to another Rayleigh anomaly λ ≈ λ RA,eff-2 = D x (transverse period, denoted below as D p), only slight changes of the resonance profile take place.
$\alpha _{\rm p}^{{\rm eff}} = p_0/E_x$ exhibit singularity at the wavelength close to the period of the structure. In particular, for the case of E x along the x-axis and the wavelength close to Rayleigh anomaly λ ≈ λ RA,eff-1 = D y (transverse period, denoted below as D t), the lattice resonances significantly modify the resonance profile of the particles in the array in comparison with a single particle. At the same time, at the wavelength close to another Rayleigh anomaly λ ≈ λ RA,eff-2 = D x (transverse period, denoted below as D p), only slight changes of the resonance profile take place.
The case of lattice resonances in dipole approximation has been the most extensively studied so far.[Reference Lamprecht, Schider, Lechner, Ditlbacher, Krenn, Leitner and Aussenegg9–Reference Vecchi, Giannini and Gomez Rivas15] Being mainly observed in the array of plasmonic nanoparticles, it is often referred as “plasmonic” or “surface” lattice resonances. However, as we show below, the resonant feature can be found in many other optical structures and does not necessarily require plasmonic particles, and the deeper study brings us to a much richer variety of effects.
Magnetic-dipole lattice resonances
For the particles supporting magnetic-dipole (MD) resonance, such as silicon nanospheres[Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36, Reference Baryshnikova, Petrov, Babicheva and Belov39, Reference Babicheva, Petrov, Baryshnikova and Belov40] and other simple shapes[Reference Evlyukhin, Reinhardt, Evlyukhin and Chichkov41, Reference Terekhov, Baryshnikova, Artemyev, Karabchevsky, Shalin and Evlyukhin42] or core–shell nanoparticles, one can show the possibility of corresponding lattice effect, and the effective magnetic moment m 0 of identical particles in the arrays can be found as:
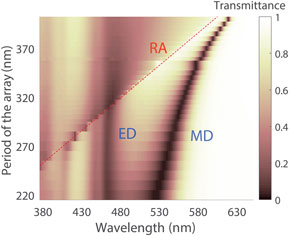
where α m is the MD polarizability, S mm is the MD sum accounting for the electromagnetic interaction between the nanoparticle array, and H y(r0) is the magnetic field of normally incident light wave linearly polarized (with respect to the electric field) along the x-axis. For more details, see Ref. Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36. Thus, similar to EDs, lattice resonances of magnetic counterparts can be spectrally varied, and their wavelength is close to the Rayleigh anomaly λ ≈ λ RA,eff-2 = D p (Fig. 2). As has been shown in the initial work,[Reference Evlyukhin, Reinhardt, Seidel, Luk'yanchuk and Chichkov36] the lattice of particles with ED and MD responses can be described by the system of Eqs. (1) and (2), and the electric (magnetic) dipoles can be considered independently from the magnetic (electric) counterparts that are uncoupled.
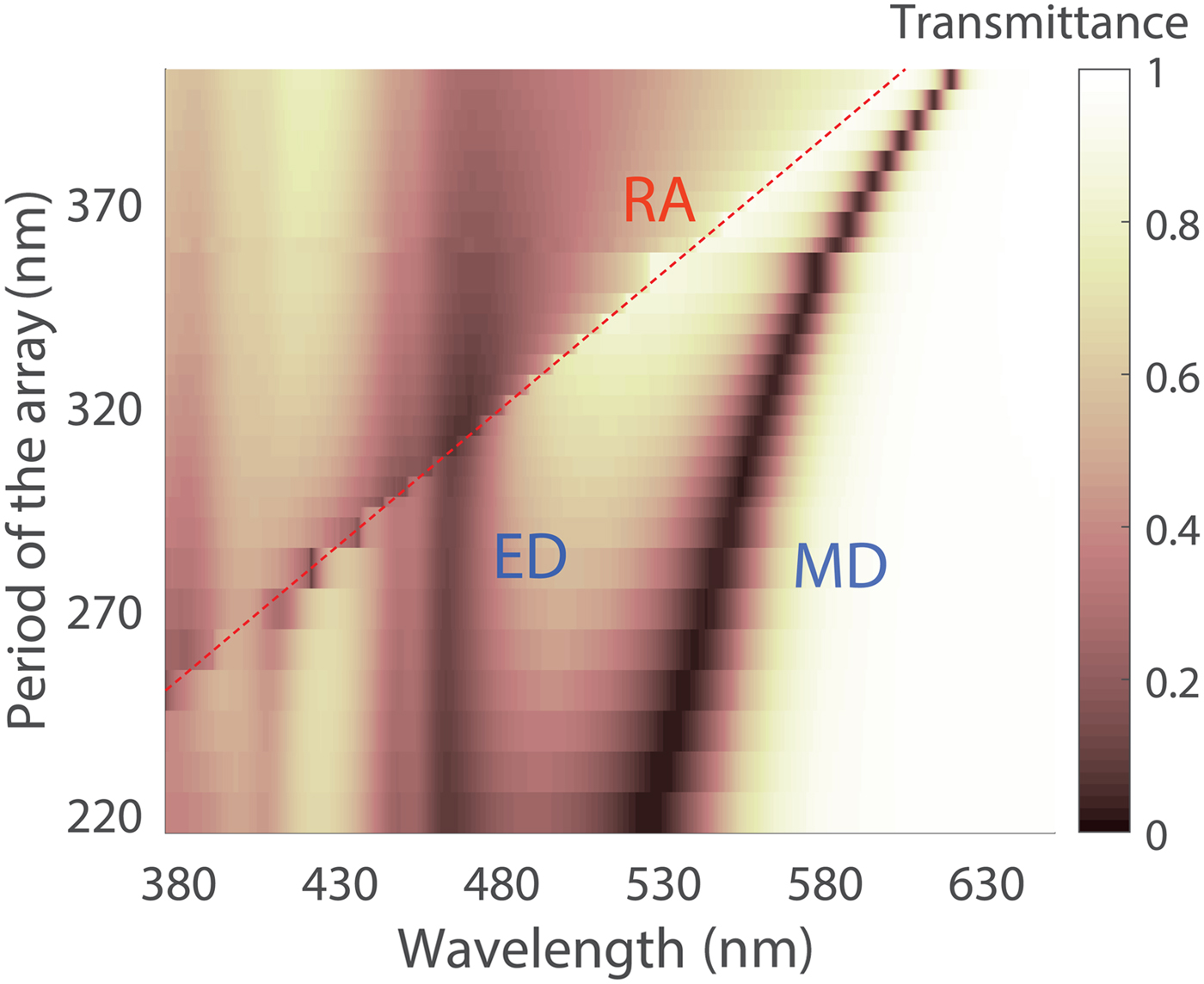
Figure 2. The array transmittance and the change of MD peak resonance wavelength for different periods D p. Silicon nanoparticles have R = 65 nm, and the arrays are in a dielectric matrix with refractive index n = 1.5. Red line shows the wavelength of Rayleigh anomaly (RA). The transverse period is fixed to D t = 220 nm.
We recently studied two-dimensional periodic arrays of silicon and core–shell nanoparticles that support lattice resonances due to the ED and MD resonances of the nanoparticles.[Reference Babicheva and Evlyukhin43] We showed a possibility of achieving a full overlap between the ED and MD nanoparticle resonances adjusting lattice periods independently in each mutual-perpendicular direction. In this way, one can realize the resonant lattice Kerker effect, which is a resonant suppression of the backward-scattered waves (reflectance) from the array. The strong suppression of light reflectance of the structure is appeared due to destructive interference between light scattered by EDs and MDs of every nanoparticle in the backward direction with respect to the incident light wave. The resonant lattice Kerker effect based on the overlap of both ED and MD lattice resonances as well as an experimental proof of independent resonance control[Reference Yang, Yang, Yang, Zhou, Sun, Babicheva and Chen44] have also been demonstrated.
Electric-quadrupole lattice resonances
The particles of larger size and/or complex shape support higher multipoles, and lattice resonances are not limited by the dipole approximation. The case of particles with ED and electric-quadrupole (EQ) resonances has been considered in Ref. Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37. Similar to dipole array, the quadrupoles can be described by the equation:
where α Q is the EQ polarizability, k S is the wave number in the surrounding medium, S QQ is the EQ sum accounting for the electromagnetic interaction between the nanoparticle array, and Q 0 is the matrix element in the particle EQ moment ![]() $\hat Q = Q_0(\hat x\hat z + \hat z\hat x)$.
$\hat Q = Q_0(\hat x\hat z + \hat z\hat x)$.
The work[Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37] has outlined an idea that lattice resonances can be achieved with higher multipole resonances (Fig. 3), which provide broader opportunities for control of resonant features in the structures and designing optical elements based on them. Alike to the case of EDs and MDs, it has been shown that the lattice of EDs and EQs can be described by Eqs. (1) and (3), and they are not coupled to their counterparts.

Figure 3. Extinction cross-section spectra in the dipole σ pext and σ Qext quadrupole approximations calculated per one gold particle of the infinite hexagonal array for the following conditions: normally incident linear polarized optical wave, the radius of the hexagonal cell R S = 600 nm, particle radius R p = 120 nm, and refractive index of the surrounding medium n s = 1.45. Light wavelengths in a vacuum are presented. Reproduced with permission from Ref. [Reference Babicheva and Evlyukhin37] Copyright (2012) American Physical Society.
Multipole coupling in the lattices
The situation drastically changes in the case when the lattice includes a couple of non-zero MD and EQ moments. The equation system describing the lattice with dipole and quadrupole moments under normal incidence of the external light waves is the following:
where S mQ and S Qm are the sums of cross-effects of EQ on MD and MD on EQ, respectively.[Reference Babicheva and Evlyukhin38]
As has been shown recently, the terms S mQ and S Qm are not equal to zero indicating a cross-coupling of MD and EQ in the lattices.[Reference Babicheva and Evlyukhin38] An example of cross-coupling between multipoles is shown in Figs. 4(a) and 4(b). Because of the symmetry of equations with respect to electric and magnetic fields, one can predict the similar effect for ED and MQ: S pM and S Mp are expected to be non-zero and the multipoles in lattice induce each other's resonances in the spectral proximity to Rayleigh anomaly.

Figure 4. (a) Comparison of numerical and semi-analytical calculations of reflectance R 0 and transmittance T 0 for the cases without EQ and MD coupling (“no coupling” in the legend) and with EQ and MD coupling (“with coupling” in the legend). Agreement between semi-analytical calculations and numerical simulations is striking good, and one can see that coupling between EQ and MD multipoles must be taken into account for accurate calculations of resonant profiles. (b) Extinction cross-sections: EQ and MD resonance are excited at the wavelength of Rayleigh anomaly, and these moments make a detrimental contribution to the total extinction cross-section. (c) Transmittance T 0 and T ext. The nanoparticle array with gold spheres of radius R = 100 nm, gold permittivity is taken from experiment [Reference Johnson and Christy53], and the array is in a dielectric matrix with refractive index n = 1.47. Periods are D p = 510 nm and D t = 250 nm.
The array transmission T 0 (calculated for the zeroth diffraction order and accounting for all three moments and their interference) is defined as[Reference Babicheva and Evlyukhin38]
 $$T_0 = \left \vert {1 + \displaystyle{{ik_{\rm S}} \over {2S_{\rm L}}}\left[ {\displaystyle{1 \over {\varepsilon _0\varepsilon _{\rm S}}}\alpha _{\rm p}^{{\rm eff}} + \alpha _{\rm m}^{{\rm eff/coup}} + \displaystyle{{k_0^2} \over {12\varepsilon _0}}\alpha _{\rm Q}^{{\rm eff/coup}}} \right]} \right \vert ^2,$$
$$T_0 = \left \vert {1 + \displaystyle{{ik_{\rm S}} \over {2S_{\rm L}}}\left[ {\displaystyle{1 \over {\varepsilon _0\varepsilon _{\rm S}}}\alpha _{\rm p}^{{\rm eff}} + \alpha _{\rm m}^{{\rm eff/coup}} + \displaystyle{{k_0^2} \over {12\varepsilon _0}}\alpha _{\rm Q}^{{\rm eff/coup}}} \right]} \right \vert ^2,$$
where ![]() $\alpha _{\rm p}^{{\rm eff}} = p_0/E_x$,
$\alpha _{\rm p}^{{\rm eff}} = p_0/E_x$, ![]() $\alpha _{\rm m}^{{\rm eff/coup}} = m_0/H_y$, and
$\alpha _{\rm m}^{{\rm eff/coup}} = m_0/H_y$, and ![]() $\alpha _{\rm Q}^{{\rm eff/coup}} = 2Q_0/(ik_{\rm S}E_x)$ are effective polarizabilities of ED, MD, and EQ, respectively, defined from Eqs. (1) and (4) taking into account coupling between MD and EQ moments; S L = D pD t is the area of one unit cell; ε S is the surrounding medium permittivity.
$\alpha _{\rm Q}^{{\rm eff/coup}} = 2Q_0/(ik_{\rm S}E_x)$ are effective polarizabilities of ED, MD, and EQ, respectively, defined from Eqs. (1) and (4) taking into account coupling between MD and EQ moments; S L = D pD t is the area of one unit cell; ε S is the surrounding medium permittivity.
Signal extinction in the array ![]() $T_{{\rm ext}}$ is defined as
$T_{{\rm ext}}$ is defined as
where ![]() $\sigma _{{\rm ext}}^{\rm p} = ({{k_0} / {\sqrt {\varepsilon _{\rm S}}}} ){\mathop{\rm Im}\nolimits} [\alpha _{\rm p}^{{\rm eff}} ]$,
$\sigma _{{\rm ext}}^{\rm p} = ({{k_0} / {\sqrt {\varepsilon _{\rm S}}}} ){\mathop{\rm Im}\nolimits} [\alpha _{\rm p}^{{\rm eff}} ]$, ![]() $\sigma _{{\rm ext}}^{\rm Q} = (k_0^2 k_{\rm S}/12){\mathop{\rm Im}\nolimits} [\alpha _{\rm Q}^{{\rm eff/coup}} ]$, and
$\sigma _{{\rm ext}}^{\rm Q} = (k_0^2 k_{\rm S}/12){\mathop{\rm Im}\nolimits} [\alpha _{\rm Q}^{{\rm eff/coup}} ]$, and ![]() $\sigma _{{\rm ext}}^{\rm m} = ({{k_0} / {\sqrt {\varepsilon _{\rm S}}}} ){\mathop{\rm Im}\nolimits} [\alpha _{\rm m}^{{\rm eff/coup}} ]$ are extinction cross-sections of ED, MD, and EQ respectively. We note that there is no direct explicit relation between the array transmission T 0 and extinction of signal in the array T ext, but both T 0 and T ext are strongly affected by the lattice effect and have pronounced feature at the wavelength of Rayleigh anomaly [Fig. 4(c)].
$\sigma _{{\rm ext}}^{\rm m} = ({{k_0} / {\sqrt {\varepsilon _{\rm S}}}} ){\mathop{\rm Im}\nolimits} [\alpha _{\rm m}^{{\rm eff/coup}} ]$ are extinction cross-sections of ED, MD, and EQ respectively. We note that there is no direct explicit relation between the array transmission T 0 and extinction of signal in the array T ext, but both T 0 and T ext are strongly affected by the lattice effect and have pronounced feature at the wavelength of Rayleigh anomaly [Fig. 4(c)].
Outlook
In this work, we have shown a dipole–quadrupole model for infinite arrays with identical nanoparticles under normal incidence of light and discussed a coupling between EQ and MD moments resulting in a resonant feature in the proximity to Rayleigh anomaly. Typically, the lattice resonances are narrow in comparison with dipole resonances of a single particle, and because of the high sensitivity of collective resonances to the optical properties of surrounding environment, lattice resonances can be used in sensing applications. For the realistic nanoparticle array with a finite number of particles, parameter deviations, experimental uncertainties, imperfections, and defects, one can expect that lattice resonances will decrease and broaden, or possibly smear out. Previous works on plasmonic nanoparticle arrays had shown that the lattice resonances appear already in the array of about 50 particles and variations in light incidence angle close to the realistic experiments.[Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37, Reference Rodriguez, Schaafsma, Berrier and Gomez Rivas45] Furthermore, lattice resonances and lasing enabled by them have also been shown to persist even upon removing 99% particles from the array.[Reference Schokker and Koenderink46] We would like to emphasize that the considered effect of lattice resonance excitations is expected to be possible for experimental observation as one can predict from the earlier experimental study of lattice resonances in transverse polarizations,[Reference Nikitin47] which has been a motivation of our earlier study.[Reference Babicheva and Evlyukhin38]
The recently demonstrated effect of coupled-multipole lattice resonances has the following implications:
(1) In the case of small multipole excitations of single particles, their arrangement in the periodic array may significantly enhance the multipole's response, induce a magnetoelectric coupling, and result in the resonant spectral features. For instance, the gold nanospheres with the radius down to 80 nm appear to have only ED resonance, but the particle arrangement in the lattice results in EQ collective resonance.[Reference Babicheva and Evlyukhin38]
(2) In the case when only one multipole in the couple ED–MQ or MD–EQ is pronounced and another one is insignificant yet non-zero, the small multipole excitation can be enhanced by the counterpart. For instance, it has been shown that in the array of gold nanospheres with a radius of 100 nm, the lattice resonance is affected not only by EQ but also lattice-induced MD (see Fig. 4 and Ref. Reference Babicheva and Evlyukhin38, compare calculations with and without taking into account multipoles coupling to the ab initio full-wave simulations). Thus, lattice resonances induce a magnetic response from the array of particles without pronounced magnetic moment.
(3) Lattice-induced multipole resonances can be strong enough to have their contribution to the reflection and transmission of the array comparable with the one single-particle dipole resonance. It can result in satisfying generalized Kerker condition and suppression of reflection from the array.[Reference Babicheva and Evlyukhin38] This opens up the possibility for more efficient control of reflective and transmissive properties of the arrays with a variety of multipoles,[Reference Babicheva48, Reference Babicheva49] resonant suppression of reflection and transmission increase, as well as designs of perfect absorbers for light-harvesting devices.
(4) In the realistic experimental structure and the arrays of a finite number of particles, the coupling between particle multipole moments can be stronger and result in a lattice resonance in a broad spectral range because of the boundary effects.[Reference Evlyukhin, Reinhardt, Zywietz and Chichkov37] It has been shown recently that periodic arrays with about 50 particles arranged in square lattice enable not only well-pronounced lattice resonances but also provide an opportunity for their overlap with particle resonances resulting in resonant lattice Kerker effect.[Reference Babicheva and Evlyukhin43]
In the model above, we have considered waves scattered by the particles in the uniform surrounding medium. One can speculate that the periodic array of nanoholes in the film may exhibit properties similar to the nanoparticle array. While each hole can be considered as a scattering element and counterpart of nanoparticle scatterer, the system that includes nanoholes has a much higher level of complexity. For the thin films, it involves free-space waves propagating in the ambient medium on top and bottom sides of the film, surface waves propagating on each interface of the film and ambient medium, as well as other waves that may be supported by the film, such as guided or evanescent within the bulk part of the film.[Reference Barnes, Dereux and Ebbesen50–Reference Lezec and Thio52] This type of system requires a separate detailed study and may be a topic of the future investigation.
Acknowledgments
The authors acknowledge financial support from the Deutsche Forschungsgemeinschaft (Germany), the project EV 220/2-1. The numerical studies have been supported by the Russian Science Foundation (Russian Federation), the project 16-12-10287. This material is based upon work supported by the Air Force Office of Scientific Research under Grant No. FA9550-16-1-0088.