Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-30T10:54:10.137Z Has data issue: false hasContentIssue false
  • English
  • Français

Impact of angular deviation from coincidence site lattice grain boundaries on hydrogen segregation and diffusion in α-iron

Published online by Cambridge University Press:  29 August 2018

Mohamed H. Hamza ,
Mohamed A. Hendy ,
Tarek M. Hatem  and
Jaafar A. El-Awady
Mohamed H. Hamza
Affiliation:
Department of Mechanical Engineering, Whiting School of Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
Mohamed A. Hendy
Affiliation:
Centre for Simulation Innovation and Advanced Manufacturing, the British University in Egypt, Cairo 11837, Egypt
Tarek M. Hatem*
Affiliation:
Centre for Simulation Innovation and Advanced Manufacturing, the British University in Egypt, Cairo 11837, Egypt Faculty of Energy and Environmental Engineering, The British University in Egypt, Cairo 11837, Egypt
Jaafar A. El-Awady
Affiliation:
Department of Mechanical Engineering, Whiting School of Engineering, Johns Hopkins University, Baltimore, MD 21218, USA
*
Address all correspondence to Tarek M. Hatem at [email protected]
Get access

Abstract

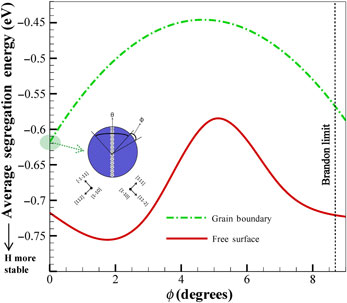
Coincidence site lattice (CSL) grain boundaries (GBs) are believed to be low-energy, resistant to intergranular fracture, as well as to hydrogen embrittlement. Nevertheless, the behavior of CSL-GBs are generally confused with their angular deviations. In the current study, the effect of angular deviation from the perfect $\Sigma 3(111)[1\bar 10]$ GBs in α-iron on the hydrogen diffusion and the susceptibility of the GB to hydrogen embrittlement is investigated through molecular static and dynamics simulations. By utilizing Rice–Wang model, it is shown that the ideal GB shows the highest resistance to decohesion below the hydrogen saturation limit. Finally, the hydrogen diffusivity along the ideal GB is observed to be the highest.

Type
Research Letters
Information
MRS Communications , Volume 8 , Issue 3 , September 2018 , pp. 1197 - 1203
Check for updates
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Barnoush, A. and Vehoff, H.: Recent developments in the study of hydrogen embrittlement: hydrogen effect on dislocation nucleation. Acta Mater. 58, 5274–5285 (2010).Google Scholar
2.McMahon, C.J.: Hydrogen-induced intergranular fracture of steels. Eng. Fract. Mech. 68, 773–788 (2001).Google Scholar
3.Song, J. and Curtin, W.A.: Atomic mechanism and prediction of hydrogen embrittlement in iron. Nat. Mater. 12, 145–151 (2013).Google Scholar
4.Seita, M., Hanson, J.P., Gradečak, S., and Demkowicz, M.J.: The dual role of coherent twin boundaries in hydrogen embrittlement. Nat. Commun. 6, 1–6 (2015).Google Scholar
5.Herbig, M., Raabe, D., Li, Y.J., Choi, P., Zaefferer, S., and Goto, S.: Atomic-scale quantification of grain boundary segregation in nanocrystalline material. Phys. Rev. Lett. 112, 126103 (2014).Google Scholar
6.Wright, S.I. and Larsen, R.J.: Extracting twins from orientation imaging microscopy scan data. J. Microsc. 205, 245–252 (2002).Google Scholar
7.Song, J. and Curtin, W.A.: A nanoscale mechanism of hydrogen embrittlement in metals. Acta Mater. 59, 1557–1569 (2011).Google Scholar
8.Solanki, K.N., Tschopp, M.A., Bhatia, M.A., and Rhodes, N.R.: Atomistic investigation of the role of grain boundary structure on hydrogen segregation and embrittlement in α-fe. Metall. Mater. Trans. A 44, 1365–1375 (2013).Google Scholar
9.Rajagopalan, M., Tschopp, M.A., and Solanki, K.N.: Grain boundary segregation of interstitial and substitutional impurity atoms in alpha-iron. JOM 66, 129–138 (2014).Google Scholar
10.Kimizuka, H., Mori, H., and Ogata, S.: Effect of temperature on fast hydrogen diffusion in iron: a path-integral quantum dynamics approach. Phys. Rev. B 83, 094110 (2011).Google Scholar
11.Liu, X., Xie, W., Chen, W., and Zhang, H.: Effects of grain boundary and boundary inclination on hydrogen diffusion in α-iron. J. Mater. Res. 26, 2735–2743 (2011).Google Scholar
12.Plimpton, S.: Fast parallel algorithms for short-range molecular dynamics. J. Comput. Phys. 117, 1–19 (1995).Google Scholar
13.Ramasubramaniam, A., Itakura, M., and Carter, E.A.: Interatomic potentials for hydrogen in α–iron based on density functional theory. Phys. Rev. B 79, 174101 (2009).Google Scholar
14.Tschopp, M.A. and McDowell, D.L.: Structures and energies of σ 3 asymmetric tilt grain boundaries in copper and aluminium. Philos. Mag. 87, 3147–3173 (2007).Google Scholar
15.Yuan, G., Wei, Z., and Li, G.: A modified polak–ribière–polyak conjugate gradient algorithm for nonsmooth convex programs. J. Comput. Appl. Math. 255, 86–96 (2014).Google Scholar
16.Mendelev, M.I., Han, S., Srolovitz, D.J., Ackland, G.J., Sun, D.Y., and Asta, M.: Development of new interatomic potentials appropriate for crystalline and liquid iron. Philos. Mag. 83, 3977–3994 (2003).Google Scholar
17.Brandon, D.G.: The structure of high-angle grain boundaries. Acta Metall. 14, 1479–1484 (1966).Google Scholar
18.Bhattacharya, S.Kr, Tanaka, S., Shiihara, Y., and Kohyama, M.: Ab initio study of symmetrical tilt grain boundaries in bcc fe: structural units, magnetic moments, interfacial bonding, local energy and local stress. J. Phys. Condens. Matter 25, 135004 (2013).Google Scholar
19.Hamza, M., Hatem, T.M., Raabe, D., and El-Awady, J.A.: Hydrogen diffusion and segregation in alpha iron 3 (111) grain boundaries. In ASME 2015 International Mechanical Engineering Congress and Exposition, pages V009T12A069–V009T12A069. American Society of Mechanical Engineers, 2015.Google Scholar
20.Beck, W., Bockris, J.O'M., McBreen, J., and Nanis, L.: Hydrogen permeation in metals as a function of stress, temperature and dissolved hydrogen concentration. Proc. R. Soc. London Ser. A 290, 220–235 (1966).Google Scholar
21.Quick, N.R. and Johnson, H.H.: Hydrogen and deuterium in iron, 49506c. Acta Metall. 26, 903–907 (1978).Google Scholar
22.Nagano, M., Hayashi, Y., Ohtani, N., Isshiki, M., and Igaki, K.: Hydrogen diffusivity in high purity alpha iron. Scr. Metall. 16, 973–976 (1982).Google Scholar
23.Zhu, D. and Oda, T.: Trap effect of vacancy on hydrogen diffusivity in bcc-fe. J. Nucl. Mater. 469, 237–243 (2016).Google Scholar
24.Katzarov, I.H., Pashov, D.L., and Paxton, A.T.: Fully quantum mechanical calculation of the diffusivity of hydrogen in iron using the tight-binding approximation and path integral theory. Phys. Rev. B 88, 054107 (2013).Google Scholar
25.Kiuchi, K. and McLellan, R.B.: The solubility and diffusivity of hydrogen in well-annealed and deformed iron. Acta Metall. 31, 961–984 (1983).Google Scholar
26.Di Stefano, D., Mrovec, M., and Elsässer, C.: First-principles investigation of quantum mechanical effects on the diffusion of hydrogen in iron and nickel. Phys. Rev. B 92, 224301 (2015).Google Scholar
27.Rice, J.R. and Wang, J.-S.: Embrittlement of interfaces by solute segregation. Mater. Sci. Eng. A 107, 23–40 (1989).Google Scholar
28.Zhong, L., Wu, R., Freeman, A.J., and Olson, G.B.: Charge transfer mechanism of hydrogen-induced intergranular embrittlement of iron. Phys. Rev. B 62, 13938 (2000).Google Scholar
29.Yamaguchi, M., Shiga, M., and Kaburaki, H.: First-principles study on segregation energy and embrittling potency of hydrogen in niσ5 (012) tilt grain boundary. J. Phys. Soc. Japan 73, 441–449 (2004).Google Scholar
30.Krom, A.H.M. and Bakker, A.D.: Hydrogen trapping models in steel. Metall. Mater. Trans. B 31, 1475–1482 (2000).Google Scholar
Supplementary material: PDF

Hamza et al. supplementary material

Figures S1-S3

Download Hamza et al. supplementary material(PDF)
PDF 186.2 KB