Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-30T10:49:42.787Z Has data issue: false hasContentIssue false
  • English
  • Français

A flexible model for instrumented indentation of viscoelastic–plastic materials

Published online by Cambridge University Press:  15 March 2018

Robert F. Cook Open the ORCID record for Robert F. Cook [Opens in a new window]
Robert F. Cook*
Affiliation:
Materials Measurement Science Division, National Institute of Standards and Technology, Gaithersburg, MD 20899, USA
*
Address all correspondence to Robert F. Cook at [email protected]
Get access

Abstract

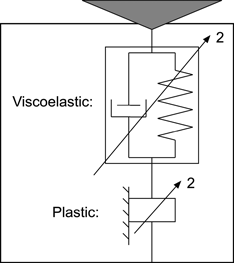
The time-dependent pyramidal or conical indentation of viscoelastic–plastic materials, such as glassy polymers, is examined by a flexible, Kelvin-like model. The model equation is simply solved numerically for a wide range of material properties and indentation loading sequences. The flexibility of the model is demonstrated by generating typical indentation responses for a metal, a ceramic, an elastomer, and a glassy polymer. Polymer indentation is further examined under ramp, hold, and cyclic loading conditions, including adhesive effects. The model and approach should be particularly useful in identifying the various deformation components contributing to observed instrumented indentation phenomena.

Type
Research Letters
Information
MRS Communications , Volume 8 , Issue 2 , June 2018 , pp. 586 - 590
Check for updates
Copyright
Copyright © Materials Research Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Gayle, A.J. and Cook, R.F.: Mapping viscoelastic and plastic properties of polymers and polymer-nanotube composites using instrumented indentation. J. Mater. Res. 31, 2347 (2016). There is a typographical error in Eq. A5: the exponential within the integral should not contain a minus sign.CrossRefGoogle Scholar
2.Tabor, D.: The Hardness of Metals (Oxford University Press, London, England, 1951), pp. 95–114.Google Scholar
3.Lawn, B.R. and Howes, V.R.: Elastic recovery at hardness indentations. J. Mater. Sci. 16, 2745 (1981).CrossRefGoogle Scholar
4.Oliver, W.C. and Pharr, G.M.: An improved technique for determining hardness and elastic-modulus using load and displacement sensing indentation experiments. J. Mater. Res. 7, 1564 (1992).CrossRefGoogle Scholar
5.Cook, R.F. and Oyen, M.L.: Nanoindentation behavior and mechanical properties measurement of polymeric materials. Int. J. Mater. Res. 98, 370 (2007).CrossRefGoogle Scholar
6.Maugis, D.: Contact. Adhesion and Rupture of Elastic Solids. (Springer-Verlag Berlin Heidelberg, Germany, 2000) pp. 283.CrossRefGoogle Scholar