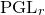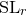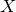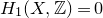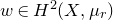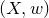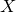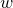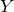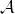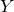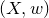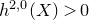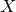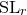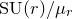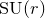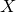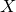1. Introduction
1.1 The
 ${\rm SL}_r$
invariants
${\rm SL}_r$
invariants
Let
![]() $(X,H)$
be a smooth polarized surface over the complex numbers. Suppose
$(X,H)$
be a smooth polarized surface over the complex numbers. Suppose
![]() $H_1(X,\mathbb{Z}) = 0$
and take
$H_1(X,\mathbb{Z}) = 0$
and take
![]() $r \in \mathbb{Z}_{\gt 0}$
,
$r \in \mathbb{Z}_{\gt 0}$
,
![]() $c_1 \in H^2(X,\mathbb{Z})$
,
$c_1 \in H^2(X,\mathbb{Z})$
,
![]() $c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
. We denote by
$c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
. We denote by
![]() $M:=M_X^H(r,c_1,c_2)$
the Gieseker–Maruyama–Simpson moduli space of rank
$M:=M_X^H(r,c_1,c_2)$
the Gieseker–Maruyama–Simpson moduli space of rank
![]() $r$
Gieseker
$r$
Gieseker
![]() $H$
-stable sheaves
$H$
-stable sheaves
![]() $F$
on
$F$
on
![]() $X$
satisfying
$X$
satisfying
![]() $c_1(F) = c_1$
and
$c_1(F) = c_1$
and
![]() $c_2(F) = F$
[HL]. Then
$c_2(F) = F$
[HL]. Then
![]() $M$
is a quasi-projective scheme and it has a natural ‘compactification’ by adding strictly semistable sheaves. Sometimes
$M$
is a quasi-projective scheme and it has a natural ‘compactification’ by adding strictly semistable sheaves. Sometimes
![]() $M$
is itself projective, e.g. when
$M$
is itself projective, e.g. when
![]() $\gcd (r,c_1H)=1$
, in which case Gieseker stability and
$\gcd (r,c_1H)=1$
, in which case Gieseker stability and
![]() $\mu$
-stability coincide, and there are no rank
$\mu$
-stability coincide, and there are no rank
![]() $r$
strictly Gieseker
$r$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with Chern classes
$X$
with Chern classes
![]() $c_1,c_2$
. We view
$c_1,c_2$
. We view
![]() $M$
as a partial compactification of moduli spaces of holomorphic vector bundles, i.e. holomorphic principal
$M$
as a partial compactification of moduli spaces of holomorphic vector bundles, i.e. holomorphic principal
![]() ${\rm GL}_r$
bundles.Footnote
1
${\rm GL}_r$
bundles.Footnote
1
The moduli space
![]() $M$
is virtually smooth; it has a perfect obstruction theory, studied by Mochizuki [Reference MochizukiMoc09], with virtual tangent bundle
$M$
is virtually smooth; it has a perfect obstruction theory, studied by Mochizuki [Reference MochizukiMoc09], with virtual tangent bundle
where
![]() $\pi _M : X \times M \to M$
denotes the projection,
$\pi _M : X \times M \to M$
denotes the projection,
![]() $R \mathcal{H}{\textit{om}}_{\pi _M} = R\pi _{M*} \circ R \mathcal{H}{\textit{om}}$
,
$R \mathcal{H}{\textit{om}}_{\pi _M} = R\pi _{M*} \circ R \mathcal{H}{\textit{om}}$
,
![]() $(\cdot )_0$
denotes trace-free part and
$(\cdot )_0$
denotes trace-free part and
![]() $\mathcal{E}$
is a universal sheaf on
$\mathcal{E}$
is a universal sheaf on
![]() $X \times M$
. In general, a universal sheaf
$X \times M$
. In general, a universal sheaf
![]() $\mathcal{E}$
only exists étale locally on
$\mathcal{E}$
only exists étale locally on
![]() $X \times M$
, but the virtual tangent bundle exists globally by [Reference CăldăraruCal00, Theorem 2.2.4] (see also [Reference Huybrechts and LehnHL10, §10.2]). We assume
$X \times M$
, but the virtual tangent bundle exists globally by [Reference CăldăraruCal00, Theorem 2.2.4] (see also [Reference Huybrechts and LehnHL10, §10.2]). We assume
![]() $\gcd (r,c_1H)=1$
. Then
$\gcd (r,c_1H)=1$
. Then
![]() $M$
is projective and, by work of Behrend and Fantechi [Reference Behrend and FantechiBF97] and Li and Tian [Reference Li and TianLT98], there exists a virtual fundamental class
$M$
is projective and, by work of Behrend and Fantechi [Reference Behrend and FantechiBF97] and Li and Tian [Reference Li and TianLT98], there exists a virtual fundamental class
where
![]() $A_*(M)$
denotes the Chow group of
$A_*(M)$
denotes the Chow group of
![]() $M$
.
$M$
.
Intersection numbers obtained by capping with the virtual fundamental class play a key role in enumerative geometry, gauge theory and physics. Examples of such intersection numbers are virtual Euler characteristics,
![]() $\chi _y$
-genera, elliptic genera, cobordism classes, Donaldson invariants, Segre numbers and Verlinde numbers. In the cases
$\chi _y$
-genera, elliptic genera, cobordism classes, Donaldson invariants, Segre numbers and Verlinde numbers. In the cases
![]() $HK_X \lt 0$
or
$HK_X \lt 0$
or
![]() $K_X \cong \mathcal{O}_X$
,
$K_X \cong \mathcal{O}_X$
,
![]() $M$
is smooth of expected dimension and these numbers have a long history going back (at least) to the 1990s. In this paper, we focus on surfaces with a non-zero holomorphic 2-form, i.e.
$M$
is smooth of expected dimension and these numbers have a long history going back (at least) to the 1990s. In this paper, we focus on surfaces with a non-zero holomorphic 2-form, i.e.
![]() $h^{2,0}(X) \gt 0$
, in which case
$h^{2,0}(X) \gt 0$
, in which case
![]() $M$
is typically singular and may not have expected dimension (see e.g. [Reference Mestrano and SimpsonMS18] for examples). For a (partial) survey on this rich subject, we refer to [Reference Göttsche and KoolGK20a] and references therein. One key feature of these ‘virtual intersection numbers’ is that they are invariant under deformations of
$M$
is typically singular and may not have expected dimension (see e.g. [Reference Mestrano and SimpsonMS18] for examples). For a (partial) survey on this rich subject, we refer to [Reference Göttsche and KoolGK20a] and references therein. One key feature of these ‘virtual intersection numbers’ is that they are invariant under deformations of
![]() $X$
.
$X$
.
Perhaps the most interesting case is the generating function of virtual Euler characteristics
where
![]() $c(\cdot )$
denotes the total Chern class, which plays a central role in Vafa–Witten theory [Reference Tanaka and ThomasTT20]. In the ground-breaking work of Vafa and Witten [Reference Vafa and WittenVW94] on
$c(\cdot )$
denotes the total Chern class, which plays a central role in Vafa–Witten theory [Reference Tanaka and ThomasTT20]. In the ground-breaking work of Vafa and Witten [Reference Vafa and WittenVW94] on
![]() $S$
-duality and
$S$
-duality and
![]() $N=4$
supersymmetric Yang–Mills theory on the 4-manifold underlying
$N=4$
supersymmetric Yang–Mills theory on the 4-manifold underlying
![]() $X$
, such generating functions are predicted to be Fourier expansions of meromorphic functions on the upper half-plane with beautiful modular properties. Notably, under the
$X$
, such generating functions are predicted to be Fourier expansions of meromorphic functions on the upper half-plane with beautiful modular properties. Notably, under the
![]() $S$
-duality transformation, a certain generating function associated with gauge group
$S$
-duality transformation, a certain generating function associated with gauge group
![]() ${\rm SU}(r)$
and its Langlands dual
${\rm SU}(r)$
and its Langlands dual
![]() ${\rm PSU}(r) = {\rm SU}(r) / \mu _r$
are related. We denote by
${\rm PSU}(r) = {\rm SU}(r) / \mu _r$
are related. We denote by
![]() $\mu _r$
the multiplicative cyclic group of order
$\mu _r$
the multiplicative cyclic group of order
![]() $r$
.
$r$
.
In this paper, we consider essentially arbitrary intersection numbers on Gieseker–Maruyama–Simpson moduli spaces obtained as polynomial expressions in ‘descendent insertions’ as defined in §4.2. Besides virtual Euler characteristics this includes, e.g. the Segre and Verlinde numbers studied in [Reference Göttsche and KoolGK22, Reference Göttsche and MellitGM22, Reference Marian, Oprea and PandharipandeMOP22, Reference YuanYua22]. For a choice of formal insertions
![]() $\mathsf{P}$
, we denote the corresponding generating function by
$\mathsf{P}$
, we denote the corresponding generating function by
![]() $\mathsf{Z}^{{\rm SL}_r,\mathsf{P}}_{(X,H),c_1}(q)$
. There are several powerful tools for the calculation of virtual intersection numbers, notably Mochizuki’s formula [Reference MochizukiMoc09] and the new vertex algebra wall-crossing technology developed by Joyce and collaborators [Reference Gross, Joyce and TanakaGJT22, Reference JoyceJoy21].
$\mathsf{Z}^{{\rm SL}_r,\mathsf{P}}_{(X,H),c_1}(q)$
. There are several powerful tools for the calculation of virtual intersection numbers, notably Mochizuki’s formula [Reference MochizukiMoc09] and the new vertex algebra wall-crossing technology developed by Joyce and collaborators [Reference Gross, Joyce and TanakaGJT22, Reference JoyceJoy21].
1.2 The
 ${\rm PGL}_r$
invariants
${\rm PGL}_r$
invariants
In this paper, we are interested in compactifications of moduli spaces of holomorphic
![]() $\mathbb{P}^{r-1}$
-bundles, i.e. holomorphic principal
$\mathbb{P}^{r-1}$
-bundles, i.e. holomorphic principal
![]() ${\rm PGL}_r$
bundles with
${\rm PGL}_r$
bundles with
![]() $r\gt 1$
. The correct approach for dealing with these objects within algebraic geometry is by using moduli spaces of twisted sheaves. Instead of first Chern class
$r\gt 1$
. The correct approach for dealing with these objects within algebraic geometry is by using moduli spaces of twisted sheaves. Instead of first Chern class
![]() $c_1$
, we now fix a Stiefel–Whitney classFootnote
2
$c_1$
, we now fix a Stiefel–Whitney classFootnote
2
![]() $w \in H^2(X,\mu _r)$
, where we view the multiplicative group
$w \in H^2(X,\mu _r)$
, where we view the multiplicative group
![]() $\mu _r$
of
$\mu _r$
of
![]() $r$
th roots of unity as a constructible sheaf on
$r$
th roots of unity as a constructible sheaf on
![]() $X$
in the étale topology. In fact,
$X$
in the étale topology. In fact,
![]() $H^2(X,\mu _r)$
is isomorphic to the singular cohomology group
$H^2(X,\mu _r)$
is isomorphic to the singular cohomology group
![]() $H^2(X,\mathbb{Z} / r\mathbb{Z})$
, where
$H^2(X,\mathbb{Z} / r\mathbb{Z})$
, where
![]() $X$
is endowed with its complex analytic topology [Reference MilneMil13, Theorem 21.1]. The inclusion
$X$
is endowed with its complex analytic topology [Reference MilneMil13, Theorem 21.1]. The inclusion
![]() $\mu _r \leq \mathbb{G}_m$
induces a map
$\mu _r \leq \mathbb{G}_m$
induces a map
where
![]() $H^2(X,\mathbb{G}_m)$
is isomorphic to the Brauer group
$H^2(X,\mathbb{G}_m)$
is isomorphic to the Brauer group
![]() ${\rm Br}(X)$
. For
${\rm Br}(X)$
. For
![]() $\alpha :=o(w)$
, there are many models for twisted sheaves on
$\alpha :=o(w)$
, there are many models for twisted sheaves on
![]() $X$
.
$X$
.
-
• Căldăraru [Reference CăldăraruCal00]. Perhaps the most intuitive approach is to represent
 $\alpha \in H^2(X,\mathbb{G}_m)$
by a Čech 2-cocycle
$\alpha \in H^2(X,\mathbb{G}_m)$
by a Čech 2-cocycle
 $\{\alpha _{ijk} \in H^0(U_{ijk}, \mathbb{G}_m)\}$
, where
$\{\alpha _{ijk} \in H^0(U_{ijk}, \mathbb{G}_m)\}$
, where
 $\{U_i \to X\}$
is an étale cover and we write
$\{U_i \to X\}$
is an étale cover and we write
 $U_{ij} = U_i \times _X U_j$
,
$U_{ij} = U_i \times _X U_j$
,
 $U_{ijk} = U_i \times _X U_j \times _X U_k$
. Then an
$U_{ijk} = U_i \times _X U_j \times _X U_k$
. Then an
 $\alpha$
-twisted sheaf consists of a collection of sheaves
$\alpha$
-twisted sheaf consists of a collection of sheaves
 $\{F_i \in {\rm Coh}(U_i) \}$
together with isomorphism
$\{F_i \in {\rm Coh}(U_i) \}$
together with isomorphism
 $\{\phi : F_i |_{U_{ij}} \to F_j|_{U_{ij}}\}$
satisfying
$\{\phi : F_i |_{U_{ij}} \to F_j|_{U_{ij}}\}$
satisfying
 $\phi _{ii} = {\rm id}$
,
$\phi _{ii} = {\rm id}$
,
 $\phi _{ji} = \phi _{ij}^{-1}$
, and
$\phi _{ji} = \phi _{ij}^{-1}$
, and
 $\phi _{ij} \circ \phi _{jk} \circ \phi _{ki} = \alpha _{ijk} \cdot {\rm id}$
for all
$\phi _{ij} \circ \phi _{jk} \circ \phi _{ki} = \alpha _{ijk} \cdot {\rm id}$
for all
 $i,j,k$
.
$i,j,k$
. -
• Yoshioka [Reference YoshiokaYos06]. Let
 $[\pi : Y \to X] \in H^1(X,{\rm PGL}_r)$
be a degree
$[\pi : Y \to X] \in H^1(X,{\rm PGL}_r)$
be a degree
 $r$
Brauer–Severi variety, i.e. étale
$r$
Brauer–Severi variety, i.e. étale
 $\mathbb{P}^{r-1}$
fibre bundle, with Stiefel–Whitney class
$\mathbb{P}^{r-1}$
fibre bundle, with Stiefel–Whitney class
 $w(Y) = w \in H^2(X,\mu _r)$
. It is a consequence of the period-index theorem, proved by de Jong [Reference de JongdJo04], [Reference LieblichLie08, Corollary 4.2.2.4], that such a Brauer–Severi variety exists. Yoshioka defines the notion of
$w(Y) = w \in H^2(X,\mu _r)$
. It is a consequence of the period-index theorem, proved by de Jong [Reference de JongdJo04], [Reference LieblichLie08, Corollary 4.2.2.4], that such a Brauer–Severi variety exists. Yoshioka defines the notion of
 $Y$
-sheaves. These are essentially pull-backs of
$Y$
-sheaves. These are essentially pull-backs of
 $\alpha$
-twisted sheaves from
$\alpha$
-twisted sheaves from
 $X$
to
$X$
to
 $Y$
tensored with the
$Y$
tensored with the
 $-\pi ^* \alpha$
-twisted line bundle
$-\pi ^* \alpha$
-twisted line bundle
 $\mathcal{O}_Y(1)$
, which removes the twist.
$\mathcal{O}_Y(1)$
, which removes the twist. -
• Lieblich [Reference LieblichLie07]. Let
 $\mathcal{G} \to X$
be the
$\mathcal{G} \to X$
be the
 $\mu _r$
-gerbe associated with
$\mu _r$
-gerbe associated with
 $w \in H^2(X, \mu _r)$
. Then Lieblich introduces twisted sheaves on
$w \in H^2(X, \mu _r)$
. Then Lieblich introduces twisted sheaves on
 $\mathcal{G}$
. Roughly speaking, coherent sheaves on
$\mathcal{G}$
. Roughly speaking, coherent sheaves on
 $\mathcal{G}$
decompose with respect to the character group of
$\mathcal{G}$
decompose with respect to the character group of
 $\mu _r$
and the twisted sheaves are the weight 1 eigensheaves.
$\mu _r$
and the twisted sheaves are the weight 1 eigensheaves. -
• Hoffmann and Stuhler [Reference Hoffmann and StuhlerHS05]. One can also view elements of
 $H^1(X,{\rm PGL}_r)$
as isomorphism classes of degree
$H^1(X,{\rm PGL}_r)$
as isomorphism classes of degree
 $r$
Azumaya algebras on
$r$
Azumaya algebras on
 $X$
. Indeed, there exists a non-trivial extension
$X$
. Indeed, there exists a non-trivial extension
 $0 \to \mathcal{O}_Y \to G \to T_{Y/X} \to 0$
(unique up to scaling), where
$0 \to \mathcal{O}_Y \to G \to T_{Y/X} \to 0$
(unique up to scaling), where
 $T_{Y/X}$
denotes the relative tangent bundle. Then
$T_{Y/X}$
denotes the relative tangent bundle. Then
 $\mathcal{A} = \pi _*(\mathcal{E}{\textit{nd}}(G^\vee ))$
is the degree
$\mathcal{A} = \pi _*(\mathcal{E}{\textit{nd}}(G^\vee ))$
is the degree
 $r$
Azumaya algebra corresponding to
$r$
Azumaya algebra corresponding to
 $Y$
(Lemma 2.4, Proposition 2.5). Suppose
$Y$
(Lemma 2.4, Proposition 2.5). Suppose
 $\mathcal{A}$
has Stiefel–Whitney class
$\mathcal{A}$
has Stiefel–Whitney class
 $w \in H^2(X,\mu _r)$
. Then Hoffmann–Stuhler introduce moduli spaces of (left)
$w \in H^2(X,\mu _r)$
. Then Hoffmann–Stuhler introduce moduli spaces of (left)
 $\mathcal{A}$
-modules which are generically simple. These modules provide another model for twisted sheaves. Azumaya algebras are generalizations of central simple algebras, which in turn are generalizations of division algebras. The latter have a long history dating back to Hamilton.
$\mathcal{A}$
-modules which are generically simple. These modules provide another model for twisted sheaves. Azumaya algebras are generalizations of central simple algebras, which in turn are generalizations of division algebras. The latter have a long history dating back to Hamilton.
We survey these models for twisted sheaves and their equivalences in §2. We will mostly work with the moduli spaces of Yoshioka and Hoffmann–Stuhler, and occasionally the one of Lieblich (§3.2).
Let
![]() $Y \to X$
be a degree
$Y \to X$
be a degree
![]() $r$
Brauer–Severi variety with Stiefel–Whitney class
$r$
Brauer–Severi variety with Stiefel–Whitney class
![]() $w:=w(Y) \in H^2(X,\mu _r)$
. Then we consider the generating function of virtual Euler characteristicsFootnote
3
$w:=w(Y) \in H^2(X,\mu _r)$
. Then we consider the generating function of virtual Euler characteristicsFootnote
3
where we assume all of the moduli spaces of
![]() $H$
-stable
$H$
-stable
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $M_Y^H(r,0,c_2)$
(which we recall in §3) are projective. For instance, this is the case when the Brauer class
$M_Y^H(r,0,c_2)$
(which we recall in §3) are projective. For instance, this is the case when the Brauer class
![]() $o(w) \in H^2(X,\mathbb{G}_m)$
has order
$o(w) \in H^2(X,\mathbb{G}_m)$
has order
![]() $r$
. Indeed, then there are no
$r$
. Indeed, then there are no
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $F$
of rank
$F$
of rank
![]() $0 \lt{{\rm rk}}(F) \lt r$
, thus stability is automatic and there are no rank
$0 \lt{{\rm rk}}(F) \lt r$
, thus stability is automatic and there are no rank
![]() $r$
strictly semistable
$r$
strictly semistable
![]() $Y$
-sheaves (Remark 3.5). In this case, the generating function does not depend on the choice of polarization
$Y$
-sheaves (Remark 3.5). In this case, the generating function does not depend on the choice of polarization
![]() $H$
and we write
$H$
and we write
We show in Proposition 4.9 that the generating function does not depend on the choice of degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
.
$Y \to X$
.
As in the
![]() ${\rm SL}_r$
case, we also consider arbitrary polynomial expressions in descendent insertions on moduli of twisted sheaves. For any choice of formal insertions
${\rm SL}_r$
case, we also consider arbitrary polynomial expressions in descendent insertions on moduli of twisted sheaves. For any choice of formal insertions
![]() $\mathsf{P}$
, we denote the corresponding generating function by
$\mathsf{P}$
, we denote the corresponding generating function by
![]() $\mathsf{Z}^{{\rm PGL}_r,\mathsf{P}}_{(X,H),w}(q)$
(see §4.2 for the precise definition).
$\mathsf{Z}^{{\rm PGL}_r,\mathsf{P}}_{(X,H),w}(q)$
(see §4.2 for the precise definition).
The third-named author first introduced the use of twisted sheaves to Vafa–Witten theory in [Reference JiangJia22]. This was used by the third- and fourth-named authors in [Reference Jiang and KoolJK21] to introduce the
![]() ${\rm PSU}(r)$
Vafa–Witten partition function when
${\rm PSU}(r)$
Vafa–Witten partition function when
![]() $r$
is prime. Denoting
$r$
is prime. Denoting
![]() $\epsilon _r := \exp (2\pi \sqrt{-1} / r)$
, it has the following form:
$\epsilon _r := \exp (2\pi \sqrt{-1} / r)$
, it has the following form:
 \begin{align}\begin{split} & \mathsf{VW}^{{\rm PSU}(r)}_{X,c_1}(q) = \sum _{w \in H^2(X,\mu _r)} \epsilon _r^{c_1 w} \, \mathsf{VW}_{X,w}(q), \\[4pt] & \textrm{where} \quad \mathsf{VW}_{X,w}(q) = \mathsf{Z}^{{\rm PGL}_r,\mathsf{Eu}}_{X,w}(q), \quad if\ 0 \neq o(w) \in {\rm Br}(X). \end{split}\end{align}
\begin{align}\begin{split} & \mathsf{VW}^{{\rm PSU}(r)}_{X,c_1}(q) = \sum _{w \in H^2(X,\mu _r)} \epsilon _r^{c_1 w} \, \mathsf{VW}_{X,w}(q), \\[4pt] & \textrm{where} \quad \mathsf{VW}_{X,w}(q) = \mathsf{Z}^{{\rm PGL}_r,\mathsf{Eu}}_{X,w}(q), \quad if\ 0 \neq o(w) \in {\rm Br}(X). \end{split}\end{align}
1.3 Main results
The construction of the
![]() ${\rm PGL}_r$
generating function on
${\rm PGL}_r$
generating function on
![]() $X$
depends on a choice of a degree
$X$
depends on a choice of a degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
with
$Y \to X$
with
![]() $w(Y)=w$
. Since
$w(Y)=w$
. Since
![]() $Y$
may be obstructed when deforming
$Y$
may be obstructed when deforming
![]() $X$
, deformation invariance of the generating function is not immediate. However, by a result of de Jong [Reference de JongdJo04], when
$X$
, deformation invariance of the generating function is not immediate. However, by a result of de Jong [Reference de JongdJo04], when
![]() $Y$
is obstructed one can always apply an elementary transformation after which it becomes unobstructed. We recall this result in Theorem 4.12. This will lead to the deformation invariance, which we will now describe.
$Y$
is obstructed one can always apply an elementary transformation after which it becomes unobstructed. We recall this result in Theorem 4.12. This will lead to the deformation invariance, which we will now describe.
Let
![]() $f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
$f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
![]() $B$
. Suppose that one fibre (and hence all fibres)
$B$
. Suppose that one fibre (and hence all fibres)
![]() $\mathcal{X}_b$
satisfies
$\mathcal{X}_b$
satisfies
![]() $H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. We fix a family of polarizations
$H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. We fix a family of polarizations
![]() $\mathcal{H}$
on
$\mathcal{H}$
on
![]() $\mathcal{X}$
and we consider
$\mathcal{X}$
and we consider
![]() $\mu _r$
as a constructible sheaf in the étale topology on
$\mu _r$
as a constructible sheaf in the étale topology on
![]() $\mathcal{X}$
. Then
$\mathcal{X}$
. Then
![]() $R^2 f_* \mu _r$
is a constructible sheaf and
$R^2 f_* \mu _r$
is a constructible sheaf and
for all closed points
![]() $b \in B$
by the proper base change theorem [Reference MilneMil13, Theorem 17.7]. We fix a section
$b \in B$
by the proper base change theorem [Reference MilneMil13, Theorem 17.7]. We fix a section
In this paper, we only want to consider the case where there are no strictly semistable objects anywhere in our family. This can be achieved by the following two assumptions:
-
•
 $r$
is prime; and
$r$
is prime; and -
•
 $\gcd (r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
$\gcd (r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
 $b \in B$
.
$b \in B$
.
Since
![]() $r$
is prime and
$r$
is prime and
![]() $\widetilde{w}_b \in H^2(\mathcal{X}_b,\mu _r)$
for any closed point
$\widetilde{w}_b \in H^2(\mathcal{X}_b,\mu _r)$
for any closed point
![]() $b \in B$
, the order of
$b \in B$
, the order of
![]() $o(\widetilde{w}_b) \in H^2(\mathcal{X}_b,\mathbb{G}_m)$
is either 1 or
$o(\widetilde{w}_b) \in H^2(\mathcal{X}_b,\mathbb{G}_m)$
is either 1 or
![]() $r$
. Then for any degree
$r$
. Then for any degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y$
over
$Y$
over
![]() $\mathcal{X}_b$
and any
$\mathcal{X}_b$
and any
![]() $c_2$
, the moduli space
$c_2$
, the moduli space
![]() $M_Y^{\mathcal{H}_b}(r,0,c_2)$
is projective (Lemma 4.11). Roughly speaking, in the case of trivial Brauer class, we are in the untwisted setting and the second condition rules out strictly semistable objects (Proposition 4.10), whereas in the case of non-trivial Brauer class, stability is automatic for all rank
$M_Y^{\mathcal{H}_b}(r,0,c_2)$
is projective (Lemma 4.11). Roughly speaking, in the case of trivial Brauer class, we are in the untwisted setting and the second condition rules out strictly semistable objects (Proposition 4.10), whereas in the case of non-trivial Brauer class, stability is automatic for all rank
![]() $r$
torsion free twisted sheaves, so in particular there are no strictly semistables (Remark 3.5). In order to deal with strictly semistable objects, one should work with a notion of twisted Joyce–Song–Mochizuki pairs [Reference JoyceJoy21, Reference Joyce and SongJS12, Reference MochizukiMoc09].
$r$
torsion free twisted sheaves, so in particular there are no strictly semistables (Remark 3.5). In order to deal with strictly semistable objects, one should work with a notion of twisted Joyce–Song–Mochizuki pairs [Reference JoyceJoy21, Reference Joyce and SongJS12, Reference MochizukiMoc09].
Theorem 1.1.
Let
![]() $\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
$\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
![]() $r$
is prime and
$r$
is prime and
![]() ${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. Then
$b \in B$
. Then
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of the closed point
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of the closed point
![]() $b \in B$
.
$b \in B$
.
This leads us to the following
![]() ${\rm SL}_r$
–
${\rm SL}_r$
–
![]() ${\rm PGL}_r$
correspondence.
${\rm PGL}_r$
correspondence.
Theorem 1.2.
Let
![]() $\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
$\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
![]() $r$
is prime and
$r$
is prime and
![]() ${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. Suppose for some closed point
$b \in B$
. Suppose for some closed point
![]() $0 \in B$
, there exists a class
$0 \in B$
, there exists a class
![]() $\beta \in H^{1,1}(\mathcal{X}_0)$
such that the following composition is surjective:
$\beta \in H^{1,1}(\mathcal{X}_0)$
such that the following composition is surjective:
where the first arrow is the Kodaira–Spencer map and the second is cupping with
![]() $\beta$
followed by contraction. Then any complex analytic simply connected neighbourhood
$\beta$
followed by contraction. Then any complex analytic simply connected neighbourhood
![]() $U$
of
$U$
of
![]() $0$
contains a closed point
$0$
contains a closed point
![]() $b \in U$
such that
$b \in U$
such that
![]() $\widetilde{w}_{b} \in H^2(\mathcal{X}_{b},\mu _r)$
has trivial Brauer class and
$\widetilde{w}_{b} \in H^2(\mathcal{X}_{b},\mu _r)$
has trivial Brauer class and
where
![]() $c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
is any (necessarily algebraic) representative of
$c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
is any (necessarily algebraic) representative of
![]() $\widetilde{w}_{b}$
.
$\widetilde{w}_{b}$
.
The condition of the theorem is mild; it says that there exists at least one
![]() $\beta \in H^{1,1}(\mathcal{X}_0)$
for which the Noether–Lefschetz locus is smooth of expected codimension [Reference Voisin, Farkas and MorrisonVoi13]. The same assumption is used by Green to show that the Hodge locus is dense [Reference VoisinVoi03]. When
$\beta \in H^{1,1}(\mathcal{X}_0)$
for which the Noether–Lefschetz locus is smooth of expected codimension [Reference Voisin, Farkas and MorrisonVoi13]. The same assumption is used by Green to show that the Hodge locus is dense [Reference VoisinVoi03]. When
![]() $\beta$
is an effective algebraic class, this condition appears in the work of Thomas and the fourth-named author on reduced Gromov–Witten/stable pairs theory, and the enumerative geometry of curves in the linear system
$\beta$
is an effective algebraic class, this condition appears in the work of Thomas and the fourth-named author on reduced Gromov–Witten/stable pairs theory, and the enumerative geometry of curves in the linear system
![]() $|\beta |$
[Reference Kool and ThomasKT14a, Reference Kool and ThomasKT14b].
$|\beta |$
[Reference Kool and ThomasKT14a, Reference Kool and ThomasKT14b].
We discuss examples for which the condition of the theorem is satisfied in § 5.1. For example, when
![]() $X \subset \mathbb{P}^3$
is a smooth surface of degree
$X \subset \mathbb{P}^3$
is a smooth surface of degree
![]() $d \geq 4$
, we consider
$d \geq 4$
, we consider
the smooth family of smooth degree
![]() $d$
surfaces. Then the locus of points
$d$
surfaces. Then the locus of points
![]() $b \in B$
for which there exists a
$b \in B$
for which there exists a
![]() $\beta$
satisfying the condition of Theorem 1.2 is dense by a result of Kim [Reference KimKim91]. Hence, we can first use Theorem 1.1 to deform to a point in
$\beta$
satisfying the condition of Theorem 1.2 is dense by a result of Kim [Reference KimKim91]. Hence, we can first use Theorem 1.1 to deform to a point in
![]() $B$
where the condition of Theorem 1.2 is satisfied, and then apply Theorem 1.2 to express the
$B$
where the condition of Theorem 1.2 is satisfied, and then apply Theorem 1.2 to express the
![]() ${\rm PGL}_r$
generating function for
${\rm PGL}_r$
generating function for
![]() $X$
in terms of the
$X$
in terms of the
![]() ${\rm SL}_r$
generating function.
${\rm SL}_r$
generating function.
When
![]() $o(\widetilde{w}_0) \in {\rm Br}(\mathcal{X}_0)$
has order
$o(\widetilde{w}_0) \in {\rm Br}(\mathcal{X}_0)$
has order
![]() $r$
(so in particular
$r$
(so in particular
![]() $h^{2,0}(\mathcal{X}_0) \gt 0$
), we note that
$h^{2,0}(\mathcal{X}_0) \gt 0$
), we note that
![]() $\mathsf{Z}_{(\mathcal{X}_{0},\mathcal{H}_{0}),\widetilde{w}_{0}}^{{\rm PGL}_r, \mathsf{P}}(q) = \mathsf{Z}_{\mathcal{X}_{0},\widetilde{w}_{0}}^{{\rm PGL}_r, \mathsf{P}}(q)$
does not depend on the polarization. In particular, it follows that
$\mathsf{Z}_{(\mathcal{X}_{0},\mathcal{H}_{0}),\widetilde{w}_{0}}^{{\rm PGL}_r, \mathsf{P}}(q) = \mathsf{Z}_{\mathcal{X}_{0},\widetilde{w}_{0}}^{{\rm PGL}_r, \mathsf{P}}(q)$
does not depend on the polarization. In particular, it follows that
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),c_1}^{{\rm SL}_r, \mathsf{P}}(q)$
does not depend on the polarization. It also follows that
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),c_1}^{{\rm SL}_r, \mathsf{P}}(q)$
does not depend on the polarization. It also follows that
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),c_1}^{{\rm SL}_r, \mathsf{P}}(q)$
only depends on
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),c_1}^{{\rm SL}_r, \mathsf{P}}(q)$
only depends on
![]() $c_1 \mod r H^2(\mathcal{X}_b,\mathbb{Z})$
.
$c_1 \mod r H^2(\mathcal{X}_b,\mathbb{Z})$
.
Theorem 1.2 can be viewed as some kind of virtual
![]() ${\rm PGL}_r$
–
${\rm PGL}_r$
–
![]() ${\rm SL}_r$
correspondence. For the comparison of the cohomology of the analogues of our moduli spaces on a smooth projective curve
${\rm SL}_r$
correspondence. For the comparison of the cohomology of the analogues of our moduli spaces on a smooth projective curve
![]() $C$
, we refer to the work of Harder and Narasimhan [Reference Harder and NarasimhanHN75]. Note, however, that
$C$
, we refer to the work of Harder and Narasimhan [Reference Harder and NarasimhanHN75]. Note, however, that
![]() ${\rm Br}(C)=0$
, so the complication is rather in dealing with torsion in
${\rm Br}(C)=0$
, so the complication is rather in dealing with torsion in
![]() ${\rm Pic}(C)$
, which leads to questions of a different flavour. Note that we assume
${\rm Pic}(C)$
, which leads to questions of a different flavour. Note that we assume
![]() $H_1(X,\mathbb{Z}) = 0$
so
$H_1(X,\mathbb{Z}) = 0$
so
![]() ${\rm Pic}(X)$
is torsion free. It will be interesting to study analogues of Theorem 1.2 when
${\rm Pic}(X)$
is torsion free. It will be interesting to study analogues of Theorem 1.2 when
![]() $H_1(X,\mathbb{Z}) \neq 0$
. See [Reference NesterovNes23] for work in this direction when
$H_1(X,\mathbb{Z}) \neq 0$
. See [Reference NesterovNes23] for work in this direction when
![]() $X$
is the product of two curves. In the curve case, upgrade to Higgs moduli spaces is an active research area [Reference Groechenig, Wyss and ZieglerGWZ20, Reference Hausel and ThaddeusHT03, Reference Hoskins and LehalleurHL22, Reference Mestrano and SimpsonMS18]. In the surface case, upgrade to Higgs moduli spaces is the content of the
$X$
is the product of two curves. In the curve case, upgrade to Higgs moduli spaces is an active research area [Reference Groechenig, Wyss and ZieglerGWZ20, Reference Hausel and ThaddeusHT03, Reference Hoskins and LehalleurHL22, Reference Mestrano and SimpsonMS18]. In the surface case, upgrade to Higgs moduli spaces is the content of the
![]() $S$
-duality conjecture.
$S$
-duality conjecture.
The intuitive idea behind the
![]() ${{\rm PGL}}_r$
–
${{\rm PGL}}_r$
–
![]() ${{\rm SL}}_r$
correspondence of Theorem 1.2 is as follows.Footnote
4
We start with a holomorphic
${{\rm SL}}_r$
correspondence of Theorem 1.2 is as follows.Footnote
4
We start with a holomorphic
![]() ${{\rm PGL}}_r$
-bundle
${{\rm PGL}}_r$
-bundle
![]() $Y$
on
$Y$
on
![]() $X$
with Stiefel–Whitney class
$X$
with Stiefel–Whitney class
![]() $w$
. By our assumption
$w$
. By our assumption
![]() $H^3(X,\mathbb{Z}) = 0$
, it is of the form
$H^3(X,\mathbb{Z}) = 0$
, it is of the form
![]() $\mathbb{P}(E)$
for a
$\mathbb{P}(E)$
for a
![]() $C^\infty$
$C^\infty$
![]() ${{\rm GL}}_r$
-bundle
${{\rm GL}}_r$
-bundle
![]() $E$
on
$E$
on
![]() $X$
with first Chern class
$X$
with first Chern class
![]() $\xi$
which is possibly not of Hodge type
$\xi$
which is possibly not of Hodge type
![]() $(1,1)$
. However, by the Hodge theoretic result in Proposition 5.3 (which involves adding large
$(1,1)$
. However, by the Hodge theoretic result in Proposition 5.3 (which involves adding large
![]() $r$
-multiples to
$r$
-multiples to
![]() $\xi$
), we show that, under our assumption on the Noether–Lefschetz locus and after a small change of complex structure of
$\xi$
), we show that, under our assumption on the Noether–Lefschetz locus and after a small change of complex structure of
![]() $X$
, one can arrange
$X$
, one can arrange
![]() $E$
to be holomorphic and
$E$
to be holomorphic and
![]() $\xi$
to be
$\xi$
to be
![]() $(1,1)$
. Therefore, if the original
$(1,1)$
. Therefore, if the original
![]() ${{\rm PGL}}_r$
-bundle
${{\rm PGL}}_r$
-bundle
![]() $Y$
was unobstructed, which can be arranged by de Jong’s result (Theorem 4.12), then
$Y$
was unobstructed, which can be arranged by de Jong’s result (Theorem 4.12), then
![]() $Y = \mathbb{P}(E)$
with
$Y = \mathbb{P}(E)$
with
![]() $E$
a holomorphic
$E$
a holomorphic
![]() ${{\rm GL}}_r$
-bundle in the new complex structure, and this
${{\rm GL}}_r$
-bundle in the new complex structure, and this
![]() $E$
is unique after fixing its determinant. Instead, we first completely settle the deformation invariance question in Theorem 1.1 in the algebro-geometric category, and then use the (complex analytic) Hodge theory result in Proposition 5.3 to find a complex structure where the
$E$
is unique after fixing its determinant. Instead, we first completely settle the deformation invariance question in Theorem 1.1 in the algebro-geometric category, and then use the (complex analytic) Hodge theory result in Proposition 5.3 to find a complex structure where the
![]() ${{\rm PGL}}_r$
count becomes an
${{\rm PGL}}_r$
count becomes an
![]() ${{\rm SL}}_r$
count.
${{\rm SL}}_r$
count.
1.4 Consequences
1.4.1 Application to Vafa–Witten theory
In [Reference Göttsche, Kool and LaarakkerGKL24, Conjecture 1.10], the fourth-named author and Göttsche–Laarakker conjecture a structure formula for the
![]() ${\rm SL}_r$
generating function of virtual Euler characteristics (Conjecture 5.5). It appears this conjecture will be proved in a forthcoming work of Joyce as an application of his vertex algebra wall-crossing formula [Reference JoyceJoy21]. Combined with Theorem 1.2, it leads to a structure formula for the
${\rm SL}_r$
generating function of virtual Euler characteristics (Conjecture 5.5). It appears this conjecture will be proved in a forthcoming work of Joyce as an application of his vertex algebra wall-crossing formula [Reference JoyceJoy21]. Combined with Theorem 1.2, it leads to a structure formula for the
![]() ${\rm PGL}_r$
generating function of virtual Euler characteristics as we now describe. Consider the normalized discriminant modular form
${\rm PGL}_r$
generating function of virtual Euler characteristics as we now describe. Consider the normalized discriminant modular form
 \begin{align*} \overline{\Delta }(q) = \prod _{n=1}^{\infty } (1-q^n)^{24}. \end{align*}
\begin{align*} \overline{\Delta }(q) = \prod _{n=1}^{\infty } (1-q^n)^{24}. \end{align*}
Denote by
![]() $\epsilon _r = \exp (2 \pi \sqrt{-1}/r)$
a primitive
$\epsilon _r = \exp (2 \pi \sqrt{-1}/r)$
a primitive
![]() $r$
th root of unity.
$r$
th root of unity.
Let
![]() $X$
be a smooth projective surface satisfying
$X$
be a smooth projective surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
and
$H_1(X,\mathbb{Z}) = 0$
and
![]() $h^{2,0}(X)\gt 0$
. For an algebraic class
$h^{2,0}(X)\gt 0$
. For an algebraic class
![]() $a \in H^2(X,\mathbb{Z})$
, the linear system
$a \in H^2(X,\mathbb{Z})$
, the linear system
![]() $|a|$
has a perfect obstruction theory and virtual class
$|a|$
has a perfect obstruction theory and virtual class
![]() $|a|^{{\rm vir}}$
in degree
$|a|^{{\rm vir}}$
in degree
![]() $a(a-K_X) / 2$
. If
$a(a-K_X) / 2$
. If
![]() $|a|^{{\rm vir}} \neq 0$
, then
$|a|^{{\rm vir}} \neq 0$
, then
![]() $a^2 = a K_X$
and
$a^2 = a K_X$
and
![]() ${\rm SW}(a) := \deg (|a|^{{\rm vir}})$
[Reference MochizukiMoc09, Proposition 6.3.1]. This is the algebro-geometric definition of Seiberg–Witten invariants of
${\rm SW}(a) := \deg (|a|^{{\rm vir}})$
[Reference MochizukiMoc09, Proposition 6.3.1]. This is the algebro-geometric definition of Seiberg–Witten invariants of
![]() $X$
. A class
$X$
. A class
![]() $a \in H^2(X,\mathbb{Z})$
is called a Seiberg–Witten basic class when
$a \in H^2(X,\mathbb{Z})$
is called a Seiberg–Witten basic class when
![]() ${\rm SW}(a) \neq 0$
.
${\rm SW}(a) \neq 0$
.
Corollary 1.3.
For any prime rank
![]() $r\gt 1$
, there exist
Footnote
5
$r\gt 1$
, there exist
Footnote
5
with the following property. Suppose
![]() $X = \mathcal{X}_0$
and
$X = \mathcal{X}_0$
and
![]() $w = \widetilde{w}_0$
for a family
$w = \widetilde{w}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2 and
$\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2 and
![]() $h^{2,0}(X)\gt 0$
. Fix any
$h^{2,0}(X)\gt 0$
. Fix any
![]() $\delta \in \mathbb{Z}$
such that
$\delta \in \mathbb{Z}$
such that
![]() $\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.5 implies that the coefficient of
$\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.5 implies that the coefficient of
![]() $q^{\delta /2r}$
in
$q^{\delta /2r}$
in
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
equals the coefficient of
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
equals the coefficient of
![]() $q^{\delta /2r}$
in
$q^{\delta /2r}$
in
 \begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i w} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
\begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i w} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
Suppose, in this corollary,
![]() $X$
is moreover minimal of general type. Then its only Seiberg–Witten basic classes are
$X$
is moreover minimal of general type. Then its only Seiberg–Witten basic classes are
![]() $0, K_X$
with Seiberg–Witten invariants
$0, K_X$
with Seiberg–Witten invariants
![]() $1,(-1)^{\chi (\mathcal{O}_X)}$
[Reference MorganMor96, Theorem 7.4.1]. Therefore
$1,(-1)^{\chi (\mathcal{O}_X)}$
[Reference MorganMor96, Theorem 7.4.1]. Therefore
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
only depends on
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
only depends on
The novel feature of this corollary is that it provides an interpretation of the formulae in [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b, Reference Göttsche, Kool and LaarakkerGKL24] in the case
![]() $w$
has non-trivial Brauer class, i.e. it cannot be represented by an algebraic class. By equation (1), this essentially determines the structure of the
$w$
has non-trivial Brauer class, i.e. it cannot be represented by an algebraic class. By equation (1), this essentially determines the structure of the
![]() ${\rm PSU}(r)$
Vafa–Witten partition function of
${\rm PSU}(r)$
Vafa–Witten partition function of
![]() $X$
for prime rank
$X$
for prime rank
![]() $r$
and
$r$
and
![]() $w \in H^2(X,\mu _r)$
with non-trivial Brauer class. This reduces Vafa–Witten’s enigmatic
$w \in H^2(X,\mu _r)$
with non-trivial Brauer class. This reduces Vafa–Witten’s enigmatic
![]() $S$
-duality conjecture (mathematically formulated in [Reference Jiang and KoolJK21]) to a conjecture on the
$S$
-duality conjecture (mathematically formulated in [Reference Jiang and KoolJK21]) to a conjecture on the
![]() ${\rm SU}(r)$
side.
${\rm SU}(r)$
side.
1.4.2 Application to
 $c_2^{{\rm min}}$
of Azumaya algebras
$c_2^{{\rm min}}$
of Azumaya algebras
Let
![]() $X$
be a smooth projective surface with
$X$
be a smooth projective surface with
![]() $H_1(X,\mathbb{Z}) = 0$
and function field
$H_1(X,\mathbb{Z}) = 0$
and function field
![]() $\mathbb{C}(X)$
. Let
$\mathbb{C}(X)$
. Let
![]() $D$
be a (central) division algebra over
$D$
be a (central) division algebra over
![]() $\mathbb{C}(X)$
of degree
$\mathbb{C}(X)$
of degree
![]() $r \gt 1$
(equivalently, an element of
$r \gt 1$
(equivalently, an element of
![]() ${\rm Br}(\mathbb{C}(X))$
of order
${\rm Br}(\mathbb{C}(X))$
of order
![]() $r$
). We assume
$r$
). We assume
![]() $D$
lies in the image of the inclusion
$D$
lies in the image of the inclusion
![]() ${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
(basic facts on the Brauer group are reviewed in § 2.3, see also [Reference SaltmanSal99]).
${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
(basic facts on the Brauer group are reviewed in § 2.3, see also [Reference SaltmanSal99]).
Artin and de Jong [Reference Artin and de JongAdJ04] introduce the
![]() $\mathbb{C}$
-stack
$\mathbb{C}$
-stack
![]() $\mathfrak{A}_{c_2}$
, whose groupoid over a scheme
$\mathfrak{A}_{c_2}$
, whose groupoid over a scheme
![]() $B$
consists of Azumaya algebras
$B$
consists of Azumaya algebras
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X \times B$
such that for all closed points
$X \times B$
such that for all closed points
![]() $b \in B$
, the stalk of
$b \in B$
, the stalk of
![]() $\mathcal{A}|_b$
over the generic point of
$\mathcal{A}|_b$
over the generic point of
![]() $X$
is isomorphic to
$X$
is isomorphic to
![]() $D$
and
$D$
and
![]() $c_2(\mathcal{A}|_b) = c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
. This stack is algebraic and of finite type. Its coarse moduli space
$c_2(\mathcal{A}|_b) = c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
. This stack is algebraic and of finite type. Its coarse moduli space
![]() $\overline{\mathfrak{A}}_{c_2}$
is an algebraic space of finite type [Reference Artin and de JongAdJ04, Theorem 8.7.6]. If
$\overline{\mathfrak{A}}_{c_2}$
is an algebraic space of finite type [Reference Artin and de JongAdJ04, Theorem 8.7.6]. If
![]() $\mathfrak{A}_{c_2}$
is non-empty (i.e. has a
$\mathfrak{A}_{c_2}$
is non-empty (i.e. has a
![]() $\mathbb{C}$
-valued point), then
$\mathbb{C}$
-valued point), then
![]() $c_2 \geq 0$
[Reference Artin and de JongAdJ04, Theorem 7.2.1]. It interesting to consider the minimal value
$c_2 \geq 0$
[Reference Artin and de JongAdJ04, Theorem 7.2.1]. It interesting to consider the minimal value
![]() $c_2 = c_2^{{\rm min}}$
for which
$c_2 = c_2^{{\rm min}}$
for which
![]() $\mathfrak{A}_{c_2}$
is non-empty, because
$\mathfrak{A}_{c_2}$
is non-empty, because
![]() $\mathfrak{A}_{c_2^{{\rm min}}}$
,
$\mathfrak{A}_{c_2^{{\rm min}}}$
,
![]() $\overline{\mathfrak{A}}_{c_2^{{\rm min}}}$
are proper [Reference Artin and de JongAdJ04, Theorem 8.7.7]. Artin and de Jong proved that [Reference Artin and de JongAdJ04, Corollary 7.1.5, Theorem 7.2.1]
$\overline{\mathfrak{A}}_{c_2^{{\rm min}}}$
are proper [Reference Artin and de JongAdJ04, Theorem 8.7.7]. Artin and de Jong proved that [Reference Artin and de JongAdJ04, Corollary 7.1.5, Theorem 7.2.1]
We show the following.
Theorem 1.4.
Suppose
![]() $X = \mathcal{X}_0$
for a family
$X = \mathcal{X}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2
, and
$\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2
, and
![]() $X$
is a minimal surface of general type satisfying
$X$
is a minimal surface of general type satisfying
![]() $h^{2,0}(X)\gt 0$
. Let
$h^{2,0}(X)\gt 0$
. Let
![]() $D \in {\rm Br}(\mathbb{C}(X))$
be a degree
$D \in {\rm Br}(\mathbb{C}(X))$
be a degree
![]() $r$
division algebra in the image of
$r$
division algebra in the image of
![]() ${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. Then, for
${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. Then, for
![]() $r=2$
, we have
$r=2$
, we have
Moreover, for
![]() $r=3$
and assuming Göttsche’s conjecture 5.9 for
$r=3$
and assuming Göttsche’s conjecture 5.9 for
![]() $r=3$
, we have
$r=3$
, we have
For minimal surfaces
![]() $X$
of general type, we have plurigenera
$X$
of general type, we have plurigenera
![]() $h^0(\omega _X^{\otimes r}) = {1 \over 2}r(r-1)K_X^2+\chi (\mathcal{O}_X)$
[Reference BombieriBom72]. For
$h^0(\omega _X^{\otimes r}) = {1 \over 2}r(r-1)K_X^2+\chi (\mathcal{O}_X)$
[Reference BombieriBom72]. For
![]() $r=2$
and
$r=2$
and
![]() $p_g(X) = K_X^2=1$
(which implies
$p_g(X) = K_X^2=1$
(which implies
![]() $H_1(X,\mathbb{Z}) = 0$
[Reference BombieriBom72]), this leaves very little room:
$H_1(X,\mathbb{Z}) = 0$
[Reference BombieriBom72]), this leaves very little room:
![]() $c_2^{{\rm min}} \in \{4,5,6,7\}$
.
$c_2^{{\rm min}} \in \{4,5,6,7\}$
.
The
![]() $r=2$
case of Theorem 1.4 is proved by combining Theorem 1.2 with Witten’s conjecture and a result of Hoffmann and Stuhler (Proposition 3.8). Witten’s conjecture, proved by Göttsche, Nakajima and Yoshioka [Reference Göttsche, Nakajima and YoshiokaGNY11] in the algebro-geometric set-up, expresses Donaldson invariants in terms of Seiberg–Witten invariants (Theorem 5.8). The
$r=2$
case of Theorem 1.4 is proved by combining Theorem 1.2 with Witten’s conjecture and a result of Hoffmann and Stuhler (Proposition 3.8). Witten’s conjecture, proved by Göttsche, Nakajima and Yoshioka [Reference Göttsche, Nakajima and YoshiokaGNY11] in the algebro-geometric set-up, expresses Donaldson invariants in terms of Seiberg–Witten invariants (Theorem 5.8). The
![]() $r=3$
case follows similarly, but instead using the higher rank generalization of Witten’s conjecture by Mariño and Moore [Reference Mariño and MooreMM98] (see also [Reference Labastida and MariñoLM05]), or rather its explicit form in the algebro-geometric set-up due to Göttsche [Reference GöttscheGot21].
$r=3$
case follows similarly, but instead using the higher rank generalization of Witten’s conjecture by Mariño and Moore [Reference Mariño and MooreMM98] (see also [Reference Labastida and MariñoLM05]), or rather its explicit form in the algebro-geometric set-up due to Göttsche [Reference GöttscheGot21].
This is an illustration of a general strategy described in detail in § 5.3. Suppose
![]() $X = \mathcal{X}_0$
for a family
$X = \mathcal{X}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2.
$\mathcal{X} \to B$
satisfying the conditions of Theorem 1.2.
-
• Show that some virtual intersection number
 $\int _{[M]^{{\rm vir}}} \mathsf{P}$
, for
$\int _{[M]^{{\rm vir}}} \mathsf{P}$
, for
 $M$
some moduli space of twisted sheaves on
$M$
some moduli space of twisted sheaves on
 $X$
of virtual dimension
$X$
of virtual dimension
 $\delta$
, is non-zero.
$\delta$
, is non-zero. -
• Then there exists an Azumaya algebra
 $\mathcal{A}$
on
$\mathcal{A}$
on
 $X$
with
$X$
with
 $\mathcal{A}_{\eta } \cong D$
satisfying
$\mathcal{A}_{\eta } \cong D$
satisfying
 $c_2(\mathcal{A}) \leq \delta + (r^2-1)\chi (\mathcal{O}_X)$
, where
$c_2(\mathcal{A}) \leq \delta + (r^2-1)\chi (\mathcal{O}_X)$
, where
 $\eta$
is the generic point of
$\eta$
is the generic point of
 $X$
.
$X$
.
On the other hand, non-emptiness of
![]() $\mathfrak{A}_{c_2}$
for large
$\mathfrak{A}_{c_2}$
for large
![]() $c_2$
was established by Lieblich (see Remark 3.11).
$c_2$
was established by Lieblich (see Remark 3.11).
Notation and conventions
In this paper,
![]() $X$
always denotes a smooth projective variety over
$X$
always denotes a smooth projective variety over
![]() $\mathbb{C}$
. If
$\mathbb{C}$
. If
![]() $E$
is a locally free sheaf on any scheme, then
$E$
is a locally free sheaf on any scheme, then
![]() $\mathbb{P}(E)$
is defined as
$\mathbb{P}(E)$
is defined as
![]() $\textrm{Proj}\,{{\rm Sym}}^\bullet E$
, which is the moduli space of quotients
$\textrm{Proj}\,{{\rm Sym}}^\bullet E$
, which is the moduli space of quotients
![]() $E \twoheadrightarrow L$
with
$E \twoheadrightarrow L$
with
![]() $L$
an invertible sheaf. In this paper, we will use both singular cohomology, with respect to the complex analytic topology, and étale cohomology. By convention,
$L$
an invertible sheaf. In this paper, we will use both singular cohomology, with respect to the complex analytic topology, and étale cohomology. By convention,
![]() $H^i(X, A)$
will denote singular cohomology when
$H^i(X, A)$
will denote singular cohomology when
![]() $A = \mathbb{Z}$
,
$A = \mathbb{Z}$
,
![]() $\mathbb{Q}$
,
$\mathbb{Q}$
,
![]() $\mathbb{R}$
,
$\mathbb{R}$
,
![]() $\mathbb{C}$
or
$\mathbb{C}$
or
![]() $\mathbb{Z}/r\mathbb{Z}$
. On the other hand, the groups
$\mathbb{Z}/r\mathbb{Z}$
. On the other hand, the groups
![]() $A = \mu _r$
,
$A = \mu _r$
,
![]() $\mathbb{G}_m$
,
$\mathbb{G}_m$
,
![]() ${\rm SL}_r$
,
${\rm SL}_r$
,
![]() ${\rm GL}_r$
,
${\rm GL}_r$
,
![]() ${\rm PGL}_r$
can be viewed as sheaves of groups
${\rm PGL}_r$
can be viewed as sheaves of groups
![]() $\mu _r(\mathcal{O}_X)$
,
$\mu _r(\mathcal{O}_X)$
,
![]() $\mathcal{O}_X^{\times }$
,
$\mathcal{O}_X^{\times }$
,
![]() ${\rm SL}_r(\mathcal{O}_X)$
,
${\rm SL}_r(\mathcal{O}_X)$
,
![]() ${\rm GL}_r(\mathcal{O}_X)$
,
${\rm GL}_r(\mathcal{O}_X)$
,
![]() ${\rm PGL}_r(\mathcal{O}_X)$
in the étale topology and we denote the corresponding étale cohomology groups by
${\rm PGL}_r(\mathcal{O}_X)$
in the étale topology and we denote the corresponding étale cohomology groups by
![]() $H^i(X,A)$
.
$H^i(X,A)$
.
2. Models of twisted sheaves
2.1 Brauer–Severi varieties, Azumaya algebras and gerbes
In this section, we recall the notions of Brauer–Severi variety, Azumaya algebra and gerbe, and gather various known facts about them. Let
![]() $X$
be a smooth projective variety over
$X$
be a smooth projective variety over
![]() $\mathbb{C}$
.
$\mathbb{C}$
.
Definition 2.1. A Brauer–Severi variety of degree
![]() $r$
over
$r$
over
![]() $X$
is a scheme
$X$
is a scheme
![]() $Y \to X$
for which there exists an étale cover
$Y \to X$
for which there exists an étale cover
![]() $\{U_i\}$
of
$\{U_i\}$
of
![]() $X$
on which
$X$
on which
![]() $Y \to X$
is isomorphic to the projection
$Y \to X$
is isomorphic to the projection
![]() $\mathbb{P}^{r-1}_{U_i} := \mathbb{P}^{r-1} \times U_i \to U_i$
. An Azumaya algebra of degree
$\mathbb{P}^{r-1}_{U_i} := \mathbb{P}^{r-1} \times U_i \to U_i$
. An Azumaya algebra of degree
![]() $r$
on
$r$
on
![]() $X$
is a coherent sheaf of
$X$
is a coherent sheaf of
![]() $\mathcal{O}_X$
-algebras
$\mathcal{O}_X$
-algebras
![]() $\mathcal{A}$
for which there exists an étale cover
$\mathcal{A}$
for which there exists an étale cover
![]() $\{U_i\}$
of
$\{U_i\}$
of
![]() $X$
on which
$X$
on which
![]() $\mathcal{A}$
is isomorphic to the matrix algebra
$\mathcal{A}$
is isomorphic to the matrix algebra
![]() $M_r(\mathcal{O}_{U_i})$
.
$M_r(\mathcal{O}_{U_i})$
.
We will recall below that the data of a Brauer–Severi variety over
![]() $X$
is equivalent to the data of an Azumaya algebra on
$X$
is equivalent to the data of an Azumaya algebra on
![]() $X$
. We first recall the following version of the Skolem–Noether theorem [Reference MilneMil80, Proposition IV.2.3].
$X$
. We first recall the following version of the Skolem–Noether theorem [Reference MilneMil80, Proposition IV.2.3].
Theorem 2.2. (Skolem–Noether). For any Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
and any automorphism
$X$
and any automorphism
![]() $\phi \in{{\rm Aut}} (\mathcal{A})$
, there is a covering of
$\phi \in{{\rm Aut}} (\mathcal{A})$
, there is a covering of
![]() $X$
by Zariski open subsets
$X$
by Zariski open subsets
![]() $\{U_i\}$
such that
$\{U_i\}$
such that
![]() $\phi |_{U_i}$
is of the form
$\phi |_{U_i}$
is of the form
![]() $a \mapsto u a u^{-1}$
for some
$a \mapsto u a u^{-1}$
for some
![]() $u \in \Gamma (U_i,\mathcal{A})^{\times }$
for all
$u \in \Gamma (U_i,\mathcal{A})^{\times }$
for all
![]() $i$
.
$i$
.
Corollary 2.3.
We have an isomorphism of sheaves
![]() ${\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X)) \cong{{\rm PGL}}_r$
in the étale topology.
${\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X)) \cong{{\rm PGL}}_r$
in the étale topology.
Proof.
The Skolem–Noether theorem implies that every automorphism of
![]() $M_r(\mathcal{O}_X)$
is locally given by conjugation by an invertible matrix, so that
$M_r(\mathcal{O}_X)$
is locally given by conjugation by an invertible matrix, so that
![]() ${{\rm GL}}_r \to{\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X))$
is a surjection of sheaves. The kernel of this surjection is
${{\rm GL}}_r \to{\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X))$
is a surjection of sheaves. The kernel of this surjection is
![]() $\mathbb{G}_m$
from which the result follows.
$\mathbb{G}_m$
from which the result follows.
The facts in the following lemma are all proved in [Reference YoshiokaYos06, §1.1].
Lemma 2.4.
If
![]() $\pi : Y \to X$
is a Brauer–Severi variety with relative tangent sheaf
$\pi : Y \to X$
is a Brauer–Severi variety with relative tangent sheaf
![]() $T_{Y/X}$
, then there is a unique (up to scaling) sheaf
$T_{Y/X}$
, then there is a unique (up to scaling) sheaf
![]() $G$
fitting in a non-trivial short exact sequence
$G$
fitting in a non-trivial short exact sequence
Furthermore, the sheaf
![]() $G$
satisfies the properties
$G$
satisfies the properties
![]() $R \pi _*(G^\vee ) = 0$
and the canonical map
$R \pi _*(G^\vee ) = 0$
and the canonical map
![]() $\pi ^* \pi _* (\mathcal{E}{\textit{nd}}(G^\vee )) \to \mathcal{E}{\textit{nd}}(G^\vee )$
is an isomorphism, where
$\pi ^* \pi _* (\mathcal{E}{\textit{nd}}(G^\vee )) \to \mathcal{E}{\textit{nd}}(G^\vee )$
is an isomorphism, where
![]() $\mathcal{E}{\textit{nd}}(G^\vee ) := G^\vee \otimes G$
.
$\mathcal{E}{\textit{nd}}(G^\vee ) := G^\vee \otimes G$
.
We now state the following classification result on Brauer–Severi varieties and Azumaya algebras.
Proposition 2.5.
There is a canonical bijection of sets between (isomorphism classes of) Brauer–Severi varieties of degree
![]() $r$
over
$r$
over
![]() $X$
and Azumaya algebras of degree
$X$
and Azumaya algebras of degree
![]() $r$
on
$r$
on
![]() $X$
. Furthermore, both are equivalent to the set of
$X$
. Furthermore, both are equivalent to the set of
![]() ${{\rm PGL}}_r$
-torsors, classified by
${{\rm PGL}}_r$
-torsors, classified by
![]() $H^1(X,{{\rm PGL}}_r)$
.
$H^1(X,{{\rm PGL}}_r)$
.
We only provide a sketch of the proof.
Sketch of proof.
We first describe the bijection, for the details of this part we refer to [Reference ReedeRee18]. If
![]() $\pi : Y \to X$
is a degree
$\pi : Y \to X$
is a degree
![]() $r$
Brauer–Severi variety, then
$r$
Brauer–Severi variety, then
![]() $\pi _*(\mathcal{E}{\textit{nd}}(G^\vee ))$
is a degree
$\pi _*(\mathcal{E}{\textit{nd}}(G^\vee ))$
is a degree
![]() $r$
Azumaya algebra.Footnote
6
Conversely, if
$r$
Azumaya algebra.Footnote
6
Conversely, if
![]() $\mathcal{A}$
is a degree
$\mathcal{A}$
is a degree
![]() $r$
Azumaya algebra on
$r$
Azumaya algebra on
![]() $X$
, we can consider the moduli space of left ideals
$X$
, we can consider the moduli space of left ideals
![]() $I \subseteq \mathcal{A}$
such that
$I \subseteq \mathcal{A}$
such that
![]() $\mathcal{A}/I$
is a locally free
$\mathcal{A}/I$
is a locally free
![]() $\mathcal{O}_X$
-module of rank
$\mathcal{O}_X$
-module of rank
![]() $r(r - 1)$
, which is a degree
$r(r - 1)$
, which is a degree
![]() $r$
Brauer–Severi variety over
$r$
Brauer–Severi variety over
![]() $X$
.
$X$
.
For a degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
, we consider the sheaf
$Y \to X$
, we consider the sheaf
![]() $\mathcal{I}{\textit{som}}(Y, \mathbb{P}^{r-1}_X)$
of isomorphisms of schemes over
$\mathcal{I}{\textit{som}}(Y, \mathbb{P}^{r-1}_X)$
of isomorphisms of schemes over
![]() $X$
. This sheaf admits an action of
$X$
. This sheaf admits an action of
![]() ${\mathcal{A}\textit{ut}}(\mathbb{P}^{r-1}_X) \cong{{\rm PGL}}_r$
,Footnote
7
and locally, where
${\mathcal{A}\textit{ut}}(\mathbb{P}^{r-1}_X) \cong{{\rm PGL}}_r$
,Footnote
7
and locally, where
![]() $Y$
is trivial, this action is free and transitive. Therefore, this is a
$Y$
is trivial, this action is free and transitive. Therefore, this is a
![]() ${{\rm PGL}}_r$
-torsor. Similarly, for a degree
${{\rm PGL}}_r$
-torsor. Similarly, for a degree
![]() $r$
Azumaya algebra
$r$
Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
, one can consider the sheaf
$X$
, one can consider the sheaf
![]() $\mathcal{I}{\textit{som}}(\mathcal{A}, M_r(\mathcal{O}_X))$
, which is an
$\mathcal{I}{\textit{som}}(\mathcal{A}, M_r(\mathcal{O}_X))$
, which is an
![]() ${\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X)) \cong{{\rm PGL}}_r$
-torsor by Corollary 2.3.
${\mathcal{A}\textit{ut}}(M_r(\mathcal{O}_X)) \cong{{\rm PGL}}_r$
-torsor by Corollary 2.3.
It is not hard to see that all
![]() ${{\rm PGL}}_r$
-torsors on
${{\rm PGL}}_r$
-torsors on
![]() $X$
are obtained in this way by a gluing argument: if a cover
$X$
are obtained in this way by a gluing argument: if a cover
![]() $\{U_i\}$
trivializes a
$\{U_i\}$
trivializes a
![]() ${{\rm PGL}}_r$
-torsor on
${{\rm PGL}}_r$
-torsor on
![]() $X$
, then the transition maps on the intersections provide exactly a gluing data to glue copies of
$X$
, then the transition maps on the intersections provide exactly a gluing data to glue copies of
![]() $\mathbb{P}^{r-1}$
into a Brauer–Severi variety over
$\mathbb{P}^{r-1}$
into a Brauer–Severi variety over
![]() $X$
(and similarly for a degree
$X$
(and similarly for a degree
![]() $r$
Azumaya algebra on
$r$
Azumaya algebra on
![]() $X$
). By a result on non-abelian cohomology [Reference GiraudGir71], the set of
$X$
). By a result on non-abelian cohomology [Reference GiraudGir71], the set of
![]() ${{\rm PGL}}_r$
-torsors on
${{\rm PGL}}_r$
-torsors on
![]() $X$
is classified by
$X$
is classified by
![]() $H^1(X,{{\rm PGL}}_r)$
.
$H^1(X,{{\rm PGL}}_r)$
.
Example 2.6. Let
![]() $E$
be a locally free sheaf of rank
$E$
be a locally free sheaf of rank
![]() $r$
on
$r$
on
![]() $X$
. Then, clearly,
$X$
. Then, clearly,
![]() $\pi : \mathbb{P}(E^\vee ) = {\rm Proj}({\rm Sym}^{\bullet }(E^\vee )) \to X$
is a degree
$\pi : \mathbb{P}(E^\vee ) = {\rm Proj}({\rm Sym}^{\bullet }(E^\vee )) \to X$
is a degree
![]() $r$
Brauer–Severi variety. It is even Zariski locally isomorphic to
$r$
Brauer–Severi variety. It is even Zariski locally isomorphic to
![]() $\mathbb{P}^{r - 1}_X$
. Then
$\mathbb{P}^{r - 1}_X$
. Then
![]() $G \cong \pi ^* E(1)$
and its associated Azumaya algebra is
$G \cong \pi ^* E(1)$
and its associated Azumaya algebra is
![]() $\mathcal{E}{\textit{nd}}(E^\vee )$
, the endomorphism sheaf. Brauer–Severi varieties of this form are called trivial because their associated category of twisted sheaves is actually untwisted, as we discuss in § 2.2.
$\mathcal{E}{\textit{nd}}(E^\vee )$
, the endomorphism sheaf. Brauer–Severi varieties of this form are called trivial because their associated category of twisted sheaves is actually untwisted, as we discuss in § 2.2.
Example 2.7. Azumaya algebras play a prominent role in number theory. Azumaya algebras over
![]() ${\rm Spec} \, k$
, where
${\rm Spec} \, k$
, where
![]() $k$
is a field, are precisely the central simple algebras over
$k$
is a field, are precisely the central simple algebras over
![]() $k$
. Thus, the quaternion algebra
$k$
. Thus, the quaternion algebra
![]() $\mathbb{H}$
is an Azumaya algebra over
$\mathbb{H}$
is an Azumaya algebra over
![]() ${{\rm Spec}}\ \mathbb{R}$
. There are no non-trivial examples for
${{\rm Spec}}\ \mathbb{R}$
. There are no non-trivial examples for
![]() $k = \mathbb{C}$
; over algebraically closed fields every Azumaya algebra is trivial. In this paper, we focus on the the case
$k = \mathbb{C}$
; over algebraically closed fields every Azumaya algebra is trivial. In this paper, we focus on the the case
![]() $k=\mathbb{C}(X)$
, where
$k=\mathbb{C}(X)$
, where
![]() $\mathbb{C}(X)$
denotes the function field of a smooth projective surface.
$\mathbb{C}(X)$
denotes the function field of a smooth projective surface.
Example 2.8. Just as for Azumaya algebras, there are no non-trivial Brauer–Severi varieties over
![]() ${{\rm Spec}}\ \mathbb{C}$
. However, over
${{\rm Spec}}\ \mathbb{C}$
. However, over
![]() ${{\rm Spec}}\ \mathbb{R}$
there is a non-trivial example, the variety
${{\rm Spec}}\ \mathbb{R}$
there is a non-trivial example, the variety
![]() $Y = Z(x^2 + y^2 + z^2) \subseteq \mathbb{P}^2_{\mathbb{R}}$
. After base change to the étale cover
$Y = Z(x^2 + y^2 + z^2) \subseteq \mathbb{P}^2_{\mathbb{R}}$
. After base change to the étale cover
![]() ${{\rm Spec}}\ \mathbb{C} \to{{\rm Spec}}\ \mathbb{R}$
,
${{\rm Spec}}\ \mathbb{C} \to{{\rm Spec}}\ \mathbb{R}$
,
![]() $Y$
is isomorphic to
$Y$
is isomorphic to
![]() $\mathbb{P}^1_{\mathbb{C}}$
. This Brauer–Severi variety corresponds to the quaternion algebra.
$\mathbb{P}^1_{\mathbb{C}}$
. This Brauer–Severi variety corresponds to the quaternion algebra.
Definition 2.9. An algebraic stack
![]() $\mathcal{G} \to X$
is called a gerbe on
$\mathcal{G} \to X$
is called a gerbe on
![]() $X$
if it satisfies the following two conditions.
$X$
if it satisfies the following two conditions.
-
(1)
 $\mathcal{G}$
admits local sections: for anyFootnote
8
$\mathcal{G}$
admits local sections: for anyFootnote
8
 $T \to X$
, there exists an étale cover
$T \to X$
, there exists an étale cover
 $\{U_i \to T\}$
such that
$\{U_i \to T\}$
such that
 $\mathcal{G}$
admits a section over each
$\mathcal{G}$
admits a section over each
 $U_i$
.
$U_i$
. -
(2) Sections of
 $\mathcal{G}$
are locally isomorphic: if
$\mathcal{G}$
are locally isomorphic: if
 $x$
,
$x$
,
 $y$
are sections of
$y$
are sections of
 $\mathcal{G}$
over some
$\mathcal{G}$
over some
 $T \to X$
, then there is an étale cover
$T \to X$
, then there is an étale cover
 $\{U_i \to T\}$
with
$\{U_i \to T\}$
with
 $x|_{U_i} \cong y|_{U_i}$
for all
$x|_{U_i} \cong y|_{U_i}$
for all
 $i$
.
$i$
.
Let
![]() $A$
be one of the groups in ‘Notation and conventions,’ viewed as a sheaf in the étale topology. An
$A$
be one of the groups in ‘Notation and conventions,’ viewed as a sheaf in the étale topology. An
![]() $A$
-gerbe on
$A$
-gerbe on
![]() $X$
is a gerbe
$X$
is a gerbe
![]() $\mathcal{G}$
on
$\mathcal{G}$
on
![]() $X$
together with an isomorphism
$X$
together with an isomorphism
![]() $\psi _{U,x} : A(U) \cong{{\rm Aut}} (x)$
for each section
$\psi _{U,x} : A(U) \cong{{\rm Aut}} (x)$
for each section
![]() $x$
of
$x$
of
![]() $\mathcal{G}$
over an étale open
$\mathcal{G}$
over an étale open
![]() $U \to T$
for any
$U \to T$
for any
![]() $T \to X$
. We require that
$T \to X$
. We require that
![]() $\psi$
is natural with respect to
$\psi$
is natural with respect to
![]() $x$
and restriction along
$x$
and restriction along
![]() $U$
. A morphism of
$U$
. A morphism of
![]() $A$
-gerbes on
$A$
-gerbes on
![]() $X$
is a morphism of stacks over
$X$
is a morphism of stacks over
![]() $X$
that commutes with
$X$
that commutes with
![]() $\psi$
.
$\psi$
.
There is also a theory of gerbes when
![]() $A$
is non-abelian, which we will not need, but see [Reference GiraudGir71], where the general theory is developed. We require the following facts from the theory of gerbes, which can all be found in [Reference GiraudGir71, Chapter IV]:
$A$
is non-abelian, which we will not need, but see [Reference GiraudGir71], where the general theory is developed. We require the following facts from the theory of gerbes, which can all be found in [Reference GiraudGir71, Chapter IV]:
Proposition 2.10.
-
1. Every morphism of
 $A$
-gerbes on
$A$
-gerbes on
 $X$
is an isomorphism
Footnote
9
. Thus, the category of
$X$
is an isomorphism
Footnote
9
. Thus, the category of
 $A$
-gerbes on
$A$
-gerbes on
 $X$
is a groupoid.
$X$
is a groupoid.
-
2. The stack of
 $A$
-torsors,
$A$
-torsors,
 $[*/A] \times X$
, forms an
$[*/A] \times X$
, forms an
 $A$
-gerbe on
$A$
-gerbe on
 $X$
. An
$X$
. An
 $A$
-gerbe on
$A$
-gerbe on
 $X$
is equivalent to this one if and only if it admits a section over
$X$
is equivalent to this one if and only if it admits a section over
 $X$
.
$X$
. -
3. The set of equivalence classes of
 $A$
-gerbes on
$A$
-gerbes on
 $X$
is canonically isomorphic to the sheaf cohomology group
$X$
is canonically isomorphic to the sheaf cohomology group
 $H^2(X,A)$
. The stack of
$H^2(X,A)$
. The stack of
 $A$
-torsors corresponds to the unit.
$A$
-torsors corresponds to the unit.
As a consequence of the proposition, and the fact that gerbes admit local sections, every
![]() $A$
-gerbe on
$A$
-gerbe on
![]() $X$
is étale locally isomorphic to the stack of
$X$
is étale locally isomorphic to the stack of
![]() $A$
-torsors
$A$
-torsors
![]() $[*/A] \times X$
. The converse is almost true:
$[*/A] \times X$
. The converse is almost true:
![]() $[*/A]$
is a group stack, and a stack over
$[*/A]$
is a group stack, and a stack over
![]() $X$
that is étale locally isomorphic to
$X$
that is étale locally isomorphic to
![]() $[*/A] \times X$
is an
$[*/A] \times X$
is an
![]() $A$
-gerbe on
$A$
-gerbe on
![]() $X$
if the gluing maps are
$X$
if the gluing maps are
![]() $[*/A]$
-equivariant.
$[*/A]$
-equivariant.
From now on, we will only be concerned with
![]() $\mathbb{G}_m$
- and
$\mathbb{G}_m$
- and
![]() $\mu _r$
-gerbes.
$\mu _r$
-gerbes.
Example 2.11. Consider the stack over
![]() $X$
, which over
$X$
, which over
![]() $T \to X$
is determined by the groupoid of line bundles on
$T \to X$
is determined by the groupoid of line bundles on
![]() $L$
on
$L$
on
![]() $T$
. This is a
$T$
. This is a
![]() $\mathbb{G}_m$
-gerbe on
$\mathbb{G}_m$
-gerbe on
![]() $X$
and it is, in fact, the trivial
$X$
and it is, in fact, the trivial
![]() $\mathbb{G}_m$
-gerbe. Indeed, it admits a global section, the trivial line bundle, and two line bundles are locally isomorphic. Moreover, there is a canonical map
$\mathbb{G}_m$
-gerbe. Indeed, it admits a global section, the trivial line bundle, and two line bundles are locally isomorphic. Moreover, there is a canonical map
![]() $\mathbb{G}_m \to{{\rm Aut}} (L)$
that provides the
$\mathbb{G}_m \to{{\rm Aut}} (L)$
that provides the
![]() $\mathbb{G}_m$
-gerbe structure.
$\mathbb{G}_m$
-gerbe structure.
Example 2.12. A typical example of a gerbe on
![]() $X$
(which we will not need) comes from the root stack construction: if
$X$
(which we will not need) comes from the root stack construction: if
![]() $L$
is a line bundle on
$L$
is a line bundle on
![]() $X$
, consider the moduli stack whose groupoid over
$X$
, consider the moduli stack whose groupoid over
![]() $T \to X$
consists of a line bundle
$T \to X$
consists of a line bundle
![]() $M$
on
$M$
on
![]() $T$
together with an isomorphism
$T$
together with an isomorphism
![]() $\phi : M^r \cong L|_T$
. This is a
$\phi : M^r \cong L|_T$
. This is a
![]() $\mu _r$
-gerbe on
$\mu _r$
-gerbe on
![]() $X$
.
$X$
.
Example 2.13. Let
![]() $Y \to X$
be a degree
$Y \to X$
be a degree
![]() $r$
Brauer–Severi variety. We consider the stack of locally free sheaves trivializing
$r$
Brauer–Severi variety. We consider the stack of locally free sheaves trivializing
![]() $Y$
: for
$Y$
: for
![]() $T \to X$
we consider the groupoid of locally free sheaves
$T \to X$
we consider the groupoid of locally free sheaves
![]() $E$
on
$E$
on
![]() $T$
together with an isomorphism
$T$
together with an isomorphism
![]() $\phi : Y|_T \cong \mathbb{P}(E^\vee )$
of
$\phi : Y|_T \cong \mathbb{P}(E^\vee )$
of
![]() $T$
-schemes. We claim this is a
$T$
-schemes. We claim this is a
![]() $\mathbb{G}_m$
-gerbe on
$\mathbb{G}_m$
-gerbe on
![]() $X$
. Indeed, this stack admits étale local sections, since
$X$
. Indeed, this stack admits étale local sections, since
![]() $Y$
is étale locally trivial. Secondly, if
$Y$
is étale locally trivial. Secondly, if
![]() $E$
and
$E$
and
![]() $F$
both trivialize
$F$
both trivialize
![]() $Y$
, then we consider the local situation where they are both free, and now we need to produce an isomorphism. The composition
$Y$
, then we consider the local situation where they are both free, and now we need to produce an isomorphism. The composition
![]() $\mathbb{P}(E^\vee ) \cong Y \cong \mathbb{P}(F^\vee )$
is given by an element of
$\mathbb{P}(E^\vee ) \cong Y \cong \mathbb{P}(F^\vee )$
is given by an element of
![]() ${{\rm PGL}}_r$
[Reference Mumford, Fogarty and KirwanMFK02, Sect. 0.5], so it is locally an equivalence class of matrices. Any matrix in this class defines an isomorphism of
${{\rm PGL}}_r$
[Reference Mumford, Fogarty and KirwanMFK02, Sect. 0.5], so it is locally an equivalence class of matrices. Any matrix in this class defines an isomorphism of
![]() $E$
and
$E$
and
![]() $F$
commuting with
$F$
commuting with
![]() $\phi$
.
$\phi$
.
If
![]() $M$
is an automorphism of
$M$
is an automorphism of
![]() $(E,\phi )$
, then it has to be a scalar: this can be checked locally, where
$(E,\phi )$
, then it has to be a scalar: this can be checked locally, where
![]() $E$
is free, and the matrix associated with
$E$
is free, and the matrix associated with
![]() $M$
acts as its representative in
$M$
acts as its representative in
![]() ${{\rm PGL}}_r$
on
${{\rm PGL}}_r$
on
![]() $\mathbb{P}(E^\vee )$
; thus, this action is trivial if and only
$\mathbb{P}(E^\vee )$
; thus, this action is trivial if and only
![]() $M$
is a non-zero scalar. This gives us a natural isomorphism
$M$
is a non-zero scalar. This gives us a natural isomorphism
![]() $\mathbb{G}_m \to{{\rm Aut}} (E,\phi )$
.
$\mathbb{G}_m \to{{\rm Aut}} (E,\phi )$
.
There is a variant on this example, where we also fix an isomorphism
![]() $\nu : \det E \cong \mathcal{O}_T$
. This restricts the number of automorphisms of the triple
$\nu : \det E \cong \mathcal{O}_T$
. This restricts the number of automorphisms of the triple
![]() $(E,\phi, \nu )$
, and the result is a
$(E,\phi, \nu )$
, and the result is a
![]() $\mu _r$
-gerbe on
$\mu _r$
-gerbe on
![]() $X$
. Thus, associated with any degree
$X$
. Thus, associated with any degree
![]() $r$
Brauer–Severi variety over
$r$
Brauer–Severi variety over
![]() $X$
is a
$X$
is a
![]() $\mathbb{G}_m$
-gerbe and a
$\mathbb{G}_m$
-gerbe and a
![]() $\mu _r$
-gerbe on
$\mu _r$
-gerbe on
![]() $X$
.
$X$
.
Example 2.14. The same example works for degree
![]() $r$
Azumaya algebras on
$r$
Azumaya algebras on
![]() $X$
: one can consider the stack of locally free sheaves
$X$
: one can consider the stack of locally free sheaves
![]() $E$
such that
$E$
such that
![]() $\mathcal{E}{\textit{nd}}(E^\vee )$
trivializes the Azumaya algebra
$\mathcal{E}{\textit{nd}}(E^\vee )$
trivializes the Azumaya algebra
![]() $\mathcal{A}$
, both with and without trivializing the determinant. In this case the Skolem–Noether theorem ensures that we can use the group
$\mathcal{A}$
, both with and without trivializing the determinant. In this case the Skolem–Noether theorem ensures that we can use the group
![]() ${{\rm PGL}}_r$
in the same way as above. In fact, by the result of Proposition 2.5 and Example 2.6, a locally free sheaf
${{\rm PGL}}_r$
in the same way as above. In fact, by the result of Proposition 2.5 and Example 2.6, a locally free sheaf
![]() $E$
trivializes
$E$
trivializes
![]() $\mathcal{A}$
if and only if it trivializes the associated Brauer–Severi variety, so the moduli stacks of these examples are isomorphic.
$\mathcal{A}$
if and only if it trivializes the associated Brauer–Severi variety, so the moduli stacks of these examples are isomorphic.
By the previous examples, every Brauer–Severi variety
![]() $Y$
on
$Y$
on
![]() $X$
of degree
$X$
of degree
![]() $r$
defines classes
$r$
defines classes
![]() $\alpha (Y) \in H^2(X, \mathbb{G}_m)$
and
$\alpha (Y) \in H^2(X, \mathbb{G}_m)$
and
![]() $w(Y) \in H^2(X, \mu _r)$
. We refer to
$w(Y) \in H^2(X, \mu _r)$
. We refer to
![]() $\alpha (Y)$
as the Brauer class of
$\alpha (Y)$
as the Brauer class of
![]() $Y$
and to
$Y$
and to
![]() $w(Y)$
as the Stiefel–Whitney class of
$w(Y)$
as the Stiefel–Whitney class of
![]() $Y$
. Similarly, every Azumaya algebra
$Y$
. Similarly, every Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
of degree
$X$
of degree
![]() $r$
determines classes
$r$
determines classes
![]() $\alpha (\mathcal{A}) \in H^2(X, \mathbb{G}_m)$
and
$\alpha (\mathcal{A}) \in H^2(X, \mathbb{G}_m)$
and
![]() $w(\mathcal{A}) \in H^2(X, \mu _r)$
. The assignments
$w(\mathcal{A}) \in H^2(X, \mu _r)$
. The assignments
![]() $Y \mapsto w(Y)$
and
$Y \mapsto w(Y)$
and
![]() $Y \mapsto \alpha (Y)$
fit in the framework of non-abelian cohomology [Reference GiraudGir71]. This theory defines groups
$Y \mapsto \alpha (Y)$
fit in the framework of non-abelian cohomology [Reference GiraudGir71]. This theory defines groups
![]() $H^1(X, G)$
and
$H^1(X, G)$
and
![]() $H^2(X, G)$
for non-abelian groups
$H^2(X, G)$
for non-abelian groups
![]() $G$
in the étale topology, and defines connecting homomorphisms between these groups. The definitions of the connecting homomorphisms induced by the sequences
$G$
in the étale topology, and defines connecting homomorphisms between these groups. The definitions of the connecting homomorphisms induced by the sequences
are precisely
![]() $w$
and
$w$
and
![]() $\alpha$
. Furthermore, these maps are compatible in the sense that the following diagram commutes:
$\alpha$
. Furthermore, these maps are compatible in the sense that the following diagram commutes:
where
![]() $o$
is induced by the inclusion
$o$
is induced by the inclusion
![]() $\mu _r \leq \mathbb{G}_m$
. This can be seen by either using that there is a morphism between the short exact sequences from (3), or, alternatively, by explicitly comparing the gerbes. Note that the vertical arrow
$\mu _r \leq \mathbb{G}_m$
. This can be seen by either using that there is a morphism between the short exact sequences from (3), or, alternatively, by explicitly comparing the gerbes. Note that the vertical arrow
![]() $o$
in the diagram is part of the long exact sequences induced by the Kummer sequence
$o$
in the diagram is part of the long exact sequences induced by the Kummer sequence
Since
![]() $H^1(X,\mathbb{G}_m) \cong {\rm Pic}(X)$
, we refer to the first map as
$H^1(X,\mathbb{G}_m) \cong {\rm Pic}(X)$
, we refer to the first map as
![]() $c_1 : H^1(X,\mathbb{G}_m) \to H^2(X,\mu _r)$
. In the trivial case we get [Reference YoshiokaYos06, Lemma 1.2], [Reference Huybrechts and SchröerHS03]
$c_1 : H^1(X,\mathbb{G}_m) \to H^2(X,\mu _r)$
. In the trivial case we get [Reference YoshiokaYos06, Lemma 1.2], [Reference Huybrechts and SchröerHS03]
By the comparison theorem [Reference MilneMil80], the étale cohomology group
![]() $H^2(X,\mu _r)$
equals the corresponding singular cohomology group with respect to the complex analytic topology on
$H^2(X,\mu _r)$
equals the corresponding singular cohomology group with respect to the complex analytic topology on
![]() $X$
, which we sometimes denote by
$X$
, which we sometimes denote by
![]() $H^2(X,\mathbb{Z} / r\mathbb{Z})$
. The above factorization (4) also reveals that the Brauer class of a degree
$H^2(X,\mathbb{Z} / r\mathbb{Z})$
. The above factorization (4) also reveals that the Brauer class of a degree
![]() $r$
Azumaya algebra on
$r$
Azumaya algebra on
![]() $X$
is an
$X$
is an
![]() $r$
-torsion element of
$r$
-torsion element of
![]() $H^2(X,\mathbb{G}_m)$
.
$H^2(X,\mathbb{G}_m)$
.
In the next section, we assume
![]() $H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
(in the complex analytic topology). Then, by Lemma 3.1, we have
$H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
(in the complex analytic topology). Then, by Lemma 3.1, we have
Using the identification
![]() $H^1(X,\mathbb{G}_m) \cong {\rm Pic}(X)$
, the map
$H^1(X,\mathbb{G}_m) \cong {\rm Pic}(X)$
, the map
![]() $H^1(X,\mathbb{G}_m) \to H^2(X,\mu _r)$
factors via the usual first Chern class map
$H^1(X,\mathbb{G}_m) \to H^2(X,\mu _r)$
factors via the usual first Chern class map
![]()
where the diagonal arrow is the quotient map and the vertical arrow is surjective by the Lefschetz theorem on
![]() $(1,1)$
-classes. By the Kummer sequence (5), the
$(1,1)$
-classes. By the Kummer sequence (5), the
![]() $\mu _r$
-gerbes which are trivial as
$\mu _r$
-gerbes which are trivial as
![]() $\mathbb{G}_m$
-gerbes are precisely the elements of
$\mathbb{G}_m$
-gerbes are precisely the elements of
The cohomology class
![]() $\alpha (Y) \in H^2(X, \mathbb{G}_m)$
determines whether
$\alpha (Y) \in H^2(X, \mathbb{G}_m)$
determines whether
![]() $Y$
is trivial (in the sense of Example 2.6), because
$Y$
is trivial (in the sense of Example 2.6), because
![]() $\alpha (Y)=0$
if and only if the gerbe from Example 2.13 has a global section (Proposition 2.10), but this precisely happens when a trivialising locally free sheaf exists on
$\alpha (Y)=0$
if and only if the gerbe from Example 2.13 has a global section (Proposition 2.10), but this precisely happens when a trivialising locally free sheaf exists on
![]() $X$
. This statement can also be seen from the previous paragraph combined with [Reference YoshiokaYos06, Lemma 1.4].Footnote
10
$X$
. This statement can also be seen from the previous paragraph combined with [Reference YoshiokaYos06, Lemma 1.4].Footnote
10
It is not possible to recover a Brauer–Severi variety from its class in
![]() $H^2(X, \mathbb{G}_m)$
; indeed, all Brauer–Severi varieties of the form
$H^2(X, \mathbb{G}_m)$
; indeed, all Brauer–Severi varieties of the form
![]() $\mathbb{P}(E^\vee )$
for some locally free sheaf
$\mathbb{P}(E^\vee )$
for some locally free sheaf
![]() $E$
have trivial class. Thus, taking the associated class is not ‘injective’. Instead, we have the following ’surjectivity‘ results.
$E$
have trivial class. Thus, taking the associated class is not ‘injective’. Instead, we have the following ’surjectivity‘ results.
Theorem 2.15. (de Jong). Any torsion class in
![]() $H^2(X, \mathbb{G}_m)$
is equal to
$H^2(X, \mathbb{G}_m)$
is equal to
![]() $\alpha (Y)$
for some Brauer–Severi variety
$\alpha (Y)$
for some Brauer–Severi variety
![]() $Y \to X$
.
$Y \to X$
.
Theorem 2.16. (de Jong, Lieblich). Suppose
![]() $\dim (X)=2$
. Any class in
$\dim (X)=2$
. Any class in
![]() $H^2(X, \mu _r)$
is equal to
$H^2(X, \mu _r)$
is equal to
![]() $w(Y)$
for some degree
$w(Y)$
for some degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
.
$Y \to X$
.
Theorem 2.15 holds far more generally. We only need
![]() $X$
to admit an ample line bundle, for example, if
$X$
to admit an ample line bundle, for example, if
![]() $X$
is quasi-projective over an affine scheme (see [Reference de JongdJo]). On the contrary, Theorem 2.16 is special in the sense that it does not hold for smooth varieties of arbitrary dimension [Reference Antieau and WilliamsAW14]. It is a consequence of the period-index theorem proved by de Jong [Reference de JongdJo04]. See [Reference LieblichLie08, Corollary 4.2.2.4] on how to deduce this specific form of the theorem.
$X$
is quasi-projective over an affine scheme (see [Reference de JongdJo]). On the contrary, Theorem 2.16 is special in the sense that it does not hold for smooth varieties of arbitrary dimension [Reference Antieau and WilliamsAW14]. It is a consequence of the period-index theorem proved by de Jong [Reference de JongdJo04]. See [Reference LieblichLie08, Corollary 4.2.2.4] on how to deduce this specific form of the theorem.
2.2 Twisted sheaves
We review the theory of twisted sheaves from different viewpoints. Recall the sheaf
![]() $G$
from Lemma 2.4.
$G$
from Lemma 2.4.
Definition 2.17. Let
![]() $\pi : Y \to X$
be a BrauerSeveri variety. A
$\pi : Y \to X$
be a BrauerSeveri variety. A
![]() $Y$
-sheaf is a coherent sheaf
$Y$
-sheaf is a coherent sheaf
![]() $F$
on
$F$
on
![]() $Y$
such that the counit
$Y$
such that the counit
![]() $\pi ^*\pi _*(F \otimes G^\vee ) \to F \otimes G^\vee$
is an isomorphism. The category of
$\pi ^*\pi _*(F \otimes G^\vee ) \to F \otimes G^\vee$
is an isomorphism. The category of
![]() $Y$
-sheaves is denoted
$Y$
-sheaves is denoted
![]() ${{\rm Coh}}(X,Y)$
. Let
${{\rm Coh}}(X,Y)$
. Let
![]() $\mathcal{A}$
be an Azumaya algebra on
$\mathcal{A}$
be an Azumaya algebra on
![]() $X$
. An
$X$
. An
![]() $\mathcal{A}$
-module is a left module over
$\mathcal{A}$
-module is a left module over
![]() $\mathcal{A}$
such that the underlying
$\mathcal{A}$
such that the underlying
![]() $\mathcal{O}_X$
-module is coherent. The category of
$\mathcal{O}_X$
-module is coherent. The category of
![]() $\mathcal{A}$
-modules is denoted
$\mathcal{A}$
-modules is denoted
![]() ${{\rm Coh}}(X,\mathcal{A})$
.
${{\rm Coh}}(X,\mathcal{A})$
.
Proposition 2.18. (Reede). Let
![]() $\pi : Y \to X$
be a Brauer–Severi variety over
$\pi : Y \to X$
be a Brauer–Severi variety over
![]() $X$
with corresponding Azumaya algebra
$X$
with corresponding Azumaya algebra
![]() $\mathcal{A}$
(Proposition 2.5). Then there is a canonical equivalence between
$\mathcal{A}$
(Proposition 2.5). Then there is a canonical equivalence between
![]() ${{\rm Coh}}(X,\mathcal{A})$
and
${{\rm Coh}}(X,\mathcal{A})$
and
![]() ${{\rm Coh}}(X, Y)$
.
${{\rm Coh}}(X, Y)$
.
Proof.
Let us describe the equivalence. If
![]() $F$
is a
$F$
is a
![]() $Y$
-sheaf, then
$Y$
-sheaf, then
![]() $\mathcal{H}{\textit{om}}(G, F)$
is a
$\mathcal{H}{\textit{om}}(G, F)$
is a
![]() $\mathcal{E}{\textit{nd}}(G^\vee )$
-module. Hence
$\mathcal{E}{\textit{nd}}(G^\vee )$
-module. Hence
![]() $\pi _*(\mathcal{H}{\textit{om}}(G, F))$
is a
$\pi _*(\mathcal{H}{\textit{om}}(G, F))$
is a
![]() $\pi _* \mathcal{E}{\textit{nd}}(G^\vee )$
module, but the latter is identified with
$\pi _* \mathcal{E}{\textit{nd}}(G^\vee )$
module, but the latter is identified with
![]() $\mathcal{A}$
. On the other hand, if
$\mathcal{A}$
. On the other hand, if
![]() $F$
is a
$F$
is a
![]() $\pi _* \mathcal{E}{\textit{nd}}(G^\vee )$
-module, then
$\pi _* \mathcal{E}{\textit{nd}}(G^\vee )$
-module, then
![]() $\pi ^*F$
is a
$\pi ^*F$
is a
![]() $\pi ^*\pi _* \mathcal{E}{\textit{nd}}(G^\vee ) \cong \mathcal{E}{\textit{nd}}(G^\vee )$
-module (Lemma 2.4). Hence it is a right
$\pi ^*\pi _* \mathcal{E}{\textit{nd}}(G^\vee ) \cong \mathcal{E}{\textit{nd}}(G^\vee )$
-module (Lemma 2.4). Hence it is a right
![]() $\mathcal{E}{\textit{nd}}(G)$
-module. Then
$\mathcal{E}{\textit{nd}}(G)$
-module. Then
![]() $\pi ^*F \otimes _{\mathcal{E}{\textit{nd}}(G)} G$
is the corresponding
$\pi ^*F \otimes _{\mathcal{E}{\textit{nd}}(G)} G$
is the corresponding
![]() $Y$
-sheaf. Reede checks that this is an equivalence [Reference ReedeRee18, Lemma 1.10].
$Y$
-sheaf. Reede checks that this is an equivalence [Reference ReedeRee18, Lemma 1.10].
The category of
![]() $Y$
-sheaves only depends on
$Y$
-sheaves only depends on
![]() $\alpha (Y) \in H^2(X, \mathbb{G}_m)$
. We review the theory of coherent sheaves on gerbes and explain how to recover
$\alpha (Y) \in H^2(X, \mathbb{G}_m)$
. We review the theory of coherent sheaves on gerbes and explain how to recover
![]() ${{\rm Coh}}(X,\mathcal{A})$
,
${{\rm Coh}}(X,\mathcal{A})$
,
![]() ${{\rm Coh}}(X,Y)$
. The following result can be found in work of Lieblich [Reference LieblichLie07, Propositions 2.1.1.13, 2.2.1.6].
${{\rm Coh}}(X,Y)$
. The following result can be found in work of Lieblich [Reference LieblichLie07, Propositions 2.1.1.13, 2.2.1.6].
Proposition 2.19. (Lieblich). Let
![]() $\pi : \mathcal{G} \to X$
be a
$\pi : \mathcal{G} \to X$
be a
![]() $\mathbb{G}_m$
-gerbe. Every quasi-coherent sheaf
$\mathbb{G}_m$
-gerbe. Every quasi-coherent sheaf
![]() $F$
on
$F$
on
![]() $\mathcal{G}$
admits a canonical
$\mathcal{G}$
admits a canonical
![]() $\mathbb{G}_m$
-action. Hence, it admits a functorial weight decomposition
$\mathbb{G}_m$
-action. Hence, it admits a functorial weight decomposition
In fact, the entire category of quasi-coherent sheaves admits a weight decomposition
Furthermore, the pull-back
![]() $\pi ^* : {\rm QCoh}(X) \to {\rm QCoh}(\mathcal{G})$
induces an equivalence between
$\pi ^* : {\rm QCoh}(X) \to {\rm QCoh}(\mathcal{G})$
induces an equivalence between
![]() ${\rm QCoh}(X)$
and
${\rm QCoh}(X)$
and
![]() ${\rm QCoh}(\mathcal{G})_0$
, these are the sheaves on which the action is trivial. For a
${\rm QCoh}(\mathcal{G})_0$
, these are the sheaves on which the action is trivial. For a
![]() $\mu _r$
-gerbe the same result holds, except that the grading is now over
$\mu _r$
-gerbe the same result holds, except that the grading is now over
![]() $\mathbb{Z}/r\mathbb{Z}$
.
$\mathbb{Z}/r\mathbb{Z}$
.
Tensor product and
![]() $\mathcal{H}{\textit{om}}$
respects this decomposition, in the sense that if
$\mathcal{H}{\textit{om}}$
respects this decomposition, in the sense that if
![]() $F \in {\rm QCoh}(\mathcal{G})_n$
and
$F \in {\rm QCoh}(\mathcal{G})_n$
and
![]() $F^{\prime} \in {\rm QCoh}(\mathcal{G})_m$
, then
$F^{\prime} \in {\rm QCoh}(\mathcal{G})_m$
, then
![]() $F \otimes F^{\prime} \in {\rm QCoh}(\mathcal{G})_{n+m}$
and
$F \otimes F^{\prime} \in {\rm QCoh}(\mathcal{G})_{n+m}$
and
![]() $\mathcal{H}{\textit{om}}(F, F^{\prime}) \in {\rm QCoh}(\mathcal{G})_{-n+m}$
. In particular, if
$\mathcal{H}{\textit{om}}(F, F^{\prime}) \in {\rm QCoh}(\mathcal{G})_{-n+m}$
. In particular, if
![]() $F$
is of pure weight, then
$F$
is of pure weight, then
![]() $\mathcal{H}{\textit{om}}(F, F)$
is of weight zero and thus descends to
$\mathcal{H}{\textit{om}}(F, F)$
is of weight zero and thus descends to
![]() $X$
.
$X$
.
Definition 2.20. If
![]() $\pi : \mathcal{G} \to X$
is a
$\pi : \mathcal{G} \to X$
is a
![]() $\mathbb{G}_m$
-gerbe, we define the
$\mathbb{G}_m$
-gerbe, we define the
![]() $\mathcal{G}$
-twisted sheaves as the coherent objects of
$\mathcal{G}$
-twisted sheaves as the coherent objects of
![]() ${\rm QCoh}(\mathcal{G})_1$
. We denote the category of
${\rm QCoh}(\mathcal{G})_1$
. We denote the category of
![]() $\mathcal{G}$
-twisted sheaves by
$\mathcal{G}$
-twisted sheaves by
![]() ${{\rm Coh}}(\mathcal{G})_1$
. We make analogous definitions for a
${{\rm Coh}}(\mathcal{G})_1$
. We make analogous definitions for a
![]() $\mu _r$
-gerbe on
$\mu _r$
-gerbe on
![]() $X$
, except now
$X$
, except now
![]() $1 \in \mathbb{Z}/r\mathbb{Z}$
.
$1 \in \mathbb{Z}/r\mathbb{Z}$
.
Let
![]() $\mathcal{A}$
be an Azumaya algebra on
$\mathcal{A}$
be an Azumaya algebra on
![]() $X$
mapping to a
$X$
mapping to a
![]() $\mathbb{G}_m$
-gerbe
$\mathbb{G}_m$
-gerbe
![]() $\pi : \mathcal{G} \to X$
. Then there exists a rank
$\pi : \mathcal{G} \to X$
. Then there exists a rank
![]() $r$
locally free sheaf
$r$
locally free sheaf
![]() $E$
on
$E$
on
![]() $\mathcal{G}$
such that
$\mathcal{G}$
such that
![]() $\mathcal{E}{\textit{nd}}(E^\vee ) \cong \mathcal{A}|_{\mathcal{G}}$
. One can verify that
$\mathcal{E}{\textit{nd}}(E^\vee ) \cong \mathcal{A}|_{\mathcal{G}}$
. One can verify that
![]() $E$
is in fact a twisted sheaf [Reference LieblichLie07, Corollary 2.2.2.2]. If
$E$
is in fact a twisted sheaf [Reference LieblichLie07, Corollary 2.2.2.2]. If
![]() $F$
is any
$F$
is any
![]() $\mathcal{G}$
-twisted sheaf, then
$\mathcal{G}$
-twisted sheaf, then
![]() $\mathcal{H}{\textit{om}}(E, F)$
is again untwisted, i.e. it is (uniquely) in the image of
$\mathcal{H}{\textit{om}}(E, F)$
is again untwisted, i.e. it is (uniquely) in the image of
![]() $\pi ^*$
by Proposition 2.19. Note that
$\pi ^*$
by Proposition 2.19. Note that
![]() $\mathcal{H}{\textit{om}}(E, F)$
is a right
$\mathcal{H}{\textit{om}}(E, F)$
is a right
![]() $\mathcal{E}{\textit{nd}}(E)$
-module and therefore a left
$\mathcal{E}{\textit{nd}}(E)$
-module and therefore a left
![]() $\mathcal{E}{\textit{nd}}(E)^{{\rm op}} \cong \mathcal{E}{\textit{nd}}(E^\vee )$
-module. The following is a consequence of Morita equivalence [Reference CăldăraruCal00, Reference LieblichLie07].
$\mathcal{E}{\textit{nd}}(E)^{{\rm op}} \cong \mathcal{E}{\textit{nd}}(E^\vee )$
-module. The following is a consequence of Morita equivalence [Reference CăldăraruCal00, Reference LieblichLie07].
Proposition 2.21.
Let
![]() $\mathcal{A}$
be an Azumaya algebra on
$\mathcal{A}$
be an Azumaya algebra on
![]() $X$
mapping to a
$X$
mapping to a
![]() $\mathbb{G}_m$
-gerbe
$\mathbb{G}_m$
-gerbe
![]() $\mathcal{G} \to X$
. The assignment
$\mathcal{G} \to X$
. The assignment
![]() $F \mapsto \pi _* \mathcal{H}{\textit{om}}(E, F)$
gives an equivalence between
$F \mapsto \pi _* \mathcal{H}{\textit{om}}(E, F)$
gives an equivalence between
![]() ${{\rm Coh}}(\mathcal{G})_1$
and
${{\rm Coh}}(\mathcal{G})_1$
and
![]() ${{\rm Coh}}(X,\mathcal{A})$
.
${{\rm Coh}}(X,\mathcal{A})$
.
This discussion also works for the associated
![]() $\mu _r$
-gerbe, instead of the
$\mu _r$
-gerbe, instead of the
![]() $\mathbb{G}_m$
-gerbe.
$\mathbb{G}_m$
-gerbe.
In summary, for a Brauer–Severi variety
![]() $Y \to X$
with corresponding Azumaya algebra
$Y \to X$
with corresponding Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
with corresponding
$X$
with corresponding
![]() $\mathbb{G}_m$
-gerbe
$\mathbb{G}_m$
-gerbe
![]() $\mathcal{G}$
, we have the three equivalent categories
$\mathcal{G}$
, we have the three equivalent categories
which in particular shows that (up to equivalence) the category only depends on the gerbe
![]() $\mathcal{G}$
. In the next section, we view the
$\mathcal{G}$
. In the next section, we view the
![]() $\mathbb{G}_m$
-gerbe
$\mathbb{G}_m$
-gerbe
![]() $\mathcal{G}$
as a Brauer class and establish in a different way that
$\mathcal{G}$
as a Brauer class and establish in a different way that
![]() ${{\rm Coh}}(X,\mathcal{A})$
only depends on this Brauer class (Example 2.25). In view of this discussion, it seems reasonable to call any of these equivalent categories the category of twisted sheaves.
${{\rm Coh}}(X,\mathcal{A})$
only depends on this Brauer class (Example 2.25). In view of this discussion, it seems reasonable to call any of these equivalent categories the category of twisted sheaves.
2.3 Brauer group
The material of the previous sections is closely related to the Brauer group. We review its most important properties.
Definition 2.22. Define two Azumaya algebras
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{A}^{\prime}$
on
$\mathcal{A}^{\prime}$
on
![]() $X$
to be Brauer equivalent if there exist locally free sheaves
$X$
to be Brauer equivalent if there exist locally free sheaves
![]() $E$
and
$E$
and
![]() $E^{\prime}$
of finite rank on
$E^{\prime}$
of finite rank on
![]() $X$
such that
$X$
such that
![]() $\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E) \cong \mathcal{A}^{\prime} \otimes \mathcal{E}{\textit{nd}}(E^{\prime})$
. The resulting equivalence classes form a group, where
$\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E) \cong \mathcal{A}^{\prime} \otimes \mathcal{E}{\textit{nd}}(E^{\prime})$
. The resulting equivalence classes form a group, where
![]() $[\mathcal{A}] + [\mathcal{A}^{\prime}] = [\mathcal{A} \otimes \mathcal{A}^{\prime}]$
and the inverse of
$[\mathcal{A}] + [\mathcal{A}^{\prime}] = [\mathcal{A} \otimes \mathcal{A}^{\prime}]$
and the inverse of
![]() $[\mathcal{A}]$
is
$[\mathcal{A}]$
is
![]() $[\mathcal{A}^{{\rm op}}]$
. This group is called the Brauer group
$[\mathcal{A}^{{\rm op}}]$
. This group is called the Brauer group
![]() ${\rm Br}(X)$
of
${\rm Br}(X)$
of
![]() $X$
. For any
$X$
. For any
![]() $r\gt 1$
, we have a natural homomorphism
$r\gt 1$
, we have a natural homomorphism
![]() $H^1(X,{\rm PGL}_r) \to {\rm Br}(X)$
.
$H^1(X,{\rm PGL}_r) \to {\rm Br}(X)$
.
The fact that the inverse is given by the opposite algebra follows from an alternative definition of Azumaya algebras as coherent
![]() $\mathcal{O}_X$
-algebras
$\mathcal{O}_X$
-algebras
![]() $\mathcal{A}$
, which are locally free, and for which
$\mathcal{A}$
, which are locally free, and for which
is an isomorphism.
Proposition 2.23.
The map
![]() $H^1(X,{\rm PGL}_r) \to H^2(X,\mathbb{G}_m)$
descends to an injective homomorphism
$H^1(X,{\rm PGL}_r) \to H^2(X,\mathbb{G}_m)$
descends to an injective homomorphism
![]() ${\rm Br}(X) \to H^2(X, \mathbb{G}_m)$
. Its image is exactly the collection of torsion classes in
${\rm Br}(X) \to H^2(X, \mathbb{G}_m)$
. Its image is exactly the collection of torsion classes in
![]() $H^2(X, \mathbb{G}_m)$
.
$H^2(X, \mathbb{G}_m)$
.
Proof.
It suffices to show that for any Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
and locally free sheaf
$X$
and locally free sheaf
![]() $E$
of finite rank on
$E$
of finite rank on
![]() $X$
, the
$X$
, the
![]() $\mathbb{G}_m$
-gerbes associated with
$\mathbb{G}_m$
-gerbes associated with
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
are equivalent. This is done as follows: if a locally free sheaf
$\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
are equivalent. This is done as follows: if a locally free sheaf
![]() $E^{\prime}$
on a scheme
$E^{\prime}$
on a scheme
![]() $T \to X$
trivializes
$T \to X$
trivializes
![]() $\mathcal{A}$
, then
$\mathcal{A}$
, then
![]() $E^{\prime} \otimes E$
trivializes
$E^{\prime} \otimes E$
trivializes
![]() $\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
. This defines a
$\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
. This defines a
![]() $\mathbb{G}_m$
-equivariant morphism between gerbes, which is therefore an isomorphism (Proposition 2.10).
$\mathbb{G}_m$
-equivariant morphism between gerbes, which is therefore an isomorphism (Proposition 2.10).
By (3), the kernel of the map
![]() $\alpha : H^1(X,{{\rm PGL}}_r) \to H^2(X,\mathbb{G}_m)$
is the image of
$\alpha : H^1(X,{{\rm PGL}}_r) \to H^2(X,\mathbb{G}_m)$
is the image of
![]() $H^1(X,{\rm GL}_r) \to H^1(X,{{\rm PGL}}_r)$
, which precisely consists of trivial Azumaya algebras
$H^1(X,{\rm GL}_r) \to H^1(X,{{\rm PGL}}_r)$
, which precisely consists of trivial Azumaya algebras
![]() $\mathcal{A} \cong \mathcal{E}{\textit{nd}}(E)$
on
$\mathcal{A} \cong \mathcal{E}{\textit{nd}}(E)$
on
![]() $X$
, from which the injectivity statement follows.
$X$
, from which the injectivity statement follows.
By (4), any element in the image of
![]() $\alpha$
is torsion. Moreover, all torsion elements of
$\alpha$
is torsion. Moreover, all torsion elements of
![]() $H^2(X,\mathbb{G}_m)$
are in the image by Theorem 2.15.
$H^2(X,\mathbb{G}_m)$
are in the image by Theorem 2.15.
Remark 2.24. For a Noetherian scheme
![]() $Z$
, the torsion part of
$Z$
, the torsion part of
![]() $H^2(Z, \mathbb{G}_m)$
is also known as the cohomological Brauer group of
$H^2(Z, \mathbb{G}_m)$
is also known as the cohomological Brauer group of
![]() $Z$
. For a regular Noetherian scheme
$Z$
. For a regular Noetherian scheme
![]() $Z$
,
$Z$
,
![]() $H^2(Z, \mathbb{G}_m)$
is a torsion group [Reference MilneMil80, Corollary IV.2.6], [ Reference LieblichLie08, Corollary 3.1.3.4], so in our setting,
$H^2(Z, \mathbb{G}_m)$
is a torsion group [Reference MilneMil80, Corollary IV.2.6], [ Reference LieblichLie08, Corollary 3.1.3.4], so in our setting,
![]() ${\rm Br}(X) \cong H^2(X, \mathbb{G}_m)$
.
${\rm Br}(X) \cong H^2(X, \mathbb{G}_m)$
.
From Proposition 2.21 one can see that the category of left
![]() $\mathcal{A}$
-modules only depends on the Brauer class of
$\mathcal{A}$
-modules only depends on the Brauer class of
![]() $\mathcal{A}$
. One can also see this explicitly as follows.
$\mathcal{A}$
. One can also see this explicitly as follows.
Example 2.25. For an Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
and locally free sheaf
$X$
and locally free sheaf
![]() $E$
of finite rank on
$E$
of finite rank on
![]() $X$
, we want to show that
$X$
, we want to show that
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{A} \otimes \mathcal{E}nd(E)$
have equivalent categories of left modules. This follows from Morita theory [Reference LamLam99, §18D]. Indeed,
$\mathcal{A} \otimes \mathcal{E}nd(E)$
have equivalent categories of left modules. This follows from Morita theory [Reference LamLam99, §18D]. Indeed,
![]() $\mathcal{A} \otimes \mathcal{E}nd(E)$
is a
$\mathcal{A} \otimes \mathcal{E}nd(E)$
is a
![]() $(\mathcal{A}, \mathcal{A}\otimes \mathcal{E}{\textit{nd}}(E))$
bimodule, which is locally free both as
$(\mathcal{A}, \mathcal{A}\otimes \mathcal{E}{\textit{nd}}(E))$
bimodule, which is locally free both as
![]() $\mathcal{A}$
- and
$\mathcal{A}$
- and
![]() $\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
-module. Explicitly, the functor
$\mathcal{A} \otimes \mathcal{E}{\textit{nd}}(E)$
-module. Explicitly, the functor
is an equivalence.
One might wonder if the converse is true: if
![]() $\mathcal{A}$
and
$\mathcal{A}$
and
![]() $\mathcal{A}^{\prime}$
are such that their categories of modules are equivalent, are they also Brauer equivalent? Căldăraru’s conjecture, now a theorem [Reference AntieauAnt16], says that this is almost the case.
$\mathcal{A}^{\prime}$
are such that their categories of modules are equivalent, are they also Brauer equivalent? Căldăraru’s conjecture, now a theorem [Reference AntieauAnt16], says that this is almost the case.
Theorem 2.26. (Antieau). Let
![]() $X$
and
$X$
and
![]() $Y$
be quasi-compact and quasi-separated schemes over a commutative ring
$Y$
be quasi-compact and quasi-separated schemes over a commutative ring
![]() $R$
. Suppose that
$R$
. Suppose that
![]() $\mathcal{A}_X$
and
$\mathcal{A}_X$
and
![]() $\mathcal{A}_Y$
are Azumaya algebras on
$\mathcal{A}_Y$
are Azumaya algebras on
![]() $X$
, respectively
$X$
, respectively
![]() $Y$
, such that there is an
$Y$
, such that there is an
![]() $R$
-linear equivalence between
$R$
-linear equivalence between
![]() ${\rm QCoh}(\mathcal{A}_X)$
and
${\rm QCoh}(\mathcal{A}_X)$
and
![]() ${\rm QCoh}(\mathcal{A}_Y)$
. Then there is an isomorphism
${\rm QCoh}(\mathcal{A}_Y)$
. Then there is an isomorphism
![]() $\varphi : X \to Y$
of
$\varphi : X \to Y$
of
![]() $R$
-schemes such that
$R$
-schemes such that
![]() $\varphi ^*\mathcal{A}_Y$
is Brauer equivalent to
$\varphi ^*\mathcal{A}_Y$
is Brauer equivalent to
![]() $\mathcal{A}_X$
.
$\mathcal{A}_X$
.
3. Moduli of twisted sheaves
3.1 Chern characters
From now on we will in addition assume that
![]() $\dim (X)=2$
, i.e.
$\dim (X)=2$
, i.e.
![]() $X$
is a surface, and that
$X$
is a surface, and that
![]() $H_1(X, \mathbb{Z})$
is torsion free (in the complex analytic topology). By Poincaré duality and the universal coefficient theorem, this implies that all groups
$H_1(X, \mathbb{Z})$
is torsion free (in the complex analytic topology). By Poincaré duality and the universal coefficient theorem, this implies that all groups
![]() $H_i(X,\mathbb{Z})$
,
$H_i(X,\mathbb{Z})$
,
![]() $H^i(X,\mathbb{Z})$
are torsion free.
$H^i(X,\mathbb{Z})$
are torsion free.
In the next lemma, we use the assumption that
![]() $H_1(X, \mathbb{Z})$
is torsion free to construct lifts of Stiefel–Whitney classes.
$H_1(X, \mathbb{Z})$
is torsion free to construct lifts of Stiefel–Whitney classes.
Lemma 3.1.
There is an isomorphism
![]() $H^2(X, \mathbb{Z})/rH^2(X, \mathbb{Z}) \cong H^2(X, \mu _r)$
induced by the long exact sequence associated with the short exact sequence
$H^2(X, \mathbb{Z})/rH^2(X, \mathbb{Z}) \cong H^2(X, \mu _r)$
induced by the long exact sequence associated with the short exact sequence
where
![]() $\mathbb{Z} / r\mathbb{Z} \cong \mu _r$
. In other words, every
$\mathbb{Z} / r\mathbb{Z} \cong \mu _r$
. In other words, every
![]() $w \in H^2(X, \mu _r)$
is represented by a
$w \in H^2(X, \mu _r)$
is represented by a
![]() $\xi \in H^2(X, \mathbb{Z})$
, which is unique up to translation by multiples of
$\xi \in H^2(X, \mathbb{Z})$
, which is unique up to translation by multiples of
![]() $r$
.
$r$
.
Proof.
By using the long exact sequence, it suffices to show that
![]() $H^2(X, \mu _r) \to H^3(X, \mathbb{Z})$
is zero. Since the first group is torsion, it suffices to prove that
$H^2(X, \mu _r) \to H^3(X, \mathbb{Z})$
is zero. Since the first group is torsion, it suffices to prove that
![]() $H^3(X, \mathbb{Z})$
is torsion free. This follows from Poincaré duality and the assumption that
$H^3(X, \mathbb{Z})$
is torsion free. This follows from Poincaré duality and the assumption that
![]() $H_1(X, \mathbb{Z})$
is torsion free.
$H_1(X, \mathbb{Z})$
is torsion free.
Another important consequence of the assumption
![]() $H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
is that for any Brauer–Severi variety
$H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
is that for any Brauer–Severi variety
![]() $\pi : Y \to X$
, the map
$\pi : Y \to X$
, the map
is an inclusion [Reference YoshiokaYos06, Lemma 1.6].
The lifts of Lemma 3.1 are used to define the Chern character of twisted sheaves. This definition is due to Yoshioka [Reference YoshiokaYos06]. On surfaces this gives the correct answer (due to Proposition 3.3, and the discussion at the end of this section), but for higher-dimensional varieties another definition is required.
Definition 3.2. If
![]() $\mathcal{A}$
is an Azumaya algebra on a surface
$\mathcal{A}$
is an Azumaya algebra on a surface
![]() $X$
, choose a representing element
$X$
, choose a representing element
![]() $\xi \in H^2(X,\mathbb{Z})$
for
$\xi \in H^2(X,\mathbb{Z})$
for
![]() $w(\mathcal{A}) \in H^2(X,\mu _r)$
(Lemma 3.1). If
$w(\mathcal{A}) \in H^2(X,\mu _r)$
(Lemma 3.1). If
![]() $F$
is a left
$F$
is a left
![]() $\mathcal{A}$
-module, we define
$\mathcal{A}$
-module, we define
Here on the right we take the Chern character of coherent
![]() $\mathcal{O}_X$
-modules. Equivalently (via Proposition 2.18), if
$\mathcal{O}_X$
-modules. Equivalently (via Proposition 2.18), if
![]() $\pi : Y \to X$
is the Brauer–Severi variety corresponding to
$\pi : Y \to X$
is the Brauer–Severi variety corresponding to
![]() $\mathcal{A} = \pi _*(\mathcal{E}{\textit{nd}(G^\vee )})$
and
$\mathcal{A} = \pi _*(\mathcal{E}{\textit{nd}(G^\vee )})$
and
![]() $F$
is a
$F$
is a
![]() $Y$
-sheaf, we define
$Y$
-sheaf, we define
where
![]() $G$
is the sheaf defined in Lemma 2.4. We view these Chern characters as elements of
$G$
is the sheaf defined in Lemma 2.4. We view these Chern characters as elements of
![]() $H^*(X,\mathbb{Q})$
. The component of
$H^*(X,\mathbb{Q})$
. The component of
![]() ${{\rm ch}}_G(F)$
in
${{\rm ch}}_G(F)$
in
![]() $H^0(X,\mathbb{Z})$
equals
$H^0(X,\mathbb{Z})$
equals
![]() ${{\rm rk}}(F)$
.
${{\rm rk}}(F)$
.
We refer to the factor
![]() $e^{\xi /r}$
as the Huybrechts–Stellari twist introduced in [Reference Huybrechts and StellariHS05]. The class
$e^{\xi /r}$
as the Huybrechts–Stellari twist introduced in [Reference Huybrechts and StellariHS05]. The class
![]() $\xi /r \in H^2(X,\mathbb{Q})$
is called a rational
$\xi /r \in H^2(X,\mathbb{Q})$
is called a rational
![]() $B$
-field. The Huybrechts–Stellari twist has the desirable feature that
$B$
-field. The Huybrechts–Stellari twist has the desirable feature that
![]() ${\rm ch}^\xi _{\mathcal{A}}(F)$
has the following integrality property shown in [Reference YoshiokaYos06] for K3 surfaces (but it holds for arbitrary surfaces with
${\rm ch}^\xi _{\mathcal{A}}(F)$
has the following integrality property shown in [Reference YoshiokaYos06] for K3 surfaces (but it holds for arbitrary surfaces with
![]() $H_1(X,\mathbb{Z})$
torsion free [Reference Jiang and KoolJK21]).
$H_1(X,\mathbb{Z})$
torsion free [Reference Jiang and KoolJK21]).
Proposition 3.3.
Let
![]() $\mathcal{A}$
be an Azumaya algebra on a surface
$\mathcal{A}$
be an Azumaya algebra on a surface
![]() $X$
. For any left
$X$
. For any left
![]() $\mathcal{A}$
-module
$\mathcal{A}$
-module
![]() $F$
, choose a representing element
$F$
, choose a representing element
![]() $\xi$
for
$\xi$
for
![]() $w(\mathcal{A}) \in H^2(X,\mu _r)$
and write
$w(\mathcal{A}) \in H^2(X,\mu _r)$
and write
Then
![]() $c_1 \in H^2(X,\mathbb{Z})$
and
$c_1 \in H^2(X,\mathbb{Z})$
and
![]() $c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
.
$c_2 \in H^4(X,\mathbb{Z}) \cong \mathbb{Z}$
.
We wish to provide more motivation for Definition 3.2. Suppose that
![]() $\mathcal{A} = \mathcal{E}{\textit{nd}}(E^\vee )$
is a trivial Azumaya algebra. Then every left
$\mathcal{A} = \mathcal{E}{\textit{nd}}(E^\vee )$
is a trivial Azumaya algebra. Then every left
![]() $\mathcal{A}$
-module
$\mathcal{A}$
-module
![]() $M$
is of the form
$M$
is of the form
![]() $F \otimes E^\vee$
for
$F \otimes E^\vee$
for
![]() $F$
a coherent sheaf on
$F$
a coherent sheaf on
![]() $X$
by Example 2.25. One might expect that
$X$
by Example 2.25. One might expect that
![]() ${{\rm ch}}_{\mathcal{A}}^{\xi }(M) ={{\rm ch}}(F)$
. And indeed, this can be verified: on a surface
${{\rm ch}}_{\mathcal{A}}^{\xi }(M) ={{\rm ch}}(F)$
. And indeed, this can be verified: on a surface
![]() $X$
, we have
$X$
, we have
Keeping in mind that
![]() $\xi = c_1(E)$
represents
$\xi = c_1(E)$
represents
![]() $w$
, see (6), we can rewrite this as
$w$
, see (6), we can rewrite this as
There is an alternative perspective. We can view our surface as a complex manifold and forget the complex structure; what remains is a topological space. There is a notion of topological Azumaya algebras on this space. Their classes take values in the topological Brauer group, which is the torsion part of
![]() $H^3(X, \mathbb{Z})$
, which is zero in our case because we assume
$H^3(X, \mathbb{Z})$
, which is zero in our case because we assume
![]() $H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
. Hence, any topological Azumaya algebra is trivialized by a topological vector bundle, and this vector bundle is unique up to tensoring by a topological line bundle (that is, a class in
$H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
. Hence, any topological Azumaya algebra is trivialized by a topological vector bundle, and this vector bundle is unique up to tensoring by a topological line bundle (that is, a class in
![]() $H^2(X, \mathbb{Z})$
). One can use this to define Chern classes, and a similar calculation shows that they are the same as the previous definition. For details on topological Azumaya algebras, we refer the reader to [Reference Antieau and WilliamsAW13]. Similar ideas to what we have described also appear in [Reference HeinlothHei05, Reference YoshiokaYos06].
$H^2(X, \mathbb{Z})$
). One can use this to define Chern classes, and a similar calculation shows that they are the same as the previous definition. For details on topological Azumaya algebras, we refer the reader to [Reference Antieau and WilliamsAW13]. Similar ideas to what we have described also appear in [Reference HeinlothHei05, Reference YoshiokaYos06].
3.2 Moduli spaces
Let
![]() $(X,H)$
be a smooth polarized surface and suppose
$(X,H)$
be a smooth polarized surface and suppose
![]() $H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
. Let
$H_1(X,\mathbb{Z})_{{\rm tor}} = 0$
. Let
![]() $\pi : Y \to X$
be a Brauer–Severi variety of degree
$\pi : Y \to X$
be a Brauer–Severi variety of degree
![]() $r$
with corresponding Azumaya algebra
$r$
with corresponding Azumaya algebra
![]() $\mathcal{A}$
. On the one hand, one can consider moduli spaces of stable
$\mathcal{A}$
. On the one hand, one can consider moduli spaces of stable
![]() $Y$
-sheaves on
$Y$
-sheaves on
![]() $X$
constructed by Yoshioka [Reference YoshiokaYos06]. On the other hand, one can consider moduli spaces of generically simple torsion free left
$X$
constructed by Yoshioka [Reference YoshiokaYos06]. On the other hand, one can consider moduli spaces of generically simple torsion free left
![]() $\mathcal{A}$
-modules constructed by Hoffmann and Stuhler [Reference Hoffmann and StuhlerHS05]. We recall the main results on these moduli spaces. Since
$\mathcal{A}$
-modules constructed by Hoffmann and Stuhler [Reference Hoffmann and StuhlerHS05]. We recall the main results on these moduli spaces. Since
![]() ${\rm Coh}(X,Y)$
and
${\rm Coh}(X,Y)$
and
![]() ${\rm Coh}(X,\mathcal{A})$
are equivalent, one expects these moduli spaces to be isomorphic as was shown by Reede [Reference ReedeRee18].
${\rm Coh}(X,\mathcal{A})$
are equivalent, one expects these moduli spaces to be isomorphic as was shown by Reede [Reference ReedeRee18].
We first recall Yoshioka’s result [Reference YoshiokaYos06]. Let
![]() $G$
be the unique (up to scaling) non-trivial extension of
$G$
be the unique (up to scaling) non-trivial extension of
![]() $T_{Y/X}$
by
$T_{Y/X}$
by
![]() $\mathcal{O}_Y$
of Lemma 2.4. For a
$\mathcal{O}_Y$
of Lemma 2.4. For a
![]() $Y$
-sheaf
$Y$
-sheaf
![]() $F$
, its twisted Hilbert polynomial is defined by [Reference YoshiokaYos06]
$F$
, its twisted Hilbert polynomial is defined by [Reference YoshiokaYos06]
Suppose
![]() $F$
is torsion free. Then the above polynomial has degree 2 and we denote its leading term by
$F$
is torsion free. Then the above polynomial has degree 2 and we denote its leading term by
![]() ${1 \over 2}a_2^G(F) m^2$
. One defines
${1 \over 2}a_2^G(F) m^2$
. One defines
![]() $F$
as semistable (with respect to
$F$
as semistable (with respect to
![]() $H$
) if
$H$
) if
for all
![]() $Y$
-subsheaves
$Y$
-subsheaves
![]() $0 \neq F^{\prime} \subsetneq F$
. Stability is defined analogously with
$0 \neq F^{\prime} \subsetneq F$
. Stability is defined analogously with
![]() $\leq$
replaced by
$\leq$
replaced by
![]() $\lt$
.
$\lt$
.
Definition 3.4. For any choice of Chern character
![]() ${\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
, Yoshioka proves there exists a coarse moduli space
${\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
, Yoshioka proves there exists a coarse moduli space
![]() $M_Y^{H,ss}({\rm ch})$
parametrizing
$M_Y^{H,ss}({\rm ch})$
parametrizing
![]() $S$
-equivalence classes of semistable
$S$
-equivalence classes of semistable
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $F$
with
$F$
with
![]() ${\rm ch}_G(F) = {\rm ch}$
. Moreover,
${\rm ch}_G(F) = {\rm ch}$
. Moreover,
![]() $M_Y^{H,ss}({\rm ch})$
is a projective scheme. Furthermore,
$M_Y^{H,ss}({\rm ch})$
is a projective scheme. Furthermore,
![]() $M_Y^{H,ss}({\rm ch})$
contains an open subscheme
$M_Y^{H,ss}({\rm ch})$
contains an open subscheme
![]() $M_Y^H({\rm ch})$
parametrizing isomorphism classes of stable
$M_Y^H({\rm ch})$
parametrizing isomorphism classes of stable
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $F$
on
$F$
on
![]() $X$
with
$X$
with
![]() ${\rm ch}_G(F) = {\rm ch}$
.
${\rm ch}_G(F) = {\rm ch}$
.
We sometimes prefer fixing Chern classes instead of Chern characters, in which case we write
![]() $M_Y^{H,ss}(s,c_1,c_2)$
and
$M_Y^{H,ss}(s,c_1,c_2)$
and
![]() $M_Y^{H}(s,c_1,c_2)$
. Representing the Stiefel–Whitney class
$M_Y^{H}(s,c_1,c_2)$
. Representing the Stiefel–Whitney class
![]() $w(Y)$
by
$w(Y)$
by
![]() $\xi \in H^2(X,\mu _r)$
, we sometimes prefer to fix
$\xi \in H^2(X,\mu _r)$
, we sometimes prefer to fix
![]() ${\rm ch}_G^\xi (F) = {\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2)$
, in which case we denote the corresponding moduli spaces by
${\rm ch}_G^\xi (F) = {\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2)$
, in which case we denote the corresponding moduli spaces by
Then we have
![]() $s \in \mathbb{Z}$
,
$s \in \mathbb{Z}$
,
![]() $c_1 \in H^2(X,\mathbb{Z})$
, and
$c_1 \in H^2(X,\mathbb{Z})$
, and
![]() $c_2 \in \mathbb{Z}$
(Proposition 3.3).
$c_2 \in \mathbb{Z}$
(Proposition 3.3).
Remark 3.5. Suppose we take
![]() $s$
equal to the order of
$s$
equal to the order of
![]() $\alpha (Y) \in {\rm Br}(X)$
. Then
$\alpha (Y) \in {\rm Br}(X)$
. Then
![]() $s$
is the minimal rank among all (coherent)
$s$
is the minimal rank among all (coherent)
![]() $Y$
-sheaves of positive rank [Reference YoshiokaYos06, Lemma 3.2, Remark 3.1]. This implies all rank
$Y$
-sheaves of positive rank [Reference YoshiokaYos06, Lemma 3.2, Remark 3.1]. This implies all rank
![]() $s$
torsion free
$s$
torsion free
![]() $Y$
-sheaves are automatically stable and semistable! This is a crucial feature of the theory of twisted sheaves.
$Y$
-sheaves are automatically stable and semistable! This is a crucial feature of the theory of twisted sheaves.
We now recall Hoffmann and Stuhler’s result. They consider left
![]() $\mathcal{A}$
-modules
$\mathcal{A}$
-modules
![]() $F$
which are torsion free (as
$F$
which are torsion free (as
![]() $\mathcal{O}_X$
-module) and generically simple, i.e. over the generic point
$\mathcal{O}_X$
-module) and generically simple, i.e. over the generic point
![]() $\eta \in X$
the
$\eta \in X$
the
![]() $\mathcal{A}_\eta$
-module
$\mathcal{A}_\eta$
-module
![]() $F_\eta$
is simple. By Wedderburn’s theorem, over the generic point
$F_\eta$
is simple. By Wedderburn’s theorem, over the generic point
![]() $\mathcal{A}_\eta \cong M_n(D)$
for some division algebra
$\mathcal{A}_\eta \cong M_n(D)$
for some division algebra
![]() $D$
over
$D$
over
![]() $\mathbb{C}(X)$
and some
$\mathbb{C}(X)$
and some
![]() $n \in \mathbb{Z}_{\gt 0}$
, and simplicity means
$n \in \mathbb{Z}_{\gt 0}$
, and simplicity means
![]() $F_\eta \cong D^{\oplus n}$
(with
$F_\eta \cong D^{\oplus n}$
(with
![]() $\mathcal{A}_\eta$
-module structure induced by matrix multiplication). One crucial observation is that the algebra of
$\mathcal{A}_\eta$
-module structure induced by matrix multiplication). One crucial observation is that the algebra of
![]() $\mathcal{A}$
-endomorphisms
$\mathcal{A}$
-endomorphisms
![]() ${{\rm End}} _{\mathcal{A}}(F)$
is a finite-dimensional
${{\rm End}} _{\mathcal{A}}(F)$
is a finite-dimensional
![]() $\mathbb{C}$
-algebra, which is moreover a division ring because we have an embedding [Reference Hoffmann and StuhlerHS05]
$\mathbb{C}$
-algebra, which is moreover a division ring because we have an embedding [Reference Hoffmann and StuhlerHS05]
hence
![]() ${{\rm End}} _{\mathcal{A}}(F) = \mathbb{C}$
. Therefore, we do not have non-trivial automorphisms. In fact, no notion of stability is required.
${{\rm End}} _{\mathcal{A}}(F) = \mathbb{C}$
. Therefore, we do not have non-trivial automorphisms. In fact, no notion of stability is required.
Definition 3.6. For any choice of Chern character
![]() ${\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
, Hoffmann and Stuhler prove there exists a coarse moduli space
${\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
, Hoffmann and Stuhler prove there exists a coarse moduli space
![]() $M_{\mathcal{A}}({\rm ch})$
parametrizing isomorphism classes of generically simple torsion free left
$M_{\mathcal{A}}({\rm ch})$
parametrizing isomorphism classes of generically simple torsion free left
![]() $\mathcal{A}$
-modules
$\mathcal{A}$
-modules
![]() $F$
with
$F$
with
![]() ${\rm ch}_{\mathcal{A}}(F) = {\rm ch}$
. Moreover,
${\rm ch}_{\mathcal{A}}(F) = {\rm ch}$
. Moreover,
![]() $M_{\mathcal{A}}({\rm ch})$
is a projective scheme.
$M_{\mathcal{A}}({\rm ch})$
is a projective scheme.
The property of generic simplicity implies
![]() $s = {\rm deg}(D) := \sqrt{{\rm dim}_{\mathbb{C}(X)}(D)}$
(and in particular
$s = {\rm deg}(D) := \sqrt{{\rm dim}_{\mathbb{C}(X)}(D)}$
(and in particular
![]() $F$
has rank
$F$
has rank
![]() $ns^2$
as
$ns^2$
as
![]() $\mathcal{O}_X$
-module). Therefore, we may suppress rank
$\mathcal{O}_X$
-module). Therefore, we may suppress rank
![]() $s$
from the notation. Also recall that
$s$
from the notation. Also recall that
![]() $\mathcal{A}$
has degree
$\mathcal{A}$
has degree
![]() $r$
, so
$r$
, so
![]() $r,n,s$
are related by
$r,n,s$
are related by
![]() $r = ns$
. We sometimes prefer fixing Chern classes instead of Chern characters, in which case we write
$r = ns$
. We sometimes prefer fixing Chern classes instead of Chern characters, in which case we write
![]() $M_{\mathcal{A}}(c_1,c_2)$
. Moreover, sometimes we fix the twisted Chern character
$M_{\mathcal{A}}(c_1,c_2)$
. Moreover, sometimes we fix the twisted Chern character
![]() ${\rm ch}^\xi _{\mathcal{A}}(F) = {\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2)$
, in which case we denote the corresponding moduli space by
${\rm ch}^\xi _{\mathcal{A}}(F) = {\rm ch} = (s, c_1, {1 \over 2} c_1^2 - c_2)$
, in which case we denote the corresponding moduli space by
In the setting of Azumaya algebras, one often only considers the case
![]() $n=1$
, i.e.
$n=1$
, i.e.
![]() $\mathcal{A}_\eta \cong D$
. The reason is that one can replace
$\mathcal{A}_\eta \cong D$
. The reason is that one can replace
![]() $\mathcal{A}$
by a Brauer equivalent Azumaya algebra with this property [Reference ReedeRee18, Remark 2.1] and replacing
$\mathcal{A}$
by a Brauer equivalent Azumaya algebra with this property [Reference ReedeRee18, Remark 2.1] and replacing
![]() $\mathcal{A}$
by a Brauer equivalent Azumaya algebra does not change the category of left modules (Example 2.25).
$\mathcal{A}$
by a Brauer equivalent Azumaya algebra does not change the category of left modules (Example 2.25).
Then the degree
![]() $r$
of the Azumaya algebra
$r$
of the Azumaya algebra
![]() $\mathcal{A}$
is equal to its index which is defined as the degree of
$\mathcal{A}$
is equal to its index which is defined as the degree of
![]() $D$
. By the period-index theorem [Reference de JongdJo04], this is also the period of
$D$
. By the period-index theorem [Reference de JongdJo04], this is also the period of
![]() $\mathcal{A}$
which is defined as the order of the Brauer class
$\mathcal{A}$
which is defined as the order of the Brauer class
![]() $\alpha (\mathcal{A})$
.Footnote
11
For
$\alpha (\mathcal{A})$
.Footnote
11
For
![]() $n=1$
, we have the following result.
$n=1$
, we have the following result.
Theorem 3.7. (Reede). The equivalence of categories of Proposition 2.18 induces an isomorphism of moduli spaces
In particular, all rank
![]() $r$
torsion free
$r$
torsion free
![]() $Y$
-sheaves are automatically stable and the space
$Y$
-sheaves are automatically stable and the space
![]() $M_{Y}^{H}(r,c_1,c_2)$
is projective and independent of
$M_{Y}^{H}(r,c_1,c_2)$
is projective and independent of
![]() $H$
.
$H$
.
In fact, Reede identifies the moduli functors, not just the coarse spaces.
Still working under the assumption
![]() $\mathcal{A}_\eta \cong D$
, Hoffmann and Stuhler consider the locus
$\mathcal{A}_\eta \cong D$
, Hoffmann and Stuhler consider the locus
of locally free
![]() $\mathcal{A}$
-modules of rank 1 (as
$\mathcal{A}$
-modules of rank 1 (as
![]() $\mathcal{A}$
-modules). Note that
$\mathcal{A}$
-modules). Note that
![]() ${\rm Pic}(X)$
acts on the union of these moduli spaces over all
${\rm Pic}(X)$
acts on the union of these moduli spaces over all
![]() $c_1, c_2$
by
$c_1, c_2$
by
![]() $F \mapsto F \otimes L$
.
$F \mapsto F \otimes L$
.
Proposition 3.8. (Hoffmann–Stuhler). The map
![]() $F \to \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)^{{\rm op}}$
gives a bijection between the closed points of
$F \to \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)^{{\rm op}}$
gives a bijection between the closed points of
and the set of isomorphism classes of Azumaya algebras
![]() $\mathcal{B}$
on
$\mathcal{B}$
on
![]() $X$
satisfying
$X$
satisfying
![]() $\mathcal{B}_\eta \cong D$
. Under this bijection
$\mathcal{B}_\eta \cong D$
. Under this bijection
![]() $c_2(\mathcal{B}) =2rc_2 - (r-1) c_1^2$
.
$c_2(\mathcal{B}) =2rc_2 - (r-1) c_1^2$
.
Proof.
This is [Reference Hoffmann and StuhlerHS05, Proposition 4.1], except for the calculation of
![]() $c_2(\mathcal{B})$
with
$c_2(\mathcal{B})$
with
![]() $\mathcal{B} = \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)^{{\rm op}}$
where
$\mathcal{B} = \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)^{{\rm op}}$
where
![]() $F$
is a locally free
$F$
is a locally free
![]() $\mathcal{A}$
-modules of rank 1 (as
$\mathcal{A}$
-modules of rank 1 (as
![]() $\mathcal{A}$
-module). The natural map
$\mathcal{A}$
-module). The natural map
is an isomorphism. Since
![]() $c_1(\mathcal{A}) = 0$
, we obtain
$c_1(\mathcal{A}) = 0$
, we obtain
 \begin{align}{{\rm ch}}(\mathcal{B}) ={{\rm ch}}(\mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)) = {{{\rm ch}}(\mathcal{E}{\textit{nd}}(F)) \over {{\rm ch}}(\mathcal{A})} = {{{\rm ch}}(F) \over \sqrt{{{\rm ch}}(\mathcal{A})}} \Bigg ( {{{\rm ch}}(F) \over \sqrt{{{\rm ch}}(\mathcal{A}})} \Bigg )^\vee = r^2 + (r-1)c_1^2 -2rc_2, \end{align}
\begin{align}{{\rm ch}}(\mathcal{B}) ={{\rm ch}}(\mathcal{E}{\textit{nd}}_{\mathcal{A}}(F)) = {{{\rm ch}}(\mathcal{E}{\textit{nd}}(F)) \over {{\rm ch}}(\mathcal{A})} = {{{\rm ch}}(F) \over \sqrt{{{\rm ch}}(\mathcal{A})}} \Bigg ( {{{\rm ch}}(F) \over \sqrt{{{\rm ch}}(\mathcal{A}})} \Bigg )^\vee = r^2 + (r-1)c_1^2 -2rc_2, \end{align}
from which the result follows.
Corollary 3.9.
If
![]() $M_{\mathcal{A}}(c_1,c_2) \neq \varnothing$
, then there exists an Azumaya algebra
$M_{\mathcal{A}}(c_1,c_2) \neq \varnothing$
, then there exists an Azumaya algebra
![]() $\mathcal{B}$
on
$\mathcal{B}$
on
![]() $X$
satisfying
$X$
satisfying
![]() $\mathcal{B}_\eta \cong D$
and
$\mathcal{B}_\eta \cong D$
and
Proof.
Taking an element
![]() $F$
in
$F$
in
![]() $M_{\mathcal{A}}(c_1,c_2)$
, its double dual (as
$M_{\mathcal{A}}(c_1,c_2)$
, its double dual (as
![]() $\mathcal{O}_X$
-module)
$\mathcal{O}_X$
-module)
![]() $F^{**} = \mathcal{H}{\textit{om}}(\mathcal{H}{\textit{om}}(F,\mathcal{O}_X),\mathcal{O}_X)$
has a natural left
$F^{**} = \mathcal{H}{\textit{om}}(\mathcal{H}{\textit{om}}(F,\mathcal{O}_X),\mathcal{O}_X)$
has a natural left
![]() $\mathcal{A}$
-module structure and is locally free (as
$\mathcal{A}$
-module structure and is locally free (as
![]() $\mathcal{O}_X$
-module). Consider the short exact sequence of
$\mathcal{O}_X$
-module). Consider the short exact sequence of
![]() $\mathcal{O}_X$
-modules
$\mathcal{O}_X$
-modules
induced by the natural inclusion
![]() $F \hookrightarrow F^{**}$
. Then
$F \hookrightarrow F^{**}$
. Then
![]() $Q$
is 0-dimensional, so
$Q$
is 0-dimensional, so
![]() ${{\rm rk}}(F^{**}) ={{\rm rk}}(F) = r^2$
(implying
${{\rm rk}}(F^{**}) ={{\rm rk}}(F) = r^2$
(implying
![]() $F^{**}$
is locally free of rank 1 as
$F^{**}$
is locally free of rank 1 as
![]() $\mathcal{A}$
-module by Proposition 2.21),
$\mathcal{A}$
-module by Proposition 2.21),
![]() $c_1(F^{**}) = c_1(F)$
, and
$c_1(F^{**}) = c_1(F)$
, and
![]() $c_2(F^{**}) = c_2(F) + c_2(Q) \leq c_2(F)$
. Taking
$c_2(F^{**}) = c_2(F) + c_2(Q) \leq c_2(F)$
. Taking
![]() $\mathcal{B} = \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F^{**})^{{\rm op}}$
, the result follows from Proposition 3.8.
$\mathcal{B} = \mathcal{E}{\textit{nd}}_{\mathcal{A}}(F^{**})^{{\rm op}}$
, the result follows from Proposition 3.8.
Remark 3.10. In the previous proposition and corollary, we can also replace
![]() $M_{\mathcal{A}}^{{\rm lf}}(c_1,c_2)$
by
$M_{\mathcal{A}}^{{\rm lf}}(c_1,c_2)$
by
![]() $M_{\mathcal{A},\xi /r}^{{\rm lf}}(c_1,c_2)$
, i.e. we fix Chern character twisted by the
$M_{\mathcal{A},\xi /r}^{{\rm lf}}(c_1,c_2)$
, i.e. we fix Chern character twisted by the
![]() $B$
-field, and obtain the same conclusions.
$B$
-field, and obtain the same conclusions.
In § 5.3, we present a method to detect the condition ‘
![]() $M_{\mathcal{A}}(c_1,c_2) \neq \varnothing$
’ by showing that certain intersection numbers on the moduli space are non-zero.
$M_{\mathcal{A}}(c_1,c_2) \neq \varnothing$
’ by showing that certain intersection numbers on the moduli space are non-zero.
Remark 3.11. Suppose
![]() $H_1(X,\mathbb{Z}) = 0$
. Lieblich has shown that there exists a (sufficiently large) second Chern class
$H_1(X,\mathbb{Z}) = 0$
. Lieblich has shown that there exists a (sufficiently large) second Chern class
![]() $c_2 \in \mathbb{Q}$
such that
$c_2 \in \mathbb{Q}$
such that
![]() $M_{\mathcal{A}}^{{\rm lf}}(0,c_2+k) \neq \varnothing$
for all
$M_{\mathcal{A}}^{{\rm lf}}(0,c_2+k) \neq \varnothing$
for all
![]() $k \in \mathbb{Z}_{\geq 0}$
[Reference LieblichLie09, Theormm 6.2.4]. More precisely, let
$k \in \mathbb{Z}_{\geq 0}$
[Reference LieblichLie09, Theormm 6.2.4]. More precisely, let
![]() $\mathcal{G} := w(\mathcal{A}) \in H^2(X,\mu _r)$
be the optimal
$\mathcal{G} := w(\mathcal{A}) \in H^2(X,\mu _r)$
be the optimal
![]() $\mu _r$
-gerbe corresponding to
$\mu _r$
-gerbe corresponding to
![]() $\mathcal{A}$
and let
$\mathcal{A}$
and let
![]() $\pi : \mathcal{G} \to X$
be the map to the coarse moduli space. For this remark, fix a Chern character
$\pi : \mathcal{G} \to X$
be the map to the coarse moduli space. For this remark, fix a Chern character
![]() ${{\rm ch}}_{\mathcal{A}} := (r,c_1,\tfrac{1}{2} c_1^2 - c_2)$
in the Chow group
${{\rm ch}}_{\mathcal{A}} := (r,c_1,\tfrac{1}{2} c_1^2 - c_2)$
in the Chow group
![]() $A^*(X)_{\mathbb{Q}}$
. Moreover, let
$A^*(X)_{\mathbb{Q}}$
. Moreover, let
![]() $\pi ^*{{\rm ch}}_{\mathcal{A}} =: {\rm ch}^{\prime} = (r,c_1^{\prime},\tfrac{1}{2} c_1^{\prime 2} - c_2^{\prime})$
in
$\pi ^*{{\rm ch}}_{\mathcal{A}} =: {\rm ch}^{\prime} = (r,c_1^{\prime},\tfrac{1}{2} c_1^{\prime 2} - c_2^{\prime})$
in
![]() $A^*(\mathcal{G})_{\mathbb{Q}}$
. Denote by
$A^*(\mathcal{G})_{\mathbb{Q}}$
. Denote by
![]() ${\bf Tw}_{\mathcal{G}}(r,c_1^{\prime},c_2^{\prime})$
Lieblich’s moduli stack of torsion free twisted sheaves
${\bf Tw}_{\mathcal{G}}(r,c_1^{\prime},c_2^{\prime})$
Lieblich’s moduli stack of torsion free twisted sheaves
![]() $F$
on
$F$
on
![]() $\mathcal{G}$
with
$\mathcal{G}$
with
![]() ${{\rm ch}}(F) = {\rm ch}^{\prime}$
. Recall that
${{\rm ch}}(F) = {\rm ch}^{\prime}$
. Recall that
![]() $ \mathcal{A}|_{\mathcal{G}} \cong \mathcal{E}{\textit{nd}}(E^\vee )$
for some locally free twisted sheaf
$ \mathcal{A}|_{\mathcal{G}} \cong \mathcal{E}{\textit{nd}}(E^\vee )$
for some locally free twisted sheaf
![]() $E$
of rank
$E$
of rank
![]() $r$
on
$r$
on
![]() $\mathcal{G}$
, which we can choose to satisfy
$\mathcal{G}$
, which we can choose to satisfy
![]() $c_1(E)=0$
(Example 2.14). It is not hard to see that the equivalence of Proposition 2.21 induces a bijection between (isomorphism classes of) the
$c_1(E)=0$
(Example 2.14). It is not hard to see that the equivalence of Proposition 2.21 induces a bijection between (isomorphism classes of) the
![]() $\mathbb{C}$
-valued points of
$\mathbb{C}$
-valued points of
![]() ${\bf Tw}_{\mathcal{G}}(r,c_1^{\prime},c_2^{\prime})$
and
${\bf Tw}_{\mathcal{G}}(r,c_1^{\prime},c_2^{\prime})$
and
![]() $M_{\mathcal{A}}(c_1,c_2)$
.Footnote
12
The bijection also preserves locally free objects.
$M_{\mathcal{A}}(c_1,c_2)$
.Footnote
12
The bijection also preserves locally free objects.
Now take
![]() $c_1 = c_1^{\prime}=0$
. By the existence of
$c_1 = c_1^{\prime}=0$
. By the existence of
![]() $E$
, at least one of the stacks
$E$
, at least one of the stacks
![]() ${\bf Tw}_{\mathcal{G}}(r,0,c_2^{\prime})$
has a locally free object. Moreover, Lieblich shows that if
${\bf Tw}_{\mathcal{G}}(r,0,c_2^{\prime})$
has a locally free object. Moreover, Lieblich shows that if
![]() $\Delta ^{\prime}:=2rc_2^{\prime} - (r-1)c_1^{\prime 2} = r^{-1}(2rc_2 - (r-1)c_1^2)=2rc_2^{\prime} = 2c_2$
is sufficiently large, then
$\Delta ^{\prime}:=2rc_2^{\prime} - (r-1)c_1^{\prime 2} = r^{-1}(2rc_2 - (r-1)c_1^2)=2rc_2^{\prime} = 2c_2$
is sufficiently large, then
![]() ${\bf Tw}_{\mathcal{G}}(r,0,c_2^{\prime} + k/r)$
has a locally free object for all
${\bf Tw}_{\mathcal{G}}(r,0,c_2^{\prime} + k/r)$
has a locally free object for all
![]() $k \in \mathbb{Z}_{\geq 0}$
[Reference LieblichLie09, Theoremm 6.2.4].Footnote
13
Hence, there exists a Chern class
$k \in \mathbb{Z}_{\geq 0}$
[Reference LieblichLie09, Theoremm 6.2.4].Footnote
13
Hence, there exists a Chern class
![]() $c_2$
such that
$c_2$
such that
![]() $M_{\mathcal{A}}^{{\rm lf}}(0,c_2+k) \neq \varnothing$
for all
$M_{\mathcal{A}}^{{\rm lf}}(0,c_2+k) \neq \varnothing$
for all
![]() $k \in \mathbb{Z}_{\geq 0}$
. However, there is no a priori control over the value of
$k \in \mathbb{Z}_{\geq 0}$
. However, there is no a priori control over the value of
![]() $c_2$
. Instead, our goal is to find values of
$c_2$
. Instead, our goal is to find values of
![]() $c_2$
, with explicit lower and upper bound, for which
$c_2$
, with explicit lower and upper bound, for which
![]() $M_{\mathcal{A}}(0,c_2) \neq \varnothing$
.
$M_{\mathcal{A}}(0,c_2) \neq \varnothing$
.
4. Invariants of moduli of twisted sheaves
4.1 Obstruction theory
Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
. Let
$H_1(X,\mathbb{Z}) = 0$
. Let
![]() $Y \to X$
be a Brauer–Severi variety of degree
$Y \to X$
be a Brauer–Severi variety of degree
![]() $r$
and consider the moduli spaces
$r$
and consider the moduli spaces
![]() $M:=M_{Y}^{H}({\rm ch})$
of the previous section.Footnote
14
Denote by
$M:=M_{Y}^{H}({\rm ch})$
of the previous section.Footnote
14
Denote by
![]() $\pi _M : Y \times M \rightarrow M$
the projection. Although a universal sheaf
$\pi _M : Y \times M \rightarrow M$
the projection. Although a universal sheaf
![]() $\mathcal{E}$
may not exist globally on
$\mathcal{E}$
may not exist globally on
![]() $Y \times M$
, the complex
$Y \times M$
, the complex
exists globally on
![]() $Y \times M$
[Reference CăldăraruCal00, Reference Huybrechts and LehnHL10]. Put differently,
$Y \times M$
[Reference CăldăraruCal00, Reference Huybrechts and LehnHL10]. Put differently,
![]() $\mathcal{E}$
exists as a twisted sheaf on
$\mathcal{E}$
exists as a twisted sheaf on
![]() $Y \times M$
. Denote the truncated cotangent complex of
$Y \times M$
. Denote the truncated cotangent complex of
![]() $M$
by
$M$
by
![]() $\mathbb{L}_M = \tau ^{\geq -1} L_M$
. The following result is well known in the untwisted case [Reference Huybrechts and ThomasHT09] and shown in the twisted case in [Reference Jiang and KoolJK21].
$\mathbb{L}_M = \tau ^{\geq -1} L_M$
. The following result is well known in the untwisted case [Reference Huybrechts and ThomasHT09] and shown in the twisted case in [Reference Jiang and KoolJK21].
Proposition 4.1.
Fix
![]() ${{\rm ch}} = (s,c_1,{1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
. Then the moduli space
${{\rm ch}} = (s,c_1,{1 \over 2} c_1^2 - c_2) \in H^*(X,\mathbb{Q})$
. Then the moduli space
![]() $M:=M_{Y}^{H}({\rm ch})$
has a perfect obstruction theory
$M:=M_{Y}^{H}({\rm ch})$
has a perfect obstruction theory
of virtual dimension
By the work of Behrend and Fantechi [Reference Behrend and FantechiBF97], we therefore obtain a virtual fundamental class of degree
![]() ${\rm vd}(s,c_1,c_2)$
in the Chow group of
${\rm vd}(s,c_1,c_2)$
in the Chow group of
![]() $M$
$M$
We provide the following two additional perspectives on this obstruction theory.
Remark 4.2. Let
![]() $\mathcal{G} \to X$
be the
$\mathcal{G} \to X$
be the
![]() $\mu _r$
-gerbe corresponding to
$\mu _r$
-gerbe corresponding to
![]() $w(Y) \in H^2(X,\mu _r)$
. Then the analogue of this proposition was shown for the moduli stack
$w(Y) \in H^2(X,\mu _r)$
. Then the analogue of this proposition was shown for the moduli stack
![]() ${\bf Tw}_{\mathcal{G}}^{s}(r,0,c_2)$
of twisted sheaves on
${\bf Tw}_{\mathcal{G}}^{s}(r,0,c_2)$
of twisted sheaves on
![]() $\mathcal{G}$
by Lieblich [Reference LieblichLie09, Proposition 6.5.1.1]. Another way to view this proposition is as follows. Let
$\mathcal{G}$
by Lieblich [Reference LieblichLie09, Proposition 6.5.1.1]. Another way to view this proposition is as follows. Let
![]() $\boldsymbol{M}$
be the derived stack of simple sheaves with fixed determinant on
$\boldsymbol{M}$
be the derived stack of simple sheaves with fixed determinant on
![]() $Y$
. Then its classical truncation
$Y$
. Then its classical truncation
![]() $M^{{\rm cl}}$
has an obstruction theory
$M^{{\rm cl}}$
has an obstruction theory
Yoshioka proved that the locus of
![]() $Y$
-sheaves is open in
$Y$
-sheaves is open in
![]() $M^{{\rm cl}}$
[Reference YoshiokaYos06, Lemma 1.6.5], so we can restrict
$M^{{\rm cl}}$
[Reference YoshiokaYos06, Lemma 1.6.5], so we can restrict
![]() $\mathbb{E} \to L_{M^{{\rm cl}}}$
to this open locus (alhough we are now on a stack, which is a
$\mathbb{E} \to L_{M^{{\rm cl}}}$
to this open locus (alhough we are now on a stack, which is a
![]() $\mathbb{G}_m$
-gerbe over the moduli scheme in Proposition 4.1).
$\mathbb{G}_m$
-gerbe over the moduli scheme in Proposition 4.1).
We are interested in the relative situation. Suppose
![]() $f : \mathcal{X} \to B$
is a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
$f : \mathcal{X} \to B$
is a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
![]() $B$
. We assume that one fibre (and hence all fibres)
$B$
. We assume that one fibre (and hence all fibres)
![]() $\mathcal{X}_b$
satisfies
$\mathcal{X}_b$
satisfies
![]() $H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. Suppose
$H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. Suppose
![]() $\pi : \mathcal{Y} \to \mathcal{X}$
is a smooth projective morphism of relative dimension
$\pi : \mathcal{Y} \to \mathcal{X}$
is a smooth projective morphism of relative dimension
![]() $r-1$
such that the fibres over closed points
$r-1$
such that the fibres over closed points
![]() $b \in B$
are Brauer–Severi varieties
$b \in B$
are Brauer–Severi varieties
![]() $\mathcal{Y}_b \to \mathcal{X}_b$
. Moreover, we denote by
$\mathcal{Y}_b \to \mathcal{X}_b$
. Moreover, we denote by
![]() $G_b$
the unique (up to scaling) non-trivial extension of
$G_b$
the unique (up to scaling) non-trivial extension of
![]() $T_{\mathcal{Y}_b/\mathcal{X}_b}$
by
$T_{\mathcal{Y}_b/\mathcal{X}_b}$
by
![]() $\mathcal{O}_{\mathcal{Y}_b}$
(Lemma 2.4).
$\mathcal{O}_{\mathcal{Y}_b}$
(Lemma 2.4).
Consider the Hodge bundles (with respect to the Zariski topology)
where
![]() $\Omega _{\mathcal{X} / B}^{\bullet }$
is the algebraic de Rham complex. Since the family
$\Omega _{\mathcal{X} / B}^{\bullet }$
is the algebraic de Rham complex. Since the family
![]() $\mathcal{X} \to B$
is fixed, we suppress it from the notation. Recall that Hodge bundles behave well with respect to base change and the fibre of
$\mathcal{X} \to B$
is fixed, we suppress it from the notation. Recall that Hodge bundles behave well with respect to base change and the fibre of
![]() $\mathcal{H}^{2p}_{{\rm dR}}$
over a closed point
$\mathcal{H}^{2p}_{{\rm dR}}$
over a closed point
![]() $b \in B$
is
$b \in B$
is
where on the right-hand side, we consider
![]() $\mathcal{X}_b$
with the complex analytic topology. We fix a flat section with respect to the Gauß–Manin connection
$\mathcal{X}_b$
with the complex analytic topology. We fix a flat section with respect to the Gauß–Manin connection
 \begin{align*} \widetilde {v} = (\widetilde {v}_0, \widetilde {v}_1, \widetilde {v}_2) \in \bigoplus _{p=0}^{2} \Gamma (B, \mathcal {H}^{2p}_{\mathrm {dR}}). \end{align*}
\begin{align*} \widetilde {v} = (\widetilde {v}_0, \widetilde {v}_1, \widetilde {v}_2) \in \bigoplus _{p=0}^{2} \Gamma (B, \mathcal {H}^{2p}_{\mathrm {dR}}). \end{align*}
Fix a family of polarizations
![]() $\mathcal{H}$
on
$\mathcal{H}$
on
![]() $\mathcal{X}$
. Denote by
$\mathcal{X}$
. Denote by
the moduli space parametrizing
![]() $\mathcal{H}_b$
-stable
$\mathcal{H}_b$
-stable
![]() $\mathcal{Y}_b$
-sheaves
$\mathcal{Y}_b$
-sheaves
![]() $F$
with Chern character
$F$
with Chern character
![]() ${{\rm ch}}_{G_b}(F) = \widetilde{v}_b$
, for some closed point
${{\rm ch}}_{G_b}(F) = \widetilde{v}_b$
, for some closed point
![]() $b \in B$
. This is the relative version over
$b \in B$
. This is the relative version over
![]() $B$
of the moduli spaces constructed by Yoshioka [Reference YoshiokaYos06]. Note that for any closed point
$B$
of the moduli spaces constructed by Yoshioka [Reference YoshiokaYos06]. Note that for any closed point
![]() $b \in B$
, we have a Cartesian diagram
$b \in B$
, we have a Cartesian diagram
![]()
where
![]() $M_b := M_{\mathcal{Y}_b}^{\mathcal{H}_b} (\widetilde{v}_b)$
.
$M_b := M_{\mathcal{Y}_b}^{\mathcal{H}_b} (\widetilde{v}_b)$
.
Remark 4.3. In order for these moduli spaces to be non-empty, we must have
 \begin{align} \widetilde{v}_b \in \bigoplus _{p=0}^{2} H^{p,p}(\mathcal{X}_b), \end{align}
\begin{align} \widetilde{v}_b \in \bigoplus _{p=0}^{2} H^{p,p}(\mathcal{X}_b), \end{align}
for some closed point
![]() $b \in B$
. Suppose
$b \in B$
. Suppose
![]() $B$
is quasi-projective. Then Deligne’s invariant cycle theorem implies that (11) holds for all closed points
$B$
is quasi-projective. Then Deligne’s invariant cycle theorem implies that (11) holds for all closed points
![]() $b \in B$
[Reference EduardoCat14, Proposition 11.3.5].
$b \in B$
[Reference EduardoCat14, Proposition 11.3.5].
Remark 4.4. Note that we do not fix a family of
![]() $B$
-fields. Such a family would be a flat section
$B$
-fields. Such a family would be a flat section
![]() $\widetilde{\xi } \in \Gamma (B, \mathcal{H}^{2}_{{\rm dR}})$
such that
$\widetilde{\xi } \in \Gamma (B, \mathcal{H}^{2}_{{\rm dR}})$
such that
![]() $\widetilde{\xi }_b$
is integral for all
$\widetilde{\xi }_b$
is integral for all
![]() $b \in B$
. We are typically interested in families where the class
$b \in B$
. We are typically interested in families where the class
![]() $[\widetilde{\xi }_b] \in H^2(\mathcal{X}_b,\mu _r)$
has non-trivial Brauer class for some
$[\widetilde{\xi }_b] \in H^2(\mathcal{X}_b,\mu _r)$
has non-trivial Brauer class for some
![]() $b \in B$
and trivial Brauer class for another
$b \in B$
and trivial Brauer class for another
![]() $b \in B$
. Recall that
$b \in B$
. Recall that
![]() $[\widetilde{\xi }_b] \in H^2(\mathcal{X}_b,\mu _r)$
has trivial Brauer class if and only if
$[\widetilde{\xi }_b] \in H^2(\mathcal{X}_b,\mu _r)$
has trivial Brauer class if and only if
![]() $\widetilde{\xi }_b$
has Hodge type
$\widetilde{\xi }_b$
has Hodge type
![]() $(1,1)$
modulo
$(1,1)$
modulo
![]() $r H^2(\mathcal{X}_b,\mathbb{Z})$
(§2.1). If in fact
$r H^2(\mathcal{X}_b,\mathbb{Z})$
(§2.1). If in fact
![]() $\widetilde{\xi }_b$
itself has type
$\widetilde{\xi }_b$
itself has type
![]() $(1,1)$
for some
$(1,1)$
for some
![]() $b \in B$
(and
$b \in B$
(and
![]() $B$
is quasi-projective), then it has type
$B$
is quasi-projective), then it has type
![]() $(1,1)$
for all
$(1,1)$
for all
![]() $b \in B$
by Deligne’s invariant cycle theorem, which is too restrictive for our purposes.
$b \in B$
by Deligne’s invariant cycle theorem, which is too restrictive for our purposes.
By [Reference Huybrechts and ThomasHT09, Theorem 4.1], we have a relative obstruction theory
For each closed point
![]() $b \in B$
, consider the inclusion
$b \in B$
, consider the inclusion
![]() $j_b : \mathcal{X}_b \hookrightarrow \mathcal{X}$
, then we obtain an induced map
$j_b : \mathcal{X}_b \hookrightarrow \mathcal{X}$
, then we obtain an induced map
which is the perfect obstruction theory of Proposition 4.1. Since the base
![]() $B$
is connected, the topological number
$B$
is connected, the topological number
does not depend on the closed point
![]() $b \in B$
. We obtain a cycle class [Reference Huybrechts and ThomasHT09, Corollary 4.3]
$b \in B$
. We obtain a cycle class [Reference Huybrechts and ThomasHT09, Corollary 4.3]
such that for all closed points
![]() $b \in B$
we have
$b \in B$
we have
where
![]() $i_b^! : A_*(M_{\mathcal{Y}/B}) \to A_*(M_{b})$
is the refined Gysin pull-back [Reference FultonFul98] for the Cartesian diagram (4.1).
$i_b^! : A_*(M_{\mathcal{Y}/B}) \to A_*(M_{b})$
is the refined Gysin pull-back [Reference FultonFul98] for the Cartesian diagram (4.1).
4.2 The
 ${\rm SL}_r$
and
${\rm SL}_r$
and
 ${\rm PGL}_r$
generating function
${\rm PGL}_r$
generating function
Let
![]() $R$
be a commutative
$R$
be a commutative
![]() $\mathbb{Q}$
-algebra e.g.
$\mathbb{Q}$
-algebra e.g.
![]() $\mathbb{Q}$
or a polynomial algebra over
$\mathbb{Q}$
or a polynomial algebra over
![]() $\mathbb{Q}$
. Fix
$\mathbb{Q}$
. Fix
![]() $v \in \mathbb{Z}_{\geq 0}$
, and
$v \in \mathbb{Z}_{\geq 0}$
, and
![]() $\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
for some
$\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
for some
![]() $N \in \mathbb{Z}_{\geq 0}$
. Let
$N \in \mathbb{Z}_{\geq 0}$
. Let
![]() $(\underline{\alpha _0},\underline{\alpha _1},\ldots, \underline{\alpha _N})$
be a list of variables and let
$(\underline{\alpha _0},\underline{\alpha _1},\ldots, \underline{\alpha _N})$
be a list of variables and let
![]() $\underline{r}$
be a further variable. Let
$\underline{r}$
be a further variable. Let
![]() $\mathsf{P}_{v,\boldsymbol{a}}$
be a formal power series, with coefficients in
$\mathsf{P}_{v,\boldsymbol{a}}$
be a formal power series, with coefficients in
![]() $R(\underline{r})$
, in the following formal symbols:
$R(\underline{r})$
, in the following formal symbols:
 \begin{align*} & \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \quad \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \\ & \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_2(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ), \quad \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)^2} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \\ & c_j(R\mathcal{H}{\textit{om}}_{\pi _M}(\underline{\mathcal{E}}, \underline{\mathcal{E}})[1]), \end{align*}
\begin{align*} & \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \quad \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \\ & \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_2(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ), \quad \pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)^2} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ), \\ & c_j(R\mathcal{H}{\textit{om}}_{\pi _M}(\underline{\mathcal{E}}, \underline{\mathcal{E}})[1]), \end{align*}
where
![]() $i=0,\ldots, N$
and
$i=0,\ldots, N$
and
![]() $k,j \in \mathbb{Z}_{\geq 0}$
, and
$k,j \in \mathbb{Z}_{\geq 0}$
, and
![]() $\underline{\alpha _i}, \underline{\alpha _i c_1(X)}, \ldots, \underline{\mathcal{E}}$
are viewed as formal variables. Define degrees
$\underline{\alpha _i}, \underline{\alpha _i c_1(X)}, \ldots, \underline{\mathcal{E}}$
are viewed as formal variables. Define degrees
![]() $\deg \, c_j(\cdot ) = j$
and
$\deg \, c_j(\cdot ) = j$
and
 \begin{align*} \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k-2, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k - 1, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_2(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)^2} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ) & = a_i + k, \end{align*}
\begin{align*} \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k-2, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k - 1, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_2(X)} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{- {1 \over \underline{r}}})\Big ) & = a_i + k, \\ \deg \,\pi _{M*}\Big ( \pi _X^* \underline{\alpha _i c_1(X)^2} \cap{{\rm ch}}_{k}( \underline{\mathcal{E}} \otimes \det (\underline{\mathcal{E}})^{-{1 \over \underline{r}}})\Big ) & = a_i + k, \end{align*}
where
![]() $i=0,\ldots, N$
and we take
$i=0,\ldots, N$
and we take
![]() $a_0:=0$
. We assume that the formal power series
$a_0:=0$
. We assume that the formal power series
![]() $\mathsf{P}_{v,\boldsymbol{a}}$
has only finitely many terms in each degree. We refer to
$\mathsf{P}_{v,\boldsymbol{a}}$
has only finitely many terms in each degree. We refer to
![]() $\mathsf{P}_{v,\boldsymbol{a}}$
as a formal insertion. The reader who is only interested in virtual Euler characteristics can take
$\mathsf{P}_{v,\boldsymbol{a}}$
as a formal insertion. The reader who is only interested in virtual Euler characteristics can take
![]() $\mathsf{P}_v = c_v(R\mathcal{H}{\textit{om}}_{\pi _M}(\underline{\mathcal{E}}, \underline{\mathcal{E}})[1])$
.
$\mathsf{P}_v = c_v(R\mathcal{H}{\textit{om}}_{\pi _M}(\underline{\mathcal{E}}, \underline{\mathcal{E}})[1])$
.
Keeping
![]() $\boldsymbol{a}$
,
$\boldsymbol{a}$
,
![]() $\underline{r}$
fixed as above, we now consider a sequence of formal insertions
$\underline{r}$
fixed as above, we now consider a sequence of formal insertions
![]() $\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
.Footnote
15
Let
$\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
.Footnote
15
Let
![]() $r \gt 1$
, let
$r \gt 1$
, let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
, and
$H_1(X,\mathbb{Z}) = 0$
, and
![]() $\boldsymbol{\alpha } = (\alpha _1, \ldots, \alpha _N) \in H^{*}(X,\mathbb{Q})^N$
algebraic classes with
$\boldsymbol{\alpha } = (\alpha _1, \ldots, \alpha _N) \in H^{*}(X,\mathbb{Q})^N$
algebraic classes with
![]() $\deg (\alpha _i) = a_i$
for all
$\deg (\alpha _i) = a_i$
for all
![]() $i=1, \ldots, N$
.
$i=1, \ldots, N$
.
 ${\rm SL}_r$
-invariants.
${\rm SL}_r$
-invariants.
As in the introduction, denote by
![]() $M:=M_X^H(r,c_1,c_2)$
the Gieseker–Maruyama–Simpson moduli space of rank
$M:=M_X^H(r,c_1,c_2)$
the Gieseker–Maruyama–Simpson moduli space of rank
![]() $r$
Gieseker
$r$
Gieseker
![]() $H$
-stable sheaves on
$H$
-stable sheaves on
![]() $X$
with Chern classes
$X$
with Chern classes
![]() $c_1,c_2$
[Reference Huybrechts and LehnHL10]. Suppose, for the moment, that there exists a universal sheaf
$c_1,c_2$
[Reference Huybrechts and LehnHL10]. Suppose, for the moment, that there exists a universal sheaf
![]() $\mathcal{E}$
on
$\mathcal{E}$
on
![]() $X \times M$
such that the line bundle
$X \times M$
such that the line bundle
![]() $\det (\mathcal{E})$
has an
$\det (\mathcal{E})$
has an
![]() $r$
th root. We drop these two assumptions in Remark 4.7. Take
$r$
th root. We drop these two assumptions in Remark 4.7. Take
Then the evaluation
![]() $\mathsf{P}_{v,\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M,\mathcal{E})$
is defined as the cohomology class on
$\mathsf{P}_{v,\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M,\mathcal{E})$
is defined as the cohomology class on
![]() $M$
obtained from
$M$
obtained from
![]() $\mathsf{P}_{v,\boldsymbol{a}}$
by substitutingFootnote
16
$\mathsf{P}_{v,\boldsymbol{a}}$
by substitutingFootnote
16
 \begin{align*} & \underline{\alpha _0} = 1, \quad \underline{\alpha _0 c_1(X)} = c_1(X), \quad \underline{\alpha _0 c_2(X)} = c_2(X), \quad \underline{\alpha _0 c_1(X)^2} = c_1(X)^2, \quad \underline{\mathcal{E}} = \mathcal{E}, \\ & \underline{r} = r, \quad \underline{\alpha _i} = \alpha _i, \quad \underline{\alpha _i c_1(X)} = \alpha _i c_1(X), \quad \underline{\alpha _i c_2(X)} = \alpha _i c_2(X), \quad \underline{\alpha _i c_1(X)^2} = \alpha _i c_1(X)^2 \end{align*}
\begin{align*} & \underline{\alpha _0} = 1, \quad \underline{\alpha _0 c_1(X)} = c_1(X), \quad \underline{\alpha _0 c_2(X)} = c_2(X), \quad \underline{\alpha _0 c_1(X)^2} = c_1(X)^2, \quad \underline{\mathcal{E}} = \mathcal{E}, \\ & \underline{r} = r, \quad \underline{\alpha _i} = \alpha _i, \quad \underline{\alpha _i c_1(X)} = \alpha _i c_1(X), \quad \underline{\alpha _i c_2(X)} = \alpha _i c_2(X), \quad \underline{\alpha _i c_1(X)^2} = \alpha _i c_1(X)^2 \end{align*}
for all
![]() $i=1, \ldots, N$
, where
$i=1, \ldots, N$
, where
![]() $\pi _X : X \times M \to M$
,
$\pi _X : X \times M \to M$
,
![]() $\pi _M : X \times M \to M$
denote the projections.
$\pi _M : X \times M \to M$
denote the projections.
Definition 4.5. Fix a first Chern class
![]() $c_1 \in H^2(X,\mathbb{Z})$
. Suppose there are no rank
$c_1 \in H^2(X,\mathbb{Z})$
. Suppose there are no rank
![]() $r$
strictly Gieseker
$r$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with first Chern class
$X$
with first Chern class
![]() $c_1$
(this is the case, for example, when
$c_1$
(this is the case, for example, when
![]() $\gcd (r,c_1H)=1$
). We define the
$\gcd (r,c_1H)=1$
). We define the
![]() ${\rm SL}_r$
generating function of
${\rm SL}_r$
generating function of
![]() $(X,H), c_1$
associated with formal insertions
$(X,H), c_1$
associated with formal insertions
![]() $\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
by
$\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
by
where
![]() ${\rm vd}(r,c_1,c_2)$
was defined in (10).
${\rm vd}(r,c_1,c_2)$
was defined in (10).
 ${\rm PGL}_r$
-invariants.
${\rm PGL}_r$
-invariants.
Fix a class
![]() $w \in H^2(X,\mu _r)$
. By Theorem 2.16, there exists a degree
$w \in H^2(X,\mu _r)$
. By Theorem 2.16, there exists a degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
such that
$Y \to X$
such that
![]() $w(Y) = w$
. Choose a representative
$w(Y) = w$
. Choose a representative
![]() $\xi \in H^2(X,\mathbb{Z})$
of
$\xi \in H^2(X,\mathbb{Z})$
of
![]() $w$
, i.e.
$w$
, i.e.
![]() $w = [\xi ]$
(Lemma 3.1). As in § 3.2, denote by
$w = [\xi ]$
(Lemma 3.1). As in § 3.2, denote by
![]() $M:=M_{Y,\xi /r}^H(r,\xi, c_2)$
Yoshioka’s moduli space of
$M:=M_{Y,\xi /r}^H(r,\xi, c_2)$
Yoshioka’s moduli space of
![]() $H$
-stable
$H$
-stable
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $F$
satisfying
$F$
satisfying
Note that we have ‘switched on’ the
![]() $B$
-field so that
$B$
-field so that
![]() $c_2 \in \mathbb{Z}$
(Proposition 3.3). Also note that we choose the rank of
$c_2 \in \mathbb{Z}$
(Proposition 3.3). Also note that we choose the rank of
![]() $F$
equal to the degree of
$F$
equal to the degree of
![]() $Y$
and ‘twisted’ first Chern class equal to
$Y$
and ‘twisted’ first Chern class equal to
![]() $\xi$
.Footnote
17
Suppose, for the moment, that there exists a universal sheaf
$\xi$
.Footnote
17
Suppose, for the moment, that there exists a universal sheaf
![]() $\mathcal{E}$
on
$\mathcal{E}$
on
![]() $Y \times M$
such that the line bundle
$Y \times M$
such that the line bundle
![]() $\det (\mathcal{E})$
has an
$\det (\mathcal{E})$
has an
![]() $r$
th root. We drop these two assumptions in Remark 4.7. Take
$r$
th root. We drop these two assumptions in Remark 4.7. Take
The evaluation
![]() $\mathsf{P}_{v,\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M,\mathcal{E})$
is defined as the cohomology class on
$\mathsf{P}_{v,\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M,\mathcal{E})$
is defined as the cohomology class on
![]() $M$
obtained from
$M$
obtained from
![]() $\mathsf{P}_{v,\boldsymbol{a}}$
by substituting
$\mathsf{P}_{v,\boldsymbol{a}}$
by substituting
where
![]() $\pi$
is the base change of
$\pi$
is the base change of
![]() $\pi : Y \to X$
to
$\pi : Y \to X$
to
![]() $Y \times M$
, and furthermore by substituting
$Y \times M$
, and furthermore by substituting
 \begin{align*} & \underline{\alpha _0} = 1, \quad \underline{\alpha _0 c_1(X)} = c_1(X), \quad \underline{\alpha _0 c_2(X)} = c_2(X), \quad \underline{\alpha _0 c_1(X)^2} = c_1(X)^2, \\ & \underline{r} = r, \quad \underline{\alpha _i} = \alpha _i, \quad \underline{\alpha _i c_1(X)} = \alpha _i c_1(X), \quad \underline{\alpha _i c_2(X)} = \alpha _i c_2(X), \quad \underline{\alpha _i c_1(X)^2} = \alpha _i c_1(X)^2, \end{align*}
\begin{align*} & \underline{\alpha _0} = 1, \quad \underline{\alpha _0 c_1(X)} = c_1(X), \quad \underline{\alpha _0 c_2(X)} = c_2(X), \quad \underline{\alpha _0 c_1(X)^2} = c_1(X)^2, \\ & \underline{r} = r, \quad \underline{\alpha _i} = \alpha _i, \quad \underline{\alpha _i c_1(X)} = \alpha _i c_1(X), \quad \underline{\alpha _i c_2(X)} = \alpha _i c_2(X), \quad \underline{\alpha _i c_1(X)^2} = \alpha _i c_1(X)^2, \end{align*}
for all
![]() $i=1, \ldots, N$
, where
$i=1, \ldots, N$
, where
![]() $\pi _X : X \times M \to M$
,
$\pi _X : X \times M \to M$
,
![]() $\pi _M : X \times M \to M$
denote the projections.
$\pi _M : X \times M \to M$
denote the projections.
Definition 4.6. Fix
![]() $w \in H^2(X,\mu _r)$
. Choose a degree
$w \in H^2(X,\mu _r)$
. Choose a degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
with
$Y \to X$
with
![]() $w(Y) = w$
and choose a representative
$w(Y) = w$
and choose a representative
![]() $\xi \in H^2(X,\mathbb{Z})$
of
$\xi \in H^2(X,\mathbb{Z})$
of
![]() $w$
. Suppose there are no rank
$w$
. Suppose there are no rank
![]() $r$
strictly
$r$
strictly
![]() $H$
-semistable
$H$
-semistable
![]() $Y$
-sheaves
$Y$
-sheaves
![]() $F$
with
$F$
with
![]() ${\rm ch}_{G}^{\xi }(F) = (r,\xi, {1 \over 2} \xi^2 - c_2)$
for any
${\rm ch}_{G}^{\xi }(F) = (r,\xi, {1 \over 2} \xi^2 - c_2)$
for any
![]() $c_2$
(this is the case, for example, when the Brauer class
$c_2$
(this is the case, for example, when the Brauer class
![]() $o(w) \in H^2(X,\mathbb{G}_m)$
has order
$o(w) \in H^2(X,\mathbb{G}_m)$
has order
![]() $r$
by Remark 3.5). We define the
$r$
by Remark 3.5). We define the
![]() ${\rm PGL}_r$
generating function of
${\rm PGL}_r$
generating function of
![]() $(X,H), w$
associated with formal insertions
$(X,H), w$
associated with formal insertions
![]() $\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
by
$\mathsf{P} := \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
by
where
![]() ${\rm vd}(r,\xi, c_2)$
was defined in (10). As we will see below (Proposition 4.9), this generating function does not depend on the choice of
${\rm vd}(r,\xi, c_2)$
was defined in (10). As we will see below (Proposition 4.9), this generating function does not depend on the choice of
![]() $Y, \xi$
on the right-hand side, justifying the notation.
$Y, \xi$
on the right-hand side, justifying the notation.
Remark 4.7. In each of the above two settings, in general a universal sheaf
![]() $\mathcal{E}$
on
$\mathcal{E}$
on
![]() $X \times M$
(respectively
$X \times M$
(respectively
![]() $Y \times M$
) may only exist étale locally. However, note that the following complex and sheaf always exist globally by [Reference CăldăraruCal00, Theorem 2.2.4] (see also [Reference Huybrechts and LehnHL10, §10.2]):
$Y \times M$
) may only exist étale locally. However, note that the following complex and sheaf always exist globally by [Reference CăldăraruCal00, Theorem 2.2.4] (see also [Reference Huybrechts and LehnHL10, §10.2]):
Note furthermore that for any class
![]() $V \in 1+K^0(X \times M)$
, we can define an
$V \in 1+K^0(X \times M)$
, we can define an
![]() $r$
th root operation
$r$
th root operation
precisely as in [Reference Oh and ThomasOT23, Lemma 5.1] (which handles the
![]() $r=2$
case, but the arguments generalize). Then we set
$r=2$
case, but the arguments generalize). Then we set
and similarly for
![]() ${{\rm ch}}(\pi _*(\mathcal{E} \otimes (\det (\mathcal{E}))^{-{1 \over r}}))$
for a degree
${{\rm ch}}(\pi _*(\mathcal{E} \otimes (\det (\mathcal{E}))^{-{1 \over r}}))$
for a degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $\pi : Y \to X$
.
$\pi : Y \to X$
.
We will now prove that the generating function
![]() $\mathsf{Z}^{{\rm PGL}_r, \mathsf{P}}_{(X,H), w}(q)$
does not depend on the choice of Brauer–Severi variety
$\mathsf{Z}^{{\rm PGL}_r, \mathsf{P}}_{(X,H), w}(q)$
does not depend on the choice of Brauer–Severi variety
![]() $Y$
with Stiefel–Whitney class
$Y$
with Stiefel–Whitney class
![]() $w$
, or representative
$w$
, or representative
![]() $\xi$
of
$\xi$
of
![]() $w$
. Here we will make crucial use of [Reference YoshiokaYos06, Lemma 3.5], which establishes the relevant isomorphism of moduli spaces. We extend this result to also include an isomorphism of virtual tangent bundles. Furthermore, we prove [Reference YoshiokaYos06, Lemma 3.5] in a slightly different way, and we will provide more details and include some intermediate steps that are useful on their own. We first recall Yoshioka’s set-up.
$w$
. Here we will make crucial use of [Reference YoshiokaYos06, Lemma 3.5], which establishes the relevant isomorphism of moduli spaces. We extend this result to also include an isomorphism of virtual tangent bundles. Furthermore, we prove [Reference YoshiokaYos06, Lemma 3.5] in a slightly different way, and we will provide more details and include some intermediate steps that are useful on their own. We first recall Yoshioka’s set-up.
Suppose
![]() $p_1 : Y_1 \to X$
and
$p_1 : Y_1 \to X$
and
![]() $p_2 : Y_2 \to X$
are two Brauer–Severi varieties with the same Brauer class
$p_2 : Y_2 \to X$
are two Brauer–Severi varieties with the same Brauer class
![]() $o(w(Y_1)) = o(w(Y_2))$
(we will later assume
$o(w(Y_1)) = o(w(Y_2))$
(we will later assume
![]() $Y_1$
,
$Y_1$
,
![]() $Y_2$
have the same degree and
$Y_2$
have the same degree and
![]() $w(Y_1) = w(Y_2)$
). Denote the projections
$w(Y_1) = w(Y_2)$
). Denote the projections
![]() $Y_1 \times _X Y_2 \to Y_1$
and
$Y_1 \times _X Y_2 \to Y_1$
and
![]() $Y_1 \times _X Y_2 \to Y_2$
by
$Y_1 \times _X Y_2 \to Y_2$
by
![]() $\pi _1$
and
$\pi _1$
and
![]() $\pi _2$
, respectively. Yoshioka shows that there exists a line bundle
$\pi _2$
, respectively. Yoshioka shows that there exists a line bundle
![]() $L$
on
$L$
on
![]() $Y_1 \times _X Y_2$
such that the Fourier–Mukai transform
$Y_1 \times _X Y_2$
such that the Fourier–Mukai transform
defines an equivalence of categories [Reference YoshiokaYos06, Lemma 1.7]. Note that we can always replace
![]() $L$
by
$L$
by
![]() $L \otimes \pi _2^*p_2^*P$
with
$L \otimes \pi _2^*p_2^*P$
with
![]() $P$
a line bundle on
$P$
a line bundle on
![]() $X$
, something we will do later. We first record the following identities.
$X$
, something we will do later. We first record the following identities.
Lemma 4.8.
Let
![]() $F$
be an
$F$
be an
![]() $Y_1$
-sheaf. The canonical map
$Y_1$
-sheaf. The canonical map
is an isomorphism, i.e.
![]() $\pi _1^*F \otimes L$
is globally generated relative to
$\pi _1^*F \otimes L$
is globally generated relative to
![]() $\pi _2$
. If
$\pi _2$
. If
![]() $F^{\prime}$
is another
$F^{\prime}$
is another
![]() $Y_1$
-sheaf that is locally free, we have that
$Y_1$
-sheaf that is locally free, we have that
Proof.
We can check the first statement étale locally, where the Brauer–Severi varieties are trivial. Then, the sheaves
![]() $\mathcal{O}_{Y_1}(1)$
and
$\mathcal{O}_{Y_1}(1)$
and
![]() $\mathcal{O}_{Y_2}(1)$
exist. Yoshioka has already shown that
$\mathcal{O}_{Y_2}(1)$
exist. Yoshioka has already shown that
![]() $F(-1)$
is globally generated relative to
$F(-1)$
is globally generated relative to
![]() $p_1$
. Then, by base change,
$p_1$
. Then, by base change,
![]() $\pi _1^*(F(-1))$
is globally generated relative to
$\pi _1^*(F(-1))$
is globally generated relative to
![]() $\pi _2$
, and also,
$\pi _2$
, and also,
![]() $\pi _1^*(F(-1)) \otimes \pi _2^*Q$
is globally generated relative to
$\pi _1^*(F(-1)) \otimes \pi _2^*Q$
is globally generated relative to
![]() $\pi _2$
for any line bundle
$\pi _2$
for any line bundle
![]() $Q$
. The claim now follows from the construction of
$Q$
. The claim now follows from the construction of
![]() $L$
by Yoshioka: on this étale cover it is given by
$L$
by Yoshioka: on this étale cover it is given by
![]() $\mathcal{O}_{Y_1}(-1) \boxtimes (\mathcal{O}_{Y_2}(1) \otimes p_2^*P)$
for
$\mathcal{O}_{Y_1}(-1) \boxtimes (\mathcal{O}_{Y_2}(1) \otimes p_2^*P)$
for
![]() $P$
any line bundle on
$P$
any line bundle on
![]() $X$
.
$X$
.
The second statement directly follows from the first.
Proposition 4.9.
The generating function
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{P}}(q)$
does not depend on the choice of degree
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{P}}(q)$
does not depend on the choice of degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to X$
with
$Y \to X$
with
![]() $w(Y) = w$
or representative
$w(Y) = w$
or representative
![]() $\xi \in H^2(X,\mathbb{Z})$
of
$\xi \in H^2(X,\mathbb{Z})$
of
![]() $w$
.
$w$
.
Proof.
We start with the independence of
![]() $Y$
. Using the above notation, let
$Y$
. Using the above notation, let
![]() $Y_1, Y_2$
be degree
$Y_1, Y_2$
be degree
![]() $r$
Brauer–Severi varieties on
$r$
Brauer–Severi varieties on
![]() $X$
with
$X$
with
![]() $w(Y_1) = w(Y_2) = w$
. We will first show that
$w(Y_1) = w(Y_2) = w$
. We will first show that
![]() $\Xi$
induces an isomorphism between moduli spaces, and then that it preserves the obstruction theory and the generating function.
$\Xi$
induces an isomorphism between moduli spaces, and then that it preserves the obstruction theory and the generating function.
We first want to prove that
![]() $\Xi$
preserves the Chern character, in order to have a chance at showing it preserves the moduli spaces. Denote by
$\Xi$
preserves the Chern character, in order to have a chance at showing it preserves the moduli spaces. Denote by
![]() $G_i$
the unique (up to scaling) non-trivial extension of
$G_i$
the unique (up to scaling) non-trivial extension of
![]() $T_{Y_i/X}$
by
$T_{Y_i/X}$
by
![]() $\mathcal{O}_{Y_i}$
(Lemma 2.4). We consider the equality
$\mathcal{O}_{Y_i}$
(Lemma 2.4). We consider the equality
![]() ${{\rm ch}}_{G_1}(F) ={{\rm ch}}_{G_2}(\Xi (F))$
for any
${{\rm ch}}_{G_1}(F) ={{\rm ch}}_{G_2}(\Xi (F))$
for any
![]() $Y_1$
-sheaf
$Y_1$
-sheaf
![]() $F$
of positive rank. It suffices to show this equality on
$F$
of positive rank. It suffices to show this equality on
![]() $Y_1 \times _X Y_2$
modulo
$Y_1 \times _X Y_2$
modulo
![]() $H^{\geq 6}$
, since
$H^{\geq 6}$
, since
![]() $Y_1 \times _X Y_2 \to X$
induces an injective map on cohomology. Using the fact that
$Y_1 \times _X Y_2 \to X$
induces an injective map on cohomology. Using the fact that
![]() $F, G_1$
are
$F, G_1$
are
![]() $Y_1$
-sheaves and
$Y_1$
-sheaves and
![]() $\Xi (F), G_2$
are
$\Xi (F), G_2$
are
![]() $Y_2$
-sheaves (Definition 2.17), it suffices to prove the following equality modulo
$Y_2$
-sheaves (Definition 2.17), it suffices to prove the following equality modulo
![]() $H^{\geq 6}$
:
$H^{\geq 6}$
:
By Lemma 4.8, this is equivalent to the following equation modulo
![]() $H^{\geq 6}$
:
$H^{\geq 6}$
:
 \begin{align*}{{\rm ch}} & \left ( (\pi _1^* F)^{\otimes 2} \otimes \pi _1^*G_1^\vee \otimes \pi _2^*(\Xi G_1)^\vee \otimes \pi _2^*G_2 \otimes \pi _2^*G_2^\vee \right )\\ & ={{\rm ch}} \left ( (\pi _1^* F)^{\otimes 2} \otimes (\pi _2^*G_2^\vee )^{\otimes 2} \otimes \pi _2^*(\Xi G_1) \otimes \pi _1^*G_1^\vee \right ), \end{align*}
\begin{align*}{{\rm ch}} & \left ( (\pi _1^* F)^{\otimes 2} \otimes \pi _1^*G_1^\vee \otimes \pi _2^*(\Xi G_1)^\vee \otimes \pi _2^*G_2 \otimes \pi _2^*G_2^\vee \right )\\ & ={{\rm ch}} \left ( (\pi _1^* F)^{\otimes 2} \otimes (\pi _2^*G_2^\vee )^{\otimes 2} \otimes \pi _2^*(\Xi G_1) \otimes \pi _1^*G_1^\vee \right ), \end{align*}
which can then be rearranged to give
Thus, to obtain the Chern character equality, it suffices to show that
![]() ${{\rm ch}}(\Xi (G_1)^\vee \otimes G_2) ={{\rm ch}}(G_2^\vee \otimes \Xi (G_1))$
modulo
${{\rm ch}}(\Xi (G_1)^\vee \otimes G_2) ={{\rm ch}}(G_2^\vee \otimes \Xi (G_1))$
modulo
![]() $H^{\geq 6}(Y_2,\mathbb{Q})$
. Since,
$H^{\geq 6}(Y_2,\mathbb{Q})$
. Since,
![]() ${\rm ch}_0$
and
${\rm ch}_0$
and
![]() ${\rm ch}_2$
already agree, we only have to worry about the
${\rm ch}_2$
already agree, we only have to worry about the
![]() $c_1$
. We show that we can replace
$c_1$
. We show that we can replace
![]() $L$
by
$L$
by
![]() $L \otimes \pi _2^*p_2^*P$
for some
$L \otimes \pi _2^*p_2^*P$
for some
![]() $P \in {\rm Pic}(X)$
such that
$P \in {\rm Pic}(X)$
such that
![]() $c_1(G_2) = c_1(\Xi (G_1))$
, which proves what we want. Changing
$c_1(G_2) = c_1(\Xi (G_1))$
, which proves what we want. Changing
![]() $L$
by
$L$
by
![]() $L \otimes \pi _2^* p_2^* P$
replaces
$L \otimes \pi _2^* p_2^* P$
replaces
![]() $\Xi$
by
$\Xi$
by
![]() $F \mapsto p_2^*P \otimes \Xi (F)$
, so, in particular, it replaces
$F \mapsto p_2^*P \otimes \Xi (F)$
, so, in particular, it replaces
![]() $c_1(\Xi (G_1))$
by
$c_1(\Xi (G_1))$
by
![]() $c_1(\Xi (G_1)) + rp_2^*c_1(P)$
. Thus, in order to find the desired
$c_1(\Xi (G_1)) + rp_2^*c_1(P)$
. Thus, in order to find the desired
![]() $P$
, we have to show that
$P$
, we have to show that
The equality
![]() $p_2^*p_{2*}(\Xi (G_1) \otimes G_2^\vee ) \cong \Xi (G_1) \otimes G_2^\vee$
, which holds since
$p_2^*p_{2*}(\Xi (G_1) \otimes G_2^\vee ) \cong \Xi (G_1) \otimes G_2^\vee$
, which holds since
![]() $\Xi (G_1)$
is a
$\Xi (G_1)$
is a
![]() $Y_2$
-sheaf, already implies that
$Y_2$
-sheaf, already implies that
![]() $r(c_1(G_2)-c_1(\Xi (G_1)))$
lies in
$r(c_1(G_2)-c_1(\Xi (G_1)))$
lies in
![]() $r \cdot p_2^*(H^2(X, \mathbb{Z}) \cap H^{1,1}(X))$
, which implies that
$r \cdot p_2^*(H^2(X, \mathbb{Z}) \cap H^{1,1}(X))$
, which implies that
To get the factor
![]() $r$
, we see that the image of
$r$
, we see that the image of
![]() $c_1(G_2) - c_1(\Xi (G_1))$
in
$c_1(G_2) - c_1(\Xi (G_1))$
in
![]() $H^2(Y_2, \mu _r)$
is
$H^2(Y_2, \mu _r)$
is
![]() $p_2^*w - p_2^*w=0$
, by the assumption
$p_2^*w - p_2^*w=0$
, by the assumption
![]() $w(Y_1) = w(Y_2) = w$
and [Reference YoshiokaYos06, Lemma 1.3, 1.8]. Using the explicit form of
$w(Y_1) = w(Y_2) = w$
and [Reference YoshiokaYos06, Lemma 1.3, 1.8]. Using the explicit form of
![]() $H^2(Y_2, \mathbb{Z}) = p_2^*H^0(X,\mathbb{Z}) \oplus p_2^*H^2(X, \mathbb{Z})$
, we see that (13) is satisfied. This shows that we can pick
$H^2(Y_2, \mathbb{Z}) = p_2^*H^0(X,\mathbb{Z}) \oplus p_2^*H^2(X, \mathbb{Z})$
, we see that (13) is satisfied. This shows that we can pick
![]() $\Xi$
such that it preserves the Chern character. For the rest of the proof, we will use this
$\Xi$
such that it preserves the Chern character. For the rest of the proof, we will use this
![]() $\Xi$
.
$\Xi$
.
It is now not hard to show that
where
![]() $c$
is a constant that does not depend on
$c$
is a constant that does not depend on
![]() $F$
. Therefore
$F$
. Therefore
![]() $\Xi$
preserves stability. Since
$\Xi$
preserves stability. Since
![]() $\Xi$
preserves the Chern character and the stability condition, we obtain an isomorphism
$\Xi$
preserves the Chern character and the stability condition, we obtain an isomorphism
for any lift
![]() $\xi$
of
$\xi$
of
![]() $w$
and any
$w$
and any
![]() $c_2 \in \mathbb{Z}$
.
$c_2 \in \mathbb{Z}$
.
Suppose there exists a universal sheaf
![]() $\mathcal{E}_1$
on
$\mathcal{E}_1$
on
![]() $Y_1 \times M_1$
, where
$Y_1 \times M_1$
, where
![]() $M_i:=M_{Y_i,\xi /r}^H(r,\xi, c_2)$
. Then
$M_i:=M_{Y_i,\xi /r}^H(r,\xi, c_2)$
. Then
is a universal sheaf on
![]() $Y_2 \times M_2$
, where we denote the base-changed versions of
$Y_2 \times M_2$
, where we denote the base-changed versions of
![]() $\phi, \Xi$
by the same symbol. By the second identity of Lemma 4.8, we have
$\phi, \Xi$
by the same symbol. By the second identity of Lemma 4.8, we have
This readily implies
![]() $\phi ^* T_{M_2}^{{\rm vir}} \cong T_{M_1}^{{\rm vir}}$
. Note that this reasoning does not require the universal sheaf
$\phi ^* T_{M_2}^{{\rm vir}} \cong T_{M_1}^{{\rm vir}}$
. Note that this reasoning does not require the universal sheaf
![]() $\mathcal{E}_1$
to exist globally on
$\mathcal{E}_1$
to exist globally on
![]() $Y_1 \times M_1$
. This equality, and Siebert’s formula [Reference SiebertSie04, Theorem 4.6], imply that the virtual classes defined by both moduli problems agree,Footnote
18
$Y_1 \times M_1$
. This equality, and Siebert’s formula [Reference SiebertSie04, Theorem 4.6], imply that the virtual classes defined by both moduli problems agree,Footnote
18
Note that it is not necessary to establish that
![]()
commutes, and we will therefore not do this.
To complete this part of the proof, we should check that the invariants themselves agree. Lemma 4.8 implies that
 \begin{align*} \pi _2^*\phi ^*(\mathcal{E}_2^{\otimes r} \otimes \det (\mathcal{E}_2)^{-1}) & \cong (\pi _2^* \phi ^*\mathcal{E}_2)^{\otimes r} \otimes \det (\pi _2^* \phi ^*\mathcal{E}_2)^{-1})\\ & \cong (\pi _2^*\Xi (\mathcal{E}_1))^{\otimes r} \otimes \det (\pi _2^*\Xi (\mathcal{E}_1))^{-1}\\ & \cong (\pi _1^*\mathcal{E}_1 \otimes L)^{\otimes r} \otimes \det (\pi _1^*\mathcal{E}_1 \otimes L)^{-1}\\ & \cong \pi _1^*( \mathcal{E}_1^{\otimes r} \otimes \det (\mathcal{E}_1)^{-1}). \end{align*}
\begin{align*} \pi _2^*\phi ^*(\mathcal{E}_2^{\otimes r} \otimes \det (\mathcal{E}_2)^{-1}) & \cong (\pi _2^* \phi ^*\mathcal{E}_2)^{\otimes r} \otimes \det (\pi _2^* \phi ^*\mathcal{E}_2)^{-1})\\ & \cong (\pi _2^*\Xi (\mathcal{E}_1))^{\otimes r} \otimes \det (\pi _2^*\Xi (\mathcal{E}_1))^{-1}\\ & \cong (\pi _1^*\mathcal{E}_1 \otimes L)^{\otimes r} \otimes \det (\pi _1^*\mathcal{E}_1 \otimes L)^{-1}\\ & \cong \pi _1^*( \mathcal{E}_1^{\otimes r} \otimes \det (\mathcal{E}_1)^{-1}). \end{align*}
Note that it is crucial that we work with the ‘normalized’ universal sheaves. This gives us that, for any
![]() $\alpha \in H^*(X, \mathbb{Q})$
and
$\alpha \in H^*(X, \mathbb{Q})$
and
![]() $k \in \mathbb{Z}$
, we have
$k \in \mathbb{Z}$
, we have
where
![]() $\pi _X : M_i \times X \to X$
is the projection. We conclude that, for any
$\pi _X : M_i \times X \to X$
is the projection. We conclude that, for any
![]() $\boldsymbol{a}$
,
$\boldsymbol{a}$
,
![]() $\boldsymbol{\alpha }$
as in Definition4.6, we have
$\boldsymbol{\alpha }$
as in Definition4.6, we have
 \begin{align*} \int _{[M_{Y_1,\xi /r}^H(r,\xi, c_2)]^{{\rm vir}}} \mathsf{P}_{{\rm vd}(r,\xi, c_2),\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M_{Y_1,\xi /r}^H(r,\xi, c_2),\mathcal{E}_1) \\ = \int _{[M_{Y_2,\xi /r}^H(r,\xi, c_2)]^{{\rm vir}}} \mathsf{P}_{{\rm vd}(r,\xi, c_2),\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M_{Y_2,\xi /r}^H(r,\xi, c_2),\mathcal{E}_2). \end{align*}
\begin{align*} \int _{[M_{Y_1,\xi /r}^H(r,\xi, c_2)]^{{\rm vir}}} \mathsf{P}_{{\rm vd}(r,\xi, c_2),\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M_{Y_1,\xi /r}^H(r,\xi, c_2),\mathcal{E}_1) \\ = \int _{[M_{Y_2,\xi /r}^H(r,\xi, c_2)]^{{\rm vir}}} \mathsf{P}_{{\rm vd}(r,\xi, c_2),\boldsymbol{a}}(r,X,\boldsymbol{\alpha };M_{Y_2,\xi /r}^H(r,\xi, c_2),\mathcal{E}_2). \end{align*}
The second part of the proposition follows [Reference Jiang and KoolJK21, Proposition 3.1]. Let
![]() $\pi : Y \rightarrow X$
be a degree
$\pi : Y \rightarrow X$
be a degree
![]() $r$
Brauer–Severi variety with
$r$
Brauer–Severi variety with
![]() $w(Y)=w$
and let
$w(Y)=w$
and let
![]() $\xi, \xi ^{\prime} \in H^2(X,\mathbb{Z})$
be two representatives of
$\xi, \xi ^{\prime} \in H^2(X,\mathbb{Z})$
be two representatives of
![]() $w$
(Lemma 3.1). Then
$w$
(Lemma 3.1). Then
![]() $\xi ^{\prime} = \xi +r\gamma$
for some
$\xi ^{\prime} = \xi +r\gamma$
for some
![]() $\gamma \in H^2(X,\mathbb{Z})$
. For any
$\gamma \in H^2(X,\mathbb{Z})$
. For any
![]() $Y$
-sheaf
$Y$
-sheaf
![]() $F$
we have
$F$
we have
if and only if
In particular,
![]() $M_{Y,\xi ^{\prime}/r}^H(r,\xi ^{\prime},c_2^{\prime}) = M_{Y,\xi /r}^H(r,\xi, c_2)$
and
$M_{Y,\xi ^{\prime}/r}^H(r,\xi ^{\prime},c_2^{\prime}) = M_{Y,\xi /r}^H(r,\xi, c_2)$
and
![]() ${\rm vd}(r,\xi ^{\prime},c_2^{\prime}) = {\rm vd}(r,\xi, c_2)$
. Summing over all
${\rm vd}(r,\xi ^{\prime},c_2^{\prime}) = {\rm vd}(r,\xi, c_2)$
. Summing over all
![]() $c_2$
,
$c_2$
,
![]() $c_2^{\prime}$
, the result follows.
$c_2^{\prime}$
, the result follows.
The independence of choice of
![]() $Y$
is perhaps not surprising, as this is just a particular model for the theory of twisted sheaves that we are using (although it is non-trivial that the Chern classes behave well under the equivalence discussed in Proposition 4.9). The independence of the choice of
$Y$
is perhaps not surprising, as this is just a particular model for the theory of twisted sheaves that we are using (although it is non-trivial that the Chern classes behave well under the equivalence discussed in Proposition 4.9). The independence of the choice of
![]() $\xi$
is also interesting: here we really need that we are dealing with generating functions and sum over all
$\xi$
is also interesting: here we really need that we are dealing with generating functions and sum over all
![]() $c_2$
. A different choice leads to a permutation of the terms of the generating function.
$c_2$
. A different choice leads to a permutation of the terms of the generating function.
We make some observations on the generating functions in Definitions4.5 and 4.6.
-
• The
 ${\rm SL}_r$
generating function is invariant under replacing
${\rm SL}_r$
generating function is invariant under replacing
 $\mathcal{E}$
by
$\mathcal{E}$
by
 $\mathcal{E} \otimes \mathcal{L}$
for any line bundle
$\mathcal{E} \otimes \mathcal{L}$
for any line bundle
 $\mathcal{L}$
on
$\mathcal{L}$
on
 $X \times M$
. Let
$X \times M$
. Let
 $L$
be a line bundle on
$L$
be a line bundle on
 $X$
and suppose
$X$
and suppose
 $- \otimes L$
preserves stability, i.e. it induces an isomorphismThis happens, for example, when (i)
$- \otimes L$
preserves stability, i.e. it induces an isomorphismThis happens, for example, when (i) \begin{align*} \bigsqcup _{c_2} M_{X}^H(r,c_1,c_2) \to \bigsqcup _{c_2} M_{X}^H(r,c_1+rc_1(L),c_2). \end{align*}
\begin{align*} \bigsqcup _{c_2} M_{X}^H(r,c_1,c_2) \to \bigsqcup _{c_2} M_{X}^H(r,c_1+rc_1(L),c_2). \end{align*}
 $L$
is a multiple of
$L$
is a multiple of
 $H$
, or (ii) when
$H$
, or (ii) when
 $\gcd (r,c_1H)=1$
so that Gieseker stability and
$\gcd (r,c_1H)=1$
so that Gieseker stability and
 $\mu$
-stability coincide [Reference Huybrechts and LehnHL10, Lemma 1.2.13, 1.2.14]. Then
$\mu$
-stability coincide [Reference Huybrechts and LehnHL10, Lemma 1.2.13, 1.2.14]. Then \begin{align*} \mathsf {Z}_{(X,H),c_1}^{\mathrm {SL}_r, \mathsf {P}}(q) = \mathsf {Z}_{(X,H),c_1+rc_1(L)}^{\mathrm {SL}_r, \mathsf {P}}(q). \end{align*}
\begin{align*} \mathsf {Z}_{(X,H),c_1}^{\mathrm {SL}_r, \mathsf {P}}(q) = \mathsf {Z}_{(X,H),c_1+rc_1(L)}^{\mathrm {SL}_r, \mathsf {P}}(q). \end{align*}
-
• Suppose
 $\alpha (Y) \in {\rm Br}(X)$
has order
$\alpha (Y) \in {\rm Br}(X)$
has order
 $r\gt 1$
. Then stability is automatic by Remark 3.5 and we write
$r\gt 1$
. Then stability is automatic by Remark 3.5 and we write \begin{align*} \mathsf {Z}_{X,w}^{\mathrm {PGL}_r, \mathsf {P}}(q) = \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {P}}(q). \end{align*}
\begin{align*} \mathsf {Z}_{X,w}^{\mathrm {PGL}_r, \mathsf {P}}(q) = \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {P}}(q). \end{align*}
-
• Many interesting virtual invariants can be obtained from appropriate choices of formal insertions
 $\mathsf{P}$
by the virtual Hirzebruch–Riemann–Roch theorem [Reference Ciocan-Fontanine and KapranovCFK09, Reference Fantechi and GöttscheFG10]:
$\mathsf{P}$
by the virtual Hirzebruch–Riemann–Roch theorem [Reference Ciocan-Fontanine and KapranovCFK09, Reference Fantechi and GöttscheFG10]:-
– virtual Euler characteristic
 $e^{{\rm vir}}$
, Hirzebruch genus
$e^{{\rm vir}}$
, Hirzebruch genus
 $\chi _{-y}^{{\rm vir}}$
, elliptic genus
$\chi _{-y}^{{\rm vir}}$
, elliptic genus
 $Ell^{{\rm vir}}$
. These were defined by Fantechi and Göttsche [Reference Fantechi and GöttscheFG10] and studied in the
$Ell^{{\rm vir}}$
. These were defined by Fantechi and Göttsche [Reference Fantechi and GöttscheFG10] and studied in the
 ${\rm SL}_r$
case in, e.g. [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b, Reference Göttsche, Kool and LaarakkerGKL24];
${\rm SL}_r$
case in, e.g. [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b, Reference Göttsche, Kool and LaarakkerGKL24]; -
– Donaldson invariants and
 $K$
-theoretic Donaldson invariants studied in algebraic geometry by Göttsche, Nakajima and Yoshioka in the
$K$
-theoretic Donaldson invariants studied in algebraic geometry by Göttsche, Nakajima and Yoshioka in the
 ${\rm SL}_r$
case in [Reference Göttsche, Nakajima and YoshiokaGNY11, Reference Göttsche, Nakajima and YoshiokaGNY08, Reference Göttsche, Nakajima and YoshiokaGNY09];
${\rm SL}_r$
case in [Reference Göttsche, Nakajima and YoshiokaGNY11, Reference Göttsche, Nakajima and YoshiokaGNY08, Reference Göttsche, Nakajima and YoshiokaGNY09]; -
– virtual cobordism class defined by Shen [Reference ShenShe16] and studied in the
 ${\rm SL}_r$
case in [Reference Göttsche and KoolGK19];
${\rm SL}_r$
case in [Reference Göttsche and KoolGK19]; -
– virtual Segre and Verlinde numbers [Reference Göttsche and KoolGK22, Reference Göttsche, Kool and WilliamsGKW21];
-
– Virasoro operators [Reference Bojko, Lim and MoreiraBLM24, Reference van BreevBr23].
-
We now make a comparison between moduli of sheaves on a trivial Brauer–Severi variety
![]() $\mathbb{P}(E^\vee ) \to X$
and moduli of sheaves on
$\mathbb{P}(E^\vee ) \to X$
and moduli of sheaves on
![]() $X$
.
$X$
.
Proposition 4.10.
Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
and consider a projective bundle
$H_1(X,\mathbb{Z}) = 0$
and consider a projective bundle
![]() $\pi : Y = \mathbb{P}(E^\vee ) \to X$
for a rank
$\pi : Y = \mathbb{P}(E^\vee ) \to X$
for a rank
![]() $r$
vector bundle
$r$
vector bundle
![]() $E$
on
$E$
on
![]() $X$
. Let
$X$
. Let
![]() $w := w(Y) \in H^2(X,\mu _r)$
and let
$w := w(Y) \in H^2(X,\mu _r)$
and let
![]() $c_1 \in H^2(X,\mathbb{Z})$
be a (necessarily algebraic) class representing
$c_1 \in H^2(X,\mathbb{Z})$
be a (necessarily algebraic) class representing
![]() $w$
. Suppose
$w$
. Suppose
![]() $\gcd (r,c_1 H)=1$
. Then there exists an isomorphism between Yoshioka and Gieseker–Maruyama–Simpson moduli spaces
$\gcd (r,c_1 H)=1$
. Then there exists an isomorphism between Yoshioka and Gieseker–Maruyama–Simpson moduli spaces
Moreover, under this isomorphism we have the following comparison of virtual fundamental classes and (normalized) universal sheaves: Footnote 19
 \begin{align*} \phi ^* T_{M_{X}^H(r,c_1,c_2)}^{{\rm vir}} \cong T_{M_{Y,c_1/r}^H(r,c_1,c_2)}^{{\rm vir}}, \quad \phi ^* [M_{X}^H(r,c_1,c_2)]^{{\rm vir}} & = [M_{Y,c_1/r}^H(r,c_1,c_2)]^{{\rm vir}}, \\ \pi ^* \phi ^* \Big ( (\mathcal{E}_2)^{\otimes r} \otimes \det (\mathcal{E}_2)^{-1} \Big ) \cong \mathcal{E}_1^{\otimes r} \otimes \det (\mathcal{E}_1)^{-1}, \end{align*}
\begin{align*} \phi ^* T_{M_{X}^H(r,c_1,c_2)}^{{\rm vir}} \cong T_{M_{Y,c_1/r}^H(r,c_1,c_2)}^{{\rm vir}}, \quad \phi ^* [M_{X}^H(r,c_1,c_2)]^{{\rm vir}} & = [M_{Y,c_1/r}^H(r,c_1,c_2)]^{{\rm vir}}, \\ \pi ^* \phi ^* \Big ( (\mathcal{E}_2)^{\otimes r} \otimes \det (\mathcal{E}_2)^{-1} \Big ) \cong \mathcal{E}_1^{\otimes r} \otimes \det (\mathcal{E}_1)^{-1}, \end{align*}
where
![]() $\pi$
and
$\pi$
and
![]() $\phi$
denote the appropriately base-changed morphisms.
$\phi$
denote the appropriately base-changed morphisms.
Proof. There exists an equivalence of categories [Reference YoshiokaYos06, Lemma 1.7]
We fix the
![]() $B$
-field
$B$
-field
![]() $\xi :=c_1$
. Using
$\xi :=c_1$
. Using
![]() $G = \pi ^*E(1)$
and the projection formula, a direct calculation shows that for any
$G = \pi ^*E(1)$
and the projection formula, a direct calculation shows that for any
![]() $Y$
-sheaf
$Y$
-sheaf
![]() $F$
, we have
$F$
, we have
Hence
![]() ${{\rm rk}}(F) ={{\rm rk}}(\Xi (F))$
. Suppose this rank is positive. Then, using the Hirzebruch–Riemann–Roch theorem, we find that the reduced Hilbert polynomials are related by
${{\rm rk}}(F) ={{\rm rk}}(\Xi (F))$
. Suppose this rank is positive. Then, using the Hirzebruch–Riemann–Roch theorem, we find that the reduced Hilbert polynomials are related by
 \begin{align*} {\chi (\pi _*(F \otimes G^\vee )(mH)) \over a_2^G(F)} = & {\chi (\Xi (F)(mH)) \over a_2(\Xi (F))} + {c_1(E^\vee )H \over r H^2} m \\ & + {c_1(E^\vee )c_1(X) \over 2rH^2} + {{\rm ch_2}(E^\vee ) \over r H^2} + {c_1(E^\vee )c_1(\Xi (F)) \over r{{\rm rk}}(\Xi (F)) H^2}. \end{align*}
\begin{align*} {\chi (\pi _*(F \otimes G^\vee )(mH)) \over a_2^G(F)} = & {\chi (\Xi (F)(mH)) \over a_2(\Xi (F))} + {c_1(E^\vee )H \over r H^2} m \\ & + {c_1(E^\vee )c_1(X) \over 2rH^2} + {{\rm ch_2}(E^\vee ) \over r H^2} + {c_1(E^\vee )c_1(\Xi (F)) \over r{{\rm rk}}(\Xi (F)) H^2}. \end{align*}
We would like to prove the following claim: for any torsion free sheaf
![]() $F$
on
$F$
on
![]() $X$
, we have
$X$
, we have
for any subsheaf
![]() $0 \neq F^{\prime} \subsetneq F$
, if and only if
$0 \neq F^{\prime} \subsetneq F$
, if and only if
![]() $F$
is
$F$
is
![]() $\mu$
-stable [Reference Huybrechts and LehnHL10, Definition 1.2.12]. We may replace
$\mu$
-stable [Reference Huybrechts and LehnHL10, Definition 1.2.12]. We may replace
![]() $\mathbb{P}(E^\vee )$
by
$\mathbb{P}(E^\vee )$
by
![]() $\mathbb{P}(E^\vee \otimes \mathcal{L}^N)$
, where
$\mathbb{P}(E^\vee \otimes \mathcal{L}^N)$
, where
![]() $\mathcal{L}$
is an ample line bundle on
$\mathcal{L}$
is an ample line bundle on
![]() $X$
and
$X$
and
![]() $N \in \mathbb{Z}_{\gt 0}$
. This replaces
$N \in \mathbb{Z}_{\gt 0}$
. This replaces
![]() $c_1(E^\vee )$
by
$c_1(E^\vee )$
by
![]() $N r c_1(\mathcal{L}) + c_1(E^\vee )$
which is ample for
$N r c_1(\mathcal{L}) + c_1(E^\vee )$
which is ample for
![]() $N \gg 0$
. In other words, we may assume
$N \gg 0$
. In other words, we may assume
![]() $E$
is chosen such that
$E$
is chosen such that
![]() $c_1(E^\vee )$
is ample. In particular, for any torsion free sheaf
$c_1(E^\vee )$
is ample. In particular, for any torsion free sheaf
![]() $F$
on
$F$
on
![]() $X$
and subsheaf
$X$
and subsheaf
![]() $F^{\prime}$
with
$F^{\prime}$
with
![]() ${{\rm rk}}(F^{\prime}) ={{\rm rk}}(F)$
, we have
${{\rm rk}}(F^{\prime}) ={{\rm rk}}(F)$
, we have
by the Nakai–Moishezon criterion. Assuming
![]() $\gcd ({{\rm rk}}(F),c_1(F) H)=1$
, the claim then easily follows. We deduce that
$\gcd ({{\rm rk}}(F),c_1(F) H)=1$
, the claim then easily follows. We deduce that
![]() $\Xi$
induces an isomorphism of moduli spacesFootnote
20
$\Xi$
induces an isomorphism of moduli spacesFootnote
20
The second part of the proposition is established exactly as in the proof of Proposition 4.9.
4.3 Deformation invariance
Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
. We pick a class
$H_1(X,\mathbb{Z}) = 0$
. We pick a class
![]() $w \in H^2(X,\mu _r)$
, a sequence of formal insertions
$w \in H^2(X,\mu _r)$
, a sequence of formal insertions
![]() $\mathsf{P}$
, and we consider the generating function
$\mathsf{P}$
, and we consider the generating function
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{P}}(q)$
. We will now show that this generating function is invariant under deformations of
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{P}}(q)$
. We will now show that this generating function is invariant under deformations of
![]() $(X,H)$
.
$(X,H)$
.
Let
![]() $f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
$f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension 2 with connected fibres over a smooth connected variety
![]() $B$
. Suppose that one fibre (and hence all fibres)
$B$
. Suppose that one fibre (and hence all fibres)
![]() $\mathcal{X}_b$
satisfies
$\mathcal{X}_b$
satisfies
![]() $H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. We fix a family of polarizations
$H_1(\mathcal{X}_b,\mathbb{Z}) = 0$
. We fix a family of polarizations
![]() $\mathcal{H}$
on
$\mathcal{H}$
on
![]() $\mathcal{X}$
. We consider
$\mathcal{X}$
. We consider
![]() $\mu _r \subset \mathcal{O}_{\mathcal{X}}^{\times }$
as a constructible sheaf in the étale topology on
$\mu _r \subset \mathcal{O}_{\mathcal{X}}^{\times }$
as a constructible sheaf in the étale topology on
![]() $\mathcal{X}$
. Then
$\mathcal{X}$
. Then
![]() $R^2 f_* \mu _r$
is a constructible sheaf too and
$R^2 f_* \mu _r$
is a constructible sheaf too and
for all closed points
![]() $b \in \mathcal{X}$
by the proper base change theorem [Reference MilneMil13, Theorem 17.7]. We fix a section
$b \in \mathcal{X}$
by the proper base change theorem [Reference MilneMil13, Theorem 17.7]. We fix a section
Given a class
![]() $w \in H^2(\mathcal{X}_b, \mu _r)$
for some closed point
$w \in H^2(\mathcal{X}_b, \mu _r)$
for some closed point
![]() $b \in B$
, it is always possible to find such
$b \in B$
, it is always possible to find such
![]() $\widetilde{w}$
in an étale neighbourhood of
$\widetilde{w}$
in an étale neighbourhood of
![]() $b$
that restricts to
$b$
that restricts to
![]() $w$
over
$w$
over
![]() $b$
. This fact uses the proper base change theorem. We make the following two assumptions:
$b$
. This fact uses the proper base change theorem. We make the following two assumptions:
-
•
 $r$
is prime; and
$r$
is prime; and -
•
 $\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
$\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
 $b \in B$
.
$b \in B$
.
This allows us to rule out strictly semistable objects as follows.
Lemma 4.11.
Suppose
![]() $r$
is prime and
$r$
is prime and
![]() $\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
$\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. Then, for any closed point
$b \in B$
. Then, for any closed point
![]() $b \in B$
, any degree
$b \in B$
, any degree
![]() $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
![]() $Y \to \mathcal{X}_b$
with
$Y \to \mathcal{X}_b$
with
![]() $w(Y) = \widetilde{w}_b$
, and any
$w(Y) = \widetilde{w}_b$
, and any
![]() $c_2$
, the moduli space
$c_2$
, the moduli space
![]() $M_{Y}^{\mathcal{H}_b}(r,0,c_2)$
is projective.
$M_{Y}^{\mathcal{H}_b}(r,0,c_2)$
is projective.
Proof.
Since
![]() $r$
is prime, the order of the Brauer class
$r$
is prime, the order of the Brauer class
![]() $o(\widetilde{w}_{b}) \in {\rm Br}(\mathcal{X}_b)$
is either
$o(\widetilde{w}_{b}) \in {\rm Br}(\mathcal{X}_b)$
is either
![]() $r$
or
$r$
or
![]() $1$
. In the former case, there are no strictly semistable objects because stability is automatic (Remark 3.5). In the latter case, we apply Proposition 4.10.Footnote
21
$1$
. In the former case, there are no strictly semistable objects because stability is automatic (Remark 3.5). In the latter case, we apply Proposition 4.10.Footnote
21
We require the following result of de Jong used in his proof of the period-index theorem [Reference de JongdJo04] (and which does not require
![]() $r$
prime):Footnote
22
$r$
prime):Footnote
22
Theorem 4.12. (de Jong). For any closed point
![]() $0 \in B$
, there exists an étale neighbourhood
$0 \in B$
, there exists an étale neighbourhood
![]() $(U,0) \to (B,0)$
and a degree
$(U,0) \to (B,0)$
and a degree
![]() $r$
Azumaya algebra
$r$
Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $\mathcal{X}_{U} := \mathcal{X} \times _B U$
such that
$\mathcal{X}_{U} := \mathcal{X} \times _B U$
such that
for all closed points
![]() $b \in U$
.
$b \in U$
.
The idea of the proof of this result is as follows. Pick a closed point
![]() $0 \in B$
. By Theorem 2.15 (which is actually a consequence of the period-index theorem [Reference LieblichLie08]), there exists an Azumaya algebra
$0 \in B$
. By Theorem 2.15 (which is actually a consequence of the period-index theorem [Reference LieblichLie08]), there exists an Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
such that
$X$
such that
![]() $w(\mathcal{A}) = \widetilde{w}_0 \in H^2(\mathcal{X}_0,\mu _r)$
. The obstruction space governing deformations of
$w(\mathcal{A}) = \widetilde{w}_0 \in H^2(\mathcal{X}_0,\mu _r)$
. The obstruction space governing deformations of
![]() $\mathcal{A}$
is given by
$\mathcal{A}$
is given by
![]() $H^2(\mathcal{X}_0,\mathcal{A} / \mathcal{O}_{\mathcal{X}_0})$
. de Jong shows that (after applying an elementary transformation to
$H^2(\mathcal{X}_0,\mathcal{A} / \mathcal{O}_{\mathcal{X}_0})$
. de Jong shows that (after applying an elementary transformation to
![]() $\mathcal{A}$
), we may choose
$\mathcal{A}$
), we may choose
![]() $\mathcal{A}$
such that
$\mathcal{A}$
such that
![]() $H^2(\mathcal{X}_0,\mathcal{A} / \mathcal{O}_{\mathcal{X}_0}) = 0$
[Reference de JongdJo04, Proposition 3.2]. Using Grothendieck’s existence theorem and Artin’s approximation theorem, it then follows that there exists an étale neighbourhood
$H^2(\mathcal{X}_0,\mathcal{A} / \mathcal{O}_{\mathcal{X}_0}) = 0$
[Reference de JongdJo04, Proposition 3.2]. Using Grothendieck’s existence theorem and Artin’s approximation theorem, it then follows that there exists an étale neighbourhood
![]() $U \to B$
and a degree
$U \to B$
and a degree
![]() $r$
Azumaya algebra
$r$
Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $\mathcal{X}_{U} := \mathcal{X} \times _B U$
such that
$\mathcal{X}_{U} := \mathcal{X} \times _B U$
such that
![]() $w(\mathcal{A}_0) = \widetilde{w}_0$
. Using the proper base change theorem, we can go to a further étale neighbourhood where
$w(\mathcal{A}_0) = \widetilde{w}_0$
. Using the proper base change theorem, we can go to a further étale neighbourhood where
![]() $w(\mathcal{A}_b) = \widetilde{w}_b$
for all closed points
$w(\mathcal{A}_b) = \widetilde{w}_b$
for all closed points
![]() $b \in U$
.
$b \in U$
.
For the following theorem, we fix
![]() $\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
and a family of formal insertions
$\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
and a family of formal insertions
![]() $\mathsf{P} = \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
(§ 4.2). Furthermore, for each
$\mathsf{P} = \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
(§ 4.2). Furthermore, for each
![]() $i=1, \ldots, N$
, we fix a flat section
$i=1, \ldots, N$
, we fix a flat section
We suppose
![]() $r$
is prime and
$r$
is prime and
![]() $\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
$\gcd (r, \widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. By Lemma 4.11, the
$b \in B$
. By Lemma 4.11, the
![]() ${\rm PGL}_r$
generating function
${\rm PGL}_r$
generating function
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is defined on all the fibres of
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is defined on all the fibres of
![]() $\mathcal{X} \to B$
.
$\mathcal{X} \to B$
.
Theorem 4.13.
Let
![]() $\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
$\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
![]() $r$
is prime and
$r$
is prime and
![]() ${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. Then
$b \in B$
. Then
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of the closed point
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of the closed point
![]() $b \in B$
.
$b \in B$
.
Proof.
First, fix a closed point
![]() $b \in \mathcal{B}$
and let
$b \in \mathcal{B}$
and let
![]() $X := \mathcal{X}_b$
,
$X := \mathcal{X}_b$
,
![]() $H:=\mathcal{H}_b$
,
$H:=\mathcal{H}_b$
,
![]() $w := \widetilde{w}_b$
, and
$w := \widetilde{w}_b$
, and
![]() $\alpha _i := (\widetilde{\alpha }_i)_b$
for all
$\alpha _i := (\widetilde{\alpha }_i)_b$
for all
![]() $i$
. As discussed in Remark 4.4, it is not desirable to extend the
$i$
. As discussed in Remark 4.4, it is not desirable to extend the
![]() $B$
-field in families, so we first observe
$B$
-field in families, so we first observe
We focus on deformation invariance of the term indexed by
![]() $c_2 \in \mathbb{Q}$
in the generating function. Note that
$c_2 \in \mathbb{Q}$
in the generating function. Note that
![]() ${{\rm ch}} = (r,0,-c_2)$
trivially extends to a flat section
${{\rm ch}} = (r,0,-c_2)$
trivially extends to a flat section
![]() $\widetilde{v} \in \bigoplus _{p} \Gamma (B, \mathcal{H}^{2p}_{{\rm dR}})$
.
$\widetilde{v} \in \bigoplus _{p} \Gamma (B, \mathcal{H}^{2p}_{{\rm dR}})$
.
By Theorem 4.12, we can cover the base
![]() $B$
by (connected) étale opens
$B$
by (connected) étale opens
![]() $U \to B$
, such that on each
$U \to B$
, such that on each
![]() $\mathcal{X}_U \to U$
, we have an Azumaya algebras
$\mathcal{X}_U \to U$
, we have an Azumaya algebras
![]() $\mathcal{A}$
of degree
$\mathcal{A}$
of degree
![]() $r$
with
$r$
with
![]() $w(\mathcal{A}_b) = \widetilde{w}_b$
for all
$w(\mathcal{A}_b) = \widetilde{w}_b$
for all
![]() $b \in U$
. Fix such an open. By the correspondence of Proposition 2.5, we therefore have a family of degree
$b \in U$
. Fix such an open. By the correspondence of Proposition 2.5, we therefore have a family of degree
![]() $r$
Brauer–Severi varieties
$r$
Brauer–Severi varieties
such that
![]() $w(\mathcal{Y}_U|_b) = \widetilde{w}_b$
for all
$w(\mathcal{Y}_U|_b) = \widetilde{w}_b$
for all
![]() $b \in U$
. Hence, we have a relative moduli space
$b \in U$
. Hence, we have a relative moduli space
![]() $M_{\mathcal{Y}_U/\mathcal{X}_U}$
and virtual fundamental class
$M_{\mathcal{Y}_U/\mathcal{X}_U}$
and virtual fundamental class
![]() $[M_{\mathcal{Y}_U/\mathcal{X}_U}]^{{\rm vir}}$
as in § 4.1. Since
$[M_{\mathcal{Y}_U/\mathcal{X}_U}]^{{\rm vir}}$
as in § 4.1. Since
![]() $\mathsf{P}$
lifts to an insertion on
$\mathsf{P}$
lifts to an insertion on
![]() $M_{\mathcal{Y}_U/\mathcal{X}_U}$
, we deduce from (12) that the term corresponding to
$M_{\mathcal{Y}_U/\mathcal{X}_U}$
, we deduce from (12) that the term corresponding to
![]() $c_2$
of
$c_2$
of
![]() $\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of
$\mathsf{Z}_{(\mathcal{X}_{b},\mathcal{H}_{b}),\widetilde{w}_{b}}^{{\rm PGL}_r, \mathsf{P}}(q)$
is independent of
![]() $b$
in the image of
$b$
in the image of
![]() $U \to B$
.
$U \to B$
.
5. The
 ${\rm PGL}_r$
–
${\rm PGL}_r$
–
 ${\rm SL}_r$
correspondence
${\rm SL}_r$
correspondence
5.1 Main result
Let
![]() $f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension
$f : \mathcal{X} \to B$
be a smooth projective morphism of relative dimension
![]() $n$
with connected fibres over a smooth connected variety
$n$
with connected fibres over a smooth connected variety
![]() $B$
. We first let the relative dimension
$B$
. We first let the relative dimension
![]() $n$
be arbitrary. Suppose
$n$
be arbitrary. Suppose
![]() $H_1(\mathcal{X}_b,\mathbb{Z})_{{\rm tor}} = 0$
for some (and hence all) closed points
$H_1(\mathcal{X}_b,\mathbb{Z})_{{\rm tor}} = 0$
for some (and hence all) closed points
![]() $b \in B$
. We recall that the stalk of the constructible sheaf
$b \in B$
. We recall that the stalk of the constructible sheaf
![]() $R^2 f_* \mu _r$
at
$R^2 f_* \mu _r$
at
![]() $b$
is
$b$
is
by the proper base change theorem. We fix a section
We will now work in the complex analytic topology and make the following assumption: there exists a closed point
![]() $0 \in B$
and a class
$0 \in B$
and a class
![]() $\beta \in H^{1,1}(\mathcal{X}_0)$
such that the composition
$\beta \in H^{1,1}(\mathcal{X}_0)$
such that the composition
is surjective. Here the first map is the Kodaira–Spencer map, the second map is
![]() $\cup \beta$
and the final map is contraction.
$\cup \beta$
and the final map is contraction.
By [Reference Voisin, Farkas and MorrisonVoi13, Reference VoisinVoi03], this map can also be expressed in terms of the Gauß–Manin connection
as
![]() $\overline{\nabla }_0(\beta )$
, where
$\overline{\nabla }_0(\beta )$
, where
![]() $\beta$
is viewed as an element of
$\beta$
is viewed as an element of
![]() $(F^1 \mathcal{H}^2_{{\rm dR}} / F^2 \mathcal{H}^2_{{\rm dR}})|_0$
. The surjectivity of (15) implies that the Noether–Lefschetz locus of
$(F^1 \mathcal{H}^2_{{\rm dR}} / F^2 \mathcal{H}^2_{{\rm dR}})|_0$
. The surjectivity of (15) implies that the Noether–Lefschetz locus of
![]() $\beta$
, i.e. locally analytically the locus in
$\beta$
, i.e. locally analytically the locus in
![]() $B$
where
$B$
where
![]() $\beta$
remains of Hodge type
$\beta$
remains of Hodge type
![]() $(1,1)$
, is smooth of ‘expected’ codimension
$(1,1)$
, is smooth of ‘expected’ codimension
![]() $h^{2,0}(\mathcal{X}_0)$
at
$h^{2,0}(\mathcal{X}_0)$
at
![]() $0$
[Reference Voisin, Farkas and MorrisonVoi13]. Precisely the same assumption is made by Green to show that the Hodge locus is dense [Reference GreenGre89]. When
$0$
[Reference Voisin, Farkas and MorrisonVoi13]. Precisely the same assumption is made by Green to show that the Hodge locus is dense [Reference GreenGre89]. When
![]() $n=2$
and
$n=2$
and
![]() $\beta$
is Poincaré dual to an algebraic class on
$\beta$
is Poincaré dual to an algebraic class on
![]() $\mathcal{X}_0$
, the same assumption is also used in the theory of reduced virtual fundamental classes in [Reference Kool and ThomasKT14a, Reference Kool and ThomasKT14b]. Note that
$\mathcal{X}_0$
, the same assumption is also used in the theory of reduced virtual fundamental classes in [Reference Kool and ThomasKT14a, Reference Kool and ThomasKT14b]. Note that
![]() $\beta$
does not have to be related to
$\beta$
does not have to be related to
![]() $\widetilde{w}$
; all we require is the existence of some class with Noether–Lefschetz locus of expected codimension.
$\widetilde{w}$
; all we require is the existence of some class with Noether–Lefschetz locus of expected codimension.
Example 5.1. The family
![]() $\mathcal{X} \to B \subset |\mathcal{O}_{\mathbb{P}^3}(d)|$
of smooth degree
$\mathcal{X} \to B \subset |\mathcal{O}_{\mathbb{P}^3}(d)|$
of smooth degree
![]() $d$
surfaces in
$d$
surfaces in
![]() $\mathbb{P}^3$
of degree
$\mathbb{P}^3$
of degree
![]() $d \geq 4$
has the property that the locus of points in
$d \geq 4$
has the property that the locus of points in
![]() $B$
admitting
$B$
admitting
![]() $\beta$
, such that (15) is surjective, is dense by [Reference KimKim91] (see also [Reference Ciliberto, Harris and MirandaCHM88]).
$\beta$
, such that (15) is surjective, is dense by [Reference KimKim91] (see also [Reference Ciliberto, Harris and MirandaCHM88]).
Example 5.2. Let
![]() $U$
be the moduli space of relatively minimal elliptic surfaces
$U$
be the moduli space of relatively minimal elliptic surfaces
![]() $X \to \mathbb{P}^1$
with a section, irregularity
$X \to \mathbb{P}^1$
with a section, irregularity
![]() $q=0$
, and geometric genus
$q=0$
, and geometric genus
![]() $p_g \geq 2$
. Suppose that
$p_g \geq 2$
. Suppose that
![]() $X$
is an elliptic surface which has no reducible fibres and
$X$
is an elliptic surface which has no reducible fibres and
![]() $j$
-invariant not identically zero. Then [Reference CoxCox90, Proposition 1.18] calculates the rank of (15). Using this description, one can find classes
$j$
-invariant not identically zero. Then [Reference CoxCox90, Proposition 1.18] calculates the rank of (15). Using this description, one can find classes
![]() $\beta$
satisfying (15).
$\beta$
satisfying (15).
For further examples, we also refer to [Reference Bruzzo, Grassi and LopezBGL21].
Proposition 5.3.
Suppose
(15)
is surjective. For any complex analytic simply connected neighbourhood
![]() $U$
of
$U$
of
![]() $0 \in B$
, there exists a point
$0 \in B$
, there exists a point
![]() $b \in U$
such that the Brauer class of
$b \in U$
such that the Brauer class of
![]() $\widetilde{w}_{b}$
is trivial.
$\widetilde{w}_{b}$
is trivial.
Proof.
As in [Reference VoisinVoi03, Proposition 5.20], we first observe that (15) is a Zariski open condition on
![]() $\beta$
, so we may take
$\beta$
, so we may take
![]() $\beta \in H^{1,1}(\mathcal{X}_0) \cap H^2(\mathcal{X}_0, \mathbb{R})$
. Take any simply connected open neighbourhood
$\beta \in H^{1,1}(\mathcal{X}_0) \cap H^2(\mathcal{X}_0, \mathbb{R})$
. Take any simply connected open neighbourhood
![]() $U$
of
$U$
of
![]() $0$
. Using the notation of [Reference VoisinVoi03], we have a trivialization
$0$
. Using the notation of [Reference VoisinVoi03], we have a trivialization
and (on
![]() $U$
) we consider the composition
$U$
) we consider the composition
where
![]() $\pi$
is the projection. Surjectivity of (15) implies that this map is a submersion at
$\pi$
is the projection. Surjectivity of (15) implies that this map is a submersion at
![]() $(0,\beta )$
by [Reference VoisinVoi03, Lemma 5.22], and hence a submersion in a neighbourhood
$(0,\beta )$
by [Reference VoisinVoi03, Lemma 5.22], and hence a submersion in a neighbourhood
![]() $W$
of
$W$
of
![]() $(0,\beta )$
. In particular
$(0,\beta )$
. In particular
![]() $\phi$
is open on
$\phi$
is open on
![]() $W$
. We note that
$W$
. We note that
![]() $t$
preserves rational and integral classes. Furthermore, viewing
$t$
preserves rational and integral classes. Furthermore, viewing
![]() $R^2 f_* \mu _r$
as a local system in the complex analytic topology,Footnote
23
$R^2 f_* \mu _r$
as a local system in the complex analytic topology,Footnote
23
![]() $t$
trivializes
$t$
trivializes
![]() $R^2f_* \mu _r|_U$
to the constant sheaf
$R^2f_* \mu _r|_U$
to the constant sheaf
![]() $H^2(\mathcal{X}_0,\mu _r)$
.
$H^2(\mathcal{X}_0,\mu _r)$
.
Still working over
![]() $U$
, since
$U$
, since
![]() $H^2(\mathcal{X}_0,\mathbb{Q})$
is dense in
$H^2(\mathcal{X}_0,\mathbb{Q})$
is dense in
![]() $H^2(\mathcal{X}_0,\mathbb{R})$
we can pick a
$H^2(\mathcal{X}_0,\mathbb{R})$
we can pick a
![]() $(b^{\prime},\gamma ) \in W$
with
$(b^{\prime},\gamma ) \in W$
with
![]() $\pi (t(b^{\prime},\gamma ))$
rational, and hence
$\pi (t(b^{\prime},\gamma ))$
rational, and hence
![]() $\gamma$
rational. Now choose a representative
$\gamma$
rational. Now choose a representative
![]() $\xi \in H^2(\mathcal{X}_0,\mathbb{Z})$
of
$\xi \in H^2(\mathcal{X}_0,\mathbb{Z})$
of
![]() $\widetilde{w}_0$
(Lemma 3.1). Consider the class
$\widetilde{w}_0$
(Lemma 3.1). Consider the class
for any
![]() $N \in \mathbb{Z}_{\gt 0}$
. Using the fact that
$N \in \mathbb{Z}_{\gt 0}$
. Using the fact that
![]() $\phi$
is open in a neighbourhood of
$\phi$
is open in a neighbourhood of
![]() $(b^{\prime},\gamma )$
, we can choose
$(b^{\prime},\gamma )$
, we can choose
![]() $N \gg 0$
such that
$N \gg 0$
such that
![]() $\pi (t(b^{\prime},\gamma )) + \xi / rN$
lies in the image of
$\pi (t(b^{\prime},\gamma )) + \xi / rN$
lies in the image of
![]() $\phi$
and such that
$\phi$
and such that
![]() $N \pi (t(b^{\prime},\gamma ))$
is integral. Then there exists a
$N \pi (t(b^{\prime},\gamma ))$
is integral. Then there exists a
![]() $(b,\delta ) \in \mathcal{H}_{\mathbb{R}}^{1,1}$
mapping to
$(b,\delta ) \in \mathcal{H}_{\mathbb{R}}^{1,1}$
mapping to
![]() $\pi (t(b^{\prime},\gamma )) + \xi / rN$
. Since
$\pi (t(b^{\prime},\gamma )) + \xi / rN$
. Since
![]() $t$
preserves rational and integral classes, we deduce that
$t$
preserves rational and integral classes, we deduce that
![]() $\epsilon :=rN \delta$
is an integral
$\epsilon :=rN \delta$
is an integral
![]() $(1,1)$
class on
$(1,1)$
class on
![]() $\mathcal{X}_{b}$
. Moreover,
$\mathcal{X}_{b}$
. Moreover,
![]() $\epsilon \mod r H^2(\mathcal{X}_{b},\mathbb{Z})$
corresponds to
$\epsilon \mod r H^2(\mathcal{X}_{b},\mathbb{Z})$
corresponds to
![]() $\xi \mod r H^2(\mathcal{X}_{0},\mathbb{Z})$
. Hence
$\xi \mod r H^2(\mathcal{X}_{0},\mathbb{Z})$
. Hence
![]() $\epsilon$
represents
$\epsilon$
represents
![]() $\widetilde{w}_{b}$
, and
$\widetilde{w}_{b}$
, and
![]() $\widetilde{w}_{b}$
has trivial Brauer class by the Kummer sequence (5).
$\widetilde{w}_{b}$
has trivial Brauer class by the Kummer sequence (5).
We now come to the main theorem of the paper. We fix the relative dimension of
![]() $f : \mathcal{X} \to B$
to be 2. We also choose a relative very ample divisor
$f : \mathcal{X} \to B$
to be 2. We also choose a relative very ample divisor
![]() $\mathcal{H}$
with respect to
$\mathcal{H}$
with respect to
![]() $f$
. Over some closed point
$f$
. Over some closed point
![]() $0 \in B$
, we fix a Stiefel–Whitney class
$0 \in B$
, we fix a Stiefel–Whitney class
We fix
![]() $\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
and a family of formal insertions
$\boldsymbol{a} = (a_1, \ldots, a_N) \in \{1,2\}^N$
and a family of formal insertions
![]() $\mathsf{P} = \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
(§ 4.2). Furthermore, for each
$\mathsf{P} = \{\mathsf{P}_{v,\boldsymbol{a}}\}_{v \geq 0}$
(§ 4.2). Furthermore, for each
![]() $i=1, \ldots, N$
, we fix an algebraic class
$i=1, \ldots, N$
, we fix an algebraic class
By the proper base change theorem, after replacing
![]() $B$
by an étale neighbourhood of
$B$
by an étale neighbourhood of
![]() $0$
, we may assume that
$0$
, we may assume that
![]() $w$
extends to a section
$w$
extends to a section
By base change for Hodge bundles, after replacing
![]() $B$
by a Zariski neighbourhood of
$B$
by a Zariski neighbourhood of
![]() $0$
, we may assume the classes
$0$
, we may assume the classes
![]() $\alpha _i$
extend to flat sections
$\alpha _i$
extend to flat sections
Theorem 5.4.
Let
![]() $\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
$\widetilde{w} \in H^0(B,R^2 f_* \mu _r)$
be a section. Suppose
![]() $r$
is prime and
$r$
is prime and
![]() ${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
${\rm gcd}(r,\widetilde{w}_b \mathcal{H}_b)=1$
for some (and hence all) closed points
![]() $b \in B$
. Suppose for some closed point
$b \in B$
. Suppose for some closed point
![]() $0 \in B$
, there exists a class
$0 \in B$
, there exists a class
![]() $\beta \in H^{1,1}(\mathcal{X}_0)$
such that the following composition is surjective:
$\beta \in H^{1,1}(\mathcal{X}_0)$
such that the following composition is surjective:
where the first arrow is the Kodaira–Spencer map and the second is cupping with
![]() $\beta$
followed by contraction. Then any complex analytic simply connected neighbourhood
$\beta$
followed by contraction. Then any complex analytic simply connected neighbourhood
![]() $U$
of
$U$
of
![]() $0$
contains a closed point
$0$
contains a closed point
![]() $b \in U$
such that
$b \in U$
such that
![]() $\widetilde{w}_{b} \in H^2(\mathcal{X}_{b},\mu _r)$
has trivial Brauer class and
$\widetilde{w}_{b} \in H^2(\mathcal{X}_{b},\mu _r)$
has trivial Brauer class and
where
![]() $c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
is any (necessarily algebraic) representative of
$c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
is any (necessarily algebraic) representative of
![]() $\widetilde{w}_{b}$
.
$\widetilde{w}_{b}$
.
Proof.
Let
![]() $U$
be any complex analytic simply connected neighbourhood of
$U$
be any complex analytic simply connected neighbourhood of
![]() $0$
. By Proposition 5.3, there exists a closed point
$0$
. By Proposition 5.3, there exists a closed point
![]() $b \in U$
such that
$b \in U$
such that
![]() $\widetilde{w}_{b}$
has trivial Brauer class. By Theorem 4.13, we have
$\widetilde{w}_{b}$
has trivial Brauer class. By Theorem 4.13, we have
Pick a (necessarily algebraic) representative
![]() $c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
of
$c_1 \in H^2(\mathcal{X}_{b},\mathbb{Z})$
of
![]() $\widetilde{w}_{b}$
(Lemma 3.1, (5)). Pick a degree
$\widetilde{w}_{b}$
(Lemma 3.1, (5)). Pick a degree
![]() $r$
Brauer–Severi variety over
$r$
Brauer–Severi variety over
![]() $\mathcal{X}_b$
with Stiefel–Whitney class
$\mathcal{X}_b$
with Stiefel–Whitney class
![]() $\widetilde{w}_{b}$
(Theorem 2.16), which is therefore of the form
$\widetilde{w}_{b}$
(Theorem 2.16), which is therefore of the form
![]() $\mathbb{P}(E^\vee )$
for a rank
$\mathbb{P}(E^\vee )$
for a rank
![]() $r$
vector bundle
$r$
vector bundle
![]() $E$
on
$E$
on
![]() $\mathcal{X}_b$
(§ 2.1). By Proposition 4.10, we have
$\mathcal{X}_b$
(§ 2.1). By Proposition 4.10, we have
which establishes the result.
5.2 Application to Vafa–Witten theory
We recall the ‘horizontal’ universality conjecture of the fourth-named author and Göttsche and Laarakker [Reference Göttsche, Kool and LaarakkerGKL24, Conjecture 1.10]. We defined
![]() $\overline{\Delta }(q)$
and
$\overline{\Delta }(q)$
and
![]() $\epsilon _r$
in the introduction.
$\epsilon _r$
in the introduction.
Conjecture 5.5. (Göttsche–Kool–Laarakker). For any
![]() $r\gt 1$
, there exist
Footnote
24
$r\gt 1$
, there exist
Footnote
24
with the following property. For any smooth polarized surface
![]() $(X,H)$
satisfying
$(X,H)$
satisfying
![]() $b_1(X)=0$
,
$b_1(X)=0$
,
![]() $h^{2,0}(X)\gt 0$
,
$h^{2,0}(X)\gt 0$
,
![]() $c_1 \in H^2(X,\mathbb{Z})$
, and
$c_1 \in H^2(X,\mathbb{Z})$
, and
![]() $c_2 \in H^4(X,\mathbb{Z})$
such that there are no rank
$c_2 \in H^4(X,\mathbb{Z})$
such that there are no rank
![]() $r$
strictly Gieseker
$r$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with Chern classes
$X$
with Chern classes
![]() $c_1,c_2$
, the virtual Euler characteristic
$c_1,c_2$
, the virtual Euler characteristic
![]() $e^{{\rm vir}}(M_X^H(r,c_1,c_2))$
equals the coefficient of
$e^{{\rm vir}}(M_X^H(r,c_1,c_2))$
equals the coefficient of
![]() $q^{{\rm vd}(r,c_1,c_2)/2r}$
in
$q^{{\rm vd}(r,c_1,c_2)/2r}$
in
 \begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i c_1} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
\begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i c_1} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
Evidence for this conjecture was obtained by direct implementation of Mochizuki’s formula [Reference MochizukiMoc09] in [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b]. We deduce the following.
Corollary 5.6.
Suppose
![]() $X = \mathcal{X}_0$
and
$X = \mathcal{X}_0$
and
![]() $w = \widetilde{w}_0$
for a family
$w = \widetilde{w}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4 and
$\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4 and
![]() $h^{2,0}(X)\gt 0$
. Fix any
$h^{2,0}(X)\gt 0$
. Fix any
![]() $\delta \in \mathbb{Z}$
such that
$\delta \in \mathbb{Z}$
such that
![]() $\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.5 implies that the coefficient of
$\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.5 implies that the coefficient of
![]() $q^{\delta /2r}$
in
$q^{\delta /2r}$
in
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
equals the coefficient of
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{Eu}}(q)$
equals the coefficient of
![]() $q^{\delta /2r}$
in
$q^{\delta /2r}$
in
 \begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i w} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
\begin{align*} & r^{2+K_X^2 - \chi (\mathcal{O}_X)} \Bigg ( {1 \over \overline{\Delta }(q^{\frac{1}{r}})^{\frac{1}{2}}} \Bigg )^{\chi (\mathcal{O}_X)} D_0^{K_X^2} \sum _{(a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}} \prod _{i} \epsilon _r^{i a_i w} \,{{\rm SW}}(a_i) \prod _{i \leq j} D_{ij}^{a_i a_j}. \end{align*}
Closed conjectural expressions for
![]() $D_0, D_{ij}$
can be found in [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b, Reference Göttsche, Kool and LaarakkerGKL24] for
$D_0, D_{ij}$
can be found in [Reference Göttsche and KoolGK18, Reference Göttsche and KoolGK20b, Reference Göttsche, Kool and LaarakkerGKL24] for
![]() $r=2,3,5$
. For
$r=2,3,5$
. For
![]() $r=2,3$
they are expressed in terms of the Dedekind eta function and the theta functions of the
$r=2,3$
they are expressed in terms of the Dedekind eta function and the theta functions of the
![]() $A_{r-1}^\vee$
lattice [Reference Göttsche and KoolGK19, Reference Göttsche and KoolGK20b]. For
$A_{r-1}^\vee$
lattice [Reference Göttsche and KoolGK19, Reference Göttsche and KoolGK20b]. For
![]() $r=5$
, the expressions also involve the Rogers–Ramanujan continued fraction [Reference Göttsche, Kool and LaarakkerGKL24].
$r=5$
, the expressions also involve the Rogers–Ramanujan continued fraction [Reference Göttsche, Kool and LaarakkerGKL24].
Let
![]() $X$
be a smooth projective surface satisfying
$X$
be a smooth projective surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
,
$H_1(X,\mathbb{Z}) = 0$
,
![]() $h^{2,0}(X)\gt 0$
, and let
$h^{2,0}(X)\gt 0$
, and let
![]() $c_1 \in H^2(X,\mathbb{Z})$
be an algebraic class. In [Reference Tanaka and ThomasTT20], Tanaka and Thomas give a mathematical definition of the
$c_1 \in H^2(X,\mathbb{Z})$
be an algebraic class. In [Reference Tanaka and ThomasTT20], Tanaka and Thomas give a mathematical definition of the
![]() ${\rm SU}(r)$
Vafa–Witten partition function
${\rm SU}(r)$
Vafa–Witten partition function
![]() $\mathsf{VW}^{{\rm SU}(r)}_{X,c_1}(q)$
. As mentioned in the introduction, for
$\mathsf{VW}^{{\rm SU}(r)}_{X,c_1}(q)$
. As mentioned in the introduction, for
![]() $r$
prime, a definition of the
$r$
prime, a definition of the
![]() ${\rm PSU}(r)$
Vafa–Witten partition function was given in [Reference Jiang and KoolJK21] (see also [Reference JiangJia22]). It is of the form
${\rm PSU}(r)$
Vafa–Witten partition function was given in [Reference Jiang and KoolJK21] (see also [Reference JiangJia22]). It is of the form
For
![]() $o(w)=0$
, one is reduced to untwisted Higgs pairs and
$o(w)=0$
, one is reduced to untwisted Higgs pairs and
![]() $\mathsf{VW}_{X,w}(q)$
can be defined using the approach of Tanaka and Thomas. For
$\mathsf{VW}_{X,w}(q)$
can be defined using the approach of Tanaka and Thomas. For
![]() $o(w) \neq 0$
, we take [Reference Jiang and KoolJK21]
$o(w) \neq 0$
, we take [Reference Jiang and KoolJK21]
Assuming the above-mentioned closed conjectural expressions for the universal functions for
![]() $r=2,3,5$
, the following
$r=2,3,5$
, the following
![]() $S$
-duality conjecture (due to Vafa and Witten [Reference Vafa and WittenVW94] and mathematically formulated in [Reference Jiang and KoolJK21]) was checked for
$S$
-duality conjecture (due to Vafa and Witten [Reference Vafa and WittenVW94] and mathematically formulated in [Reference Jiang and KoolJK21]) was checked for
![]() $r=2$
[Reference Dijkgraaf, Park and SchroersDPS99, Reference Göttsche and KoolGK18, Reference Vafa and WittenVW94],
$r=2$
[Reference Dijkgraaf, Park and SchroersDPS99, Reference Göttsche and KoolGK18, Reference Vafa and WittenVW94],
![]() $r=3$
[Reference Göttsche and KoolGK18] and
$r=3$
[Reference Göttsche and KoolGK18] and
![]() $r=5$
[Reference Göttsche, Kool and LaarakkerGKL24].
$r=5$
[Reference Göttsche, Kool and LaarakkerGKL24].
conjecture 5.7. (Vafa–Witten). Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
and
$H_1(X,\mathbb{Z}) = 0$
and
![]() $h^{2,0}(X)\gt 0$
. Let
$h^{2,0}(X)\gt 0$
. Let
![]() $r$
be prime and
$r$
be prime and
![]() $c_1 \in H^2(X,\mathbb{Z})$
algebraic. Then
$c_1 \in H^2(X,\mathbb{Z})$
algebraic. Then
![]() $\mathsf{VW}_{X,c_1}^{{\rm SU}(r)}(q)$
and
$\mathsf{VW}_{X,c_1}^{{\rm SU}(r)}(q)$
and
![]() $\mathsf{VW}_{X,c_1}^{{\rm PSU}(r)}(q)$
are Fourier expansions in
$\mathsf{VW}_{X,c_1}^{{\rm PSU}(r)}(q)$
are Fourier expansions in
![]() $q = \exp (2 \pi \sqrt{-1} \tau )$
of meromorphic functions
$q = \exp (2 \pi \sqrt{-1} \tau )$
of meromorphic functions
![]() $\mathsf{VW}_{X,c_1}^{{\rm SU}(r)}(\tau )$
and
$\mathsf{VW}_{X,c_1}^{{\rm SU}(r)}(\tau )$
and
![]() $\mathsf{VW}_{X,c_1}^{{\rm PSU}(r)}(\tau )$
on the upper half-plane satisfying
$\mathsf{VW}_{X,c_1}^{{\rm PSU}(r)}(\tau )$
on the upper half-plane satisfying
5.3 Application to
 $c_2^{{\rm min}}$
of Azumaya algebras
$c_2^{{\rm min}}$
of Azumaya algebras
Let
![]() $X$
be a smooth projective surface with
$X$
be a smooth projective surface with
![]() $H_1(X,\mathbb{Z}) = 0$
and function field
$H_1(X,\mathbb{Z}) = 0$
and function field
![]() $\mathbb{C}(X)$
. Let
$\mathbb{C}(X)$
. Let
![]() $D$
be a (central) division algebra over
$D$
be a (central) division algebra over
![]() $\mathbb{C}(X)$
of degree
$\mathbb{C}(X)$
of degree
![]() $r \gt 1$
(equivalently, an element of
$r \gt 1$
(equivalently, an element of
![]() ${\rm Br}(\mathbb{C}(X))$
of order
${\rm Br}(\mathbb{C}(X))$
of order
![]() $r$
). We assume
$r$
). We assume
![]() $D$
lies in the image of
$D$
lies in the image of
![]() ${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. As mentioned in the introduction, we are interested in the smallest
${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. As mentioned in the introduction, we are interested in the smallest
![]() $c_2$
for which there exists an Azumaya algebra
$c_2$
for which there exists an Azumaya algebra
![]() $\mathcal{A}$
on
$\mathcal{A}$
on
![]() $X$
whose stalk over the generic point
$X$
whose stalk over the generic point
![]() $\eta \in X$
is isomorphic to
$\eta \in X$
is isomorphic to
![]() $D$
. We refer to this value as
$D$
. We refer to this value as
![]() $c_2^{{\rm min}}$
and recall that Artin and de Jong proved [Reference Artin and de JongAdJ04, Corollary 7.1.5, Theorem 7.2.1]
$c_2^{{\rm min}}$
and recall that Artin and de Jong proved [Reference Artin and de JongAdJ04, Corollary 7.1.5, Theorem 7.2.1]
Our general strategy is as follows.
-
• Fix a class
 $w \in H^2(X,\mu _r)$
such that its Brauer class
$w \in H^2(X,\mu _r)$
such that its Brauer class
 $o(w) \in {\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
corresponds to
$o(w) \in {\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
corresponds to
 $D$
. This is possible since
$D$
. This is possible since
 $H^2(X,\mu _r)$
surjects onto
$H^2(X,\mu _r)$
surjects onto
 $H^2(X,\mathbb{G}_m)[r]$
by (5).
$H^2(X,\mathbb{G}_m)[r]$
by (5). -
• Fix any
 $\delta \in \mathbb{Z}$
such that
$\delta \in \mathbb{Z}$
such that
 $\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Suppose the coefficient of
$\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Suppose the coefficient of
 $q^{\delta /2r}$
of some
$q^{\delta /2r}$
of some
 ${\rm PGL}_r$
generating function
${\rm PGL}_r$
generating function
 $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r,\mathsf{P}}(q)$
is non-zero.
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r,\mathsf{P}}(q)$
is non-zero. -
• Denoting by
 $\xi \in H^2(X,\mathbb{Z})$
a lift of
$\xi \in H^2(X,\mathbb{Z})$
a lift of
 $w$
(Lemma 3.1), we conclude that for any degree
$w$
(Lemma 3.1), we conclude that for any degree
 $r$
Brauer–Severi variety
$r$
Brauer–Severi variety
 $Y \to X$
with
$Y \to X$
with
 $w(Y) = w$
(which exist by Theorem 2.16), the moduli space
$w(Y) = w$
(which exist by Theorem 2.16), the moduli space
 $M_{Y,\xi /r}^H(r,\xi, c_2)$
is non-empty, where
$M_{Y,\xi /r}^H(r,\xi, c_2)$
is non-empty, where
 $c_2 \in \mathbb{Z}$
is determined by the equation
$c_2 \in \mathbb{Z}$
is determined by the equation
 $\delta=2rc_2 - (r-1) \xi^2 - (r^2-1) \chi (\mathcal{O}_X)$
.
$\delta=2rc_2 - (r-1) \xi^2 - (r^2-1) \chi (\mathcal{O}_X)$
. -
• Therefore, by Corollary 3.9, there exists an Azumaya algebra
 $\mathcal{A}$
on
$\mathcal{A}$
on
 $X$
whose stalk over the generic point is isomorphic to
$X$
whose stalk over the generic point is isomorphic to
 $D$
satisfying
$D$
satisfying
 $c_2(\mathcal{A}) \leq \delta + (r^2-1) \chi (\mathcal{O}_X)$
. In particular
$c_2(\mathcal{A}) \leq \delta + (r^2-1) \chi (\mathcal{O}_X)$
. In particular
 $c_2^{{\rm min}} \leq \delta + (r^2-1) \chi (\mathcal{O}_X)$
.
$c_2^{{\rm min}} \leq \delta + (r^2-1) \chi (\mathcal{O}_X)$
.
We illustrate this strategy by focusing on the leading term of
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r,\mathsf{P}}(q)$
. For this, we use the explicit form of the Mariño–Moore conjecture [Reference Labastida and MariñoLM05, Reference Mariño and MooreMM98] due to Göttsche [Reference GöttscheGot21], which we now recall. For a smooth polarized surface
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r,\mathsf{P}}(q)$
. For this, we use the explicit form of the Mariño–Moore conjecture [Reference Labastida and MariñoLM05, Reference Mariño and MooreMM98] due to Göttsche [Reference GöttscheGot21], which we now recall. For a smooth polarized surface
![]() $(X,H)$
satisfying
$(X,H)$
satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
, we fix
$H_1(X,\mathbb{Z}) = 0$
, we fix
![]() $r,c_1$
so that there are no rank
$r,c_1$
so that there are no rank
![]() $r$
strictly Gieseker
$r$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with first Chern class
$X$
with first Chern class
![]() $c_1$
, and consider the Gieseker–Maruyama–Simpson moduli space
$c_1$
, and consider the Gieseker–Maruyama–Simpson moduli space
![]() $M_X^H(r,c_1,c_2)$
. For any class
$M_X^H(r,c_1,c_2)$
. For any class
![]() $\alpha \in H^*(X,\mathbb{Q})$
and
$\alpha \in H^*(X,\mathbb{Q})$
and
![]() $k \in \mathbb{Z}_{\geq 0}$
, one defines the
$k \in \mathbb{Z}_{\geq 0}$
, one defines the
![]() $\mu$
-insertion
$\mu$
-insertion
where
![]() $\pi _M, \pi _X$
are the projections from
$\pi _M, \pi _X$
are the projections from
![]() $M \times X$
to
$M \times X$
to
![]() $M,X$
respectively. Denote the Poincaré dual of the point class by
$M,X$
respectively. Denote the Poincaré dual of the point class by
![]() ${\rm pt} \in H^4(X,\mathbb{Z})$
. We are interested in the following generating series of (algebro-geometric)
${\rm pt} \in H^4(X,\mathbb{Z})$
. We are interested in the following generating series of (algebro-geometric)
![]() ${\rm SL}_r$
Donaldson invariants:
${\rm SL}_r$
Donaldson invariants:
where
![]() $L \in H^2(X,\mathbb{Z})$
and
$L \in H^2(X,\mathbb{Z})$
and
![]() $u$
is a formal variable. We first recall Witten’s conjecture, proved in the algebro-geometric set-up by Göttsche, Nakajima and Yoshioka [Reference Göttsche, Nakajima and YoshiokaGNY11].
$u$
is a formal variable. We first recall Witten’s conjecture, proved in the algebro-geometric set-up by Göttsche, Nakajima and Yoshioka [Reference Göttsche, Nakajima and YoshiokaGNY11].
Theorem 5.8. (Göttsche–Nakajima–Yoshioka). Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
and
$H_1(X,\mathbb{Z}) = 0$
and
![]() $h^{2,0}(X)\gt 0$
. Let
$h^{2,0}(X)\gt 0$
. Let
![]() $c_1 \in H^2(X,\mathbb{Z})$
be such that there are no rank
$c_1 \in H^2(X,\mathbb{Z})$
be such that there are no rank
![]() $2$
strictly Gieseker
$2$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with first Chern class
$X$
with first Chern class
![]() $c_1$
. Then the coefficient of
$c_1$
. Then the coefficient of
![]() $z^{{\rm vd}(2,c_1,c_2)}$
in
$z^{{\rm vd}(2,c_1,c_2)}$
in
![]() $\mathsf{Z}_{(X,H),c_1}^{{\rm SL}_2,\mathsf{D}}(z)$
equals the coefficient of
$\mathsf{Z}_{(X,H),c_1}^{{\rm SL}_2,\mathsf{D}}(z)$
equals the coefficient of
![]() $z^{{\rm vd}(2,c_1,c_2)}$
in
$z^{{\rm vd}(2,c_1,c_2)}$
in
The higher rank generalization of Witten’s conjecture is known as the Mariño–Moore conjecture [Reference Mariño and MooreMM98] (see also [Reference Labastida and MariñoLM05]). We discuss its algebro-geometric version due to Göttsche [Reference GöttscheGot21]. Define
![]() $[r-1] := \{1, \ldots, r-1\}$
. We require the following numbers: for all
$[r-1] := \{1, \ldots, r-1\}$
. We require the following numbers: for all
![]() $1 \leq i \lt j \leq r-1$
,
$1 \leq i \lt j \leq r-1$
,
 \begin{align*} \beta _{ij} & := {\sin ((i+j)\pi / 2r) \over \sin ((j-i)\pi / 2r)} \in \mathbb{R}_{\gt 0}, \quad \beta _{ji} := \beta _{ij}, \\ B & := \sum _{I \subset [r-1]} \prod _{i \in I \atop j \in [r-1] \setminus I} \beta _{ij}. \end{align*}
\begin{align*} \beta _{ij} & := {\sin ((i+j)\pi / 2r) \over \sin ((j-i)\pi / 2r)} \in \mathbb{R}_{\gt 0}, \quad \beta _{ji} := \beta _{ij}, \\ B & := \sum _{I \subset [r-1]} \prod _{i \in I \atop j \in [r-1] \setminus I} \beta _{ij}. \end{align*}
Conjecture 5.9. (Göttsche). Let
![]() $(X,H)$
be a smooth polarized surface satisfying
$(X,H)$
be a smooth polarized surface satisfying
![]() $H_1(X,\mathbb{Z}) = 0$
and
$H_1(X,\mathbb{Z}) = 0$
and
![]() $h^{2,0}(X)\gt 0$
. Let
$h^{2,0}(X)\gt 0$
. Let
![]() $r\gt 1$
and
$r\gt 1$
and
![]() $c_1 \in H^2(X,\mathbb{Z})$
such that there are no rank
$c_1 \in H^2(X,\mathbb{Z})$
such that there are no rank
![]() $r$
strictly Gieseker
$r$
strictly Gieseker
![]() $H$
-semistable sheaves on
$H$
-semistable sheaves on
![]() $X$
with first Chern class
$X$
with first Chern class
![]() $c_1$
. Then the coefficient of
$c_1$
. Then the coefficient of
![]() $z^{{\rm vd}(r,c_1,c_2)}$
in
$z^{{\rm vd}(r,c_1,c_2)}$
in
![]() $\mathsf{Z}_{(X,H),c_1}^{{\rm SL}_r,\mathsf{D}}(z)$
equals the coefficient of
$\mathsf{Z}_{(X,H),c_1}^{{\rm SL}_r,\mathsf{D}}(z)$
equals the coefficient of
![]() $z^{{\rm vd}(r,c_1,c_2)}$
in
$z^{{\rm vd}(r,c_1,c_2)}$
in
where the sum is over all
![]() $\boldsymbol{a} = (a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}$
.
$\boldsymbol{a} = (a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}$
.
The
![]() $r=3,4,5$
cases of this conjecture also appear in [Reference Göttsche and KoolGK22, Reference Göttsche, Kool and LaarakkerGKL24] as consequences of other conjectures.
$r=3,4,5$
cases of this conjecture also appear in [Reference Göttsche and KoolGK22, Reference Göttsche, Kool and LaarakkerGKL24] as consequences of other conjectures.
Let
![]() $w \in H^2(X,\mu _r)$
,
$w \in H^2(X,\mu _r)$
,
![]() $\pi : Y \to X$
a choice of degree
$\pi : Y \to X$
a choice of degree
![]() $r$
Brauer–Severi variety with
$r$
Brauer–Severi variety with
![]() $w(Y)=w$
(Theorem 2.16), and
$w(Y)=w$
(Theorem 2.16), and
![]() $\xi \in H^2(X,\mathbb{Z})$
a lift of
$\xi \in H^2(X,\mathbb{Z})$
a lift of
![]() $w$
(Lemma 3.1). We assume
$w$
(Lemma 3.1). We assume
![]() $r$
is prime and
$r$
is prime and
![]() ${\rm gcd}(r,wH)=1$
. We consider the following generating series of
${\rm gcd}(r,wH)=1$
. We consider the following generating series of
![]() ${\rm PGL}_r$
Donaldson invariants:
${\rm PGL}_r$
Donaldson invariants:
where, for any
![]() $\alpha \in H^*(X,\mathbb{Q})$
, we define
$\alpha \in H^*(X,\mathbb{Q})$
, we define
Corollary 5.10.
Suppose
![]() $X = \mathcal{X}_0$
and
$X = \mathcal{X}_0$
and
![]() $w = \widetilde{w}_0$
for a family
$w = \widetilde{w}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4 and
$\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4 and
![]() $h^{2,0}(X)\gt 0$
. Fix any
$h^{2,0}(X)\gt 0$
. Fix any
![]() $\delta \in \mathbb{Z}$
such that
$\delta \in \mathbb{Z}$
such that
![]() $\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.9 (which holds for
$\delta \equiv -(r-1) w^2 - (r^2-1) \chi (\mathcal{O}_X) \mod 2r$
. Then Conjecture 5.9 (which holds for
![]() $r=2$
) implies that the coefficient of
$r=2$
) implies that the coefficient of
![]() $z^{\delta }$
in
$z^{\delta }$
in
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{D}}(z)$
equals the coefficient of
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{D}}(z)$
equals the coefficient of
![]() $z^{\delta }$
in
$z^{\delta }$
in
where the sum is over all
![]() $\boldsymbol{a} = (a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}$
.
$\boldsymbol{a} = (a_1, \ldots, a_{r-1}) \in H^2(X,\mathbb{Z})^{r-1}$
.
Suppose
![]() $X$
is a minimal surface of general type satisfying
$X$
is a minimal surface of general type satisfying
![]() $H_1(X,\mathbb{Z})=0$
and
$H_1(X,\mathbb{Z})=0$
and
![]() $h^{2,0}(X)\gt 0$
. Then the only Seiberg–Witten basic classes
$h^{2,0}(X)\gt 0$
. Then the only Seiberg–Witten basic classes
![]() $a \in H^2(X,\mathbb{Z})$
, i.e. the only classes for which
$a \in H^2(X,\mathbb{Z})$
, i.e. the only classes for which
![]() ${\rm SW}(a) \neq 0$
, are
${\rm SW}(a) \neq 0$
, are
![]() $a=0,K_X$
and the corresponding Seiberg–Witten invariants are
$a=0,K_X$
and the corresponding Seiberg–Witten invariants are
![]() $1, (-1)^{\chi (\mathcal{O}_X)}$
[Reference MorganMor96, Theorem 7.4.1]. Then the formula of Corollary 5.10 simplifies dramatically. We take
$1, (-1)^{\chi (\mathcal{O}_X)}$
[Reference MorganMor96, Theorem 7.4.1]. Then the formula of Corollary 5.10 simplifies dramatically. We take
![]() $u=0$
and
$u=0$
and
![]() $L=K_X$
and record the leading coefficients of the formula for
$L=K_X$
and record the leading coefficients of the formula for
![]() $r=2,3$
. The main observation is that in each case the leading coefficient is positive.
$r=2,3$
. The main observation is that in each case the leading coefficient is positive.
Example 5.11. For
![]() $r=2$
, we have the following cases.
$r=2$
, we have the following cases.
-
• For
 $w K_X + \chi (\mathcal{O}_X) \equiv 0 \mod 2$
, the leading term isTaking a representative
$w K_X + \chi (\mathcal{O}_X) \equiv 0 \mod 2$
, the leading term isTaking a representative \begin{align*}2^{2 - \chi (\mathcal {O}_X) + K_X^2} \cdot 2 z^0. \end{align*}
\begin{align*}2^{2 - \chi (\mathcal {O}_X) + K_X^2} \cdot 2 z^0. \end{align*}
 $w = [\xi ]$
with
$w = [\xi ]$
with
 $\xi \in H^2(X,\mathbb{Z})$
, in this case we have
$\xi \in H^2(X,\mathbb{Z})$
, in this case we have
 ${\rm vd}(2,w,c_2) \equiv 0 \mod 2$
for all
${\rm vd}(2,w,c_2) \equiv 0 \mod 2$
for all
 $c_2 \in \mathbb{Z}$
. Here we used Wu’s formula
$c_2 \in \mathbb{Z}$
. Here we used Wu’s formula
 $w^2 \equiv w K_X \mod 2$
.
$w^2 \equiv w K_X \mod 2$
.
-
• For
 $w K_X + \chi (\mathcal{O}_X) \equiv 1 \mod 2$
, the leading term isTaking a representative
$w K_X + \chi (\mathcal{O}_X) \equiv 1 \mod 2$
, the leading term isTaking a representative \begin{align*}2^{2 - \chi (\mathcal {O}_X) + K_X^2} (2K_X^2) z.\end{align*}
\begin{align*}2^{2 - \chi (\mathcal {O}_X) + K_X^2} (2K_X^2) z.\end{align*}
 $w = [\xi ]$
with
$w = [\xi ]$
with
 $\xi \in H^2(X,\mathbb{Z})$
, in this case we have
$\xi \in H^2(X,\mathbb{Z})$
, in this case we have
 ${\rm vd}(2,w,c_2) \equiv 1 \mod 2$
for all
${\rm vd}(2,w,c_2) \equiv 1 \mod 2$
for all
 $c_2 \in \mathbb{Z}$
.
$c_2 \in \mathbb{Z}$
.
Example 5.12. For
![]() $r=3$
, we have the following cases.
$r=3$
, we have the following cases.
-
• For
 $w K_X \equiv 0 \mod 3$
,
$w K_X \equiv 0 \mod 3$
,
 $\chi (\mathcal{O}_X) \equiv 0 \mod 2$
the leading term is
$\chi (\mathcal{O}_X) \equiv 0 \mod 2$
the leading term is \begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}+2) z^0.\end{align*}
\begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}+2) z^0.\end{align*}
-
• For
 $w K_X \equiv 0 \mod 3$
,
$w K_X \equiv 0 \mod 3$
,
 $\chi (\mathcal{O}_X) \equiv 1 \mod 2$
the leading term is
$\chi (\mathcal{O}_X) \equiv 1 \mod 2$
the leading term is \begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}-2) z^0.\end{align*}
\begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}-2) z^0.\end{align*}
-
• For
 $w K_X \equiv 1,2 \mod 3$
,
$w K_X \equiv 1,2 \mod 3$
,
 $\chi (\mathcal{O}_X) \equiv 0 \mod 2$
the leading term is
$\chi (\mathcal{O}_X) \equiv 0 \mod 2$
the leading term is \begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}-1) z^0.\end{align*}
\begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}-1) z^0.\end{align*}
-
• For
 $w K_X \equiv 1,2 \mod 3$
,
$w K_X \equiv 1,2 \mod 3$
,
 $\chi (\mathcal{O}_X) \equiv 1 \mod 2$
the leading term is
$\chi (\mathcal{O}_X) \equiv 1 \mod 2$
the leading term is \begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}+1) z^0.\end{align*}
\begin{align*}3^{2-\chi (\mathcal {O}_X) + K_X^2}(2^{1+K_X^2}+1) z^0.\end{align*}
Taking a representative
![]() $w = [\xi ]$
with
$w = [\xi ]$
with
![]() $\xi \in H^2(X,\mathbb{Z})$
, in each of these cases we have
$\xi \in H^2(X,\mathbb{Z})$
, in each of these cases we have
![]() ${\rm vd}(r,\xi, c_2) \equiv 0 \mod 2$
for any
${\rm vd}(r,\xi, c_2) \equiv 0 \mod 2$
for any
![]() $c_2 \in \mathbb{Z}$
.
$c_2 \in \mathbb{Z}$
.
Remark 5.13. It is natural to expect that the formula for
![]() $\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{D}}$
of Corollary 5.10 also holds when
$\mathsf{Z}_{(X,H),w}^{{\rm PGL}_r, \mathsf{D}}$
of Corollary 5.10 also holds when
![]() $r\gt 1$
is not necessarily prime (at least when there are no strictly semistables). Experimentation for ranks
$r\gt 1$
is not necessarily prime (at least when there are no strictly semistables). Experimentation for ranks
![]() $r\gt 3$
leads us to the following expectations. For
$r\gt 3$
leads us to the following expectations. For
![]() $X,H,w$
as above and any odd rank
$X,H,w$
as above and any odd rank
![]() $r$
, we have
$r$
, we have
Moreover, for any even rank
![]() $r$
, we have
$r$
, we have
 \begin{align*} \left \{ \begin {array}{c@{\quad}c} \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {D}}(0) \in \mathbb {Z}_{\gt 0} & \mathrm {if \ } wK_X + \chi (\mathcal {O}_X) \equiv 0 \mod 2, \\[8pt] \frac {\partial }{\partial z} \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {D}}(0) \in \mathbb {Z}_{\gt 0} & \mathrm {if \ } wK_X + \chi (\mathcal {O}_X) \equiv 1 \mod 2. \end {array} \right . \end{align*}
\begin{align*} \left \{ \begin {array}{c@{\quad}c} \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {D}}(0) \in \mathbb {Z}_{\gt 0} & \mathrm {if \ } wK_X + \chi (\mathcal {O}_X) \equiv 0 \mod 2, \\[8pt] \frac {\partial }{\partial z} \mathsf {Z}_{(X,H),w}^{\mathrm {PGL}_r, \mathsf {D}}(0) \in \mathbb {Z}_{\gt 0} & \mathrm {if \ } wK_X + \chi (\mathcal {O}_X) \equiv 1 \mod 2. \end {array} \right . \end{align*}
Taking a representative
![]() $w = [\xi ]$
with
$w = [\xi ]$
with
![]() $\xi \in H^2(X,\mathbb{Z})$
, for
$\xi \in H^2(X,\mathbb{Z})$
, for
![]() $r$
odd we have
$r$
odd we have
![]() ${\rm vd}(r,\xi, c_2) \equiv 0 \mod 2$
, and for
${\rm vd}(r,\xi, c_2) \equiv 0 \mod 2$
, and for
![]() $r$
even we have
$r$
even we have
![]() ${\rm vd}(r,\xi, c_2) \equiv w K_X + \chi (\mathcal{O}_X) \mod 2$
for any
${\rm vd}(r,\xi, c_2) \equiv w K_X + \chi (\mathcal{O}_X) \mod 2$
for any
![]() $c_2 \in \mathbb{Z}$
. This positivity is obvious in the case
$c_2 \in \mathbb{Z}$
. This positivity is obvious in the case
![]() $r$
is odd,
$r$
is odd,
![]() $wK_X \equiv 0 \mod r$
, and
$wK_X \equiv 0 \mod r$
, and
![]() $\chi (\mathcal{O}_X) \equiv 0 \mod 2$
, but appears non-trivial in general.Footnote
25
$\chi (\mathcal{O}_X) \equiv 0 \mod 2$
, but appears non-trivial in general.Footnote
25
Combining Example 5.11 and Corollary 5.10, we deduce the following.
Theorem 5.14.
Suppose
![]() $X = \mathcal{X}_0$
for a family
$X = \mathcal{X}_0$
for a family
![]() $\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4
, and
$\mathcal{X} \to B$
satisfying the conditions of Theorem 5.4
, and
![]() $X$
is a minimal surface of general type satisfying
$X$
is a minimal surface of general type satisfying
![]() $h^{2,0}(X)\gt 0$
. Let
$h^{2,0}(X)\gt 0$
. Let
![]() $D \in {\rm Br}(\mathbb{C}(X))$
be a degree
$D \in {\rm Br}(\mathbb{C}(X))$
be a degree
![]() $r$
division algebra in the image of
$r$
division algebra in the image of
![]() ${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. Then, for
${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
. Then, for
![]() $r=2$
, we have
$r=2$
, we have
Moreover, for
![]() $r=3$
and assuming Göttsche’s conjecture 5.9 for
$r=3$
and assuming Göttsche’s conjecture 5.9 for
![]() $r=3$
, we have
$r=3$
, we have
Proof.
Let
![]() $\alpha \in {\rm Br}(X)$
be the Brauer class corresponding to
$\alpha \in {\rm Br}(X)$
be the Brauer class corresponding to
![]() $D$
. Let
$D$
. Let
![]() $Y$
be a degree
$Y$
be a degree
![]() $r$
Brauer–Severi variety with
$r$
Brauer–Severi variety with
![]() $o(w(Y)) = \alpha$
(Theorem 2.16).
$o(w(Y)) = \alpha$
(Theorem 2.16).
For
![]() $r=2$
, by Example 5.11, there are two cases. (1) For
$r=2$
, by Example 5.11, there are two cases. (1) For
![]() $w K_X + \chi (\mathcal{O}_X) \equiv 0 \mod 2$
and running the strategy at the beginning of this section, we deduce
$w K_X + \chi (\mathcal{O}_X) \equiv 0 \mod 2$
and running the strategy at the beginning of this section, we deduce
![]() $c_2^{{\rm min}} \leq 3\chi (\mathcal{O}_X)$
. (2) For
$c_2^{{\rm min}} \leq 3\chi (\mathcal{O}_X)$
. (2) For
![]() $w K_X + \chi (\mathcal{O}_X) \equiv 1 \mod 2$
, we deduce
$w K_X + \chi (\mathcal{O}_X) \equiv 1 \mod 2$
, we deduce
![]() $c_2^{{\rm min}} \leq 3\chi (\mathcal{O}_X)+1$
.
$c_2^{{\rm min}} \leq 3\chi (\mathcal{O}_X)+1$
.
For
![]() $r=3$
, Example 5.11 implies the result.
$r=3$
, Example 5.11 implies the result.
In general, if the expectation of Remark 5.13 holds and we take
![]() $X$
as in the previous theorem, then for any degree
$X$
as in the previous theorem, then for any degree
![]() $r\gt 1$
division algebra
$r\gt 1$
division algebra
![]() $D \in {\rm Br}(\mathbb{C}(X))$
in the image of
$D \in {\rm Br}(\mathbb{C}(X))$
in the image of
![]() ${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
, we obtain
${\rm Br}(X) \hookrightarrow {\rm Br}(\mathbb{C}(X))$
, we obtain
 \begin{align*} \begin{cases}c_2^{{\rm min}} \leq (r^2-1)\chi (\mathcal{O}_X)+1 & \textrm{for } r \textrm{ even}, \\ c_2^{{\rm min}} \leq (r^2-1)\chi (\mathcal{O}_X) & \textrm{for } r \textrm{ odd}. \end{cases}\end{align*}
\begin{align*} \begin{cases}c_2^{{\rm min}} \leq (r^2-1)\chi (\mathcal{O}_X)+1 & \textrm{for } r \textrm{ even}, \\ c_2^{{\rm min}} \leq (r^2-1)\chi (\mathcal{O}_X) & \textrm{for } r \textrm{ odd}. \end{cases}\end{align*}
Acknowledgements
The authors express their gratitude to Y. Bae, P. Brosnan, H. Movasati, G. Oberdieck, H. Park, C.A.M. Peters, F. Reede, R.P. Thomas and Q. Yin for useful discussions. M.K. would like to provide special thanks to L. Göttsche, since this paper grew out of an attempt to find a geometric motivation for [Reference Göttsche and KoolGK18, Remark 1.9] (see also [Reference Göttsche, Kool and LaarakkerGKL24, §4.3]) in their collaboration.
Conflicts of Interest
None.
Financial Support
D.vB. and M.K. are supported by NWO grant VI.Vidi.192.012. M.K. is also supported by ERC Consolidator Grant FourSurf 101087365. A.G. and Y.J. are supported by Simons Foundation Collaboration Grants for Mathematicians and Y.J. is also supported by a KU Research GO grant from the University of Kansas.
Journal Information
Moduli is published as a joint venture of the Foundation Compositio Mathematica and the London Mathematical Society. As not-for-profit organisations, the Foundation and Society reinvest
![]() $100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.
$100\%$
of any surplus generated from their publications back into mathematics through their charitable activities.