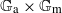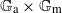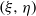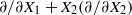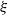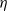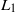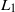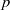Research Article
INTERMEDIATE SUMS ON POLYHEDRA: COMPUTATION AND REAL EHRHART THEORY
- Part of:
-
- Published online by Cambridge University Press:
- 05 September 2012, pp. 1-22
-
- Article
- Export citation
KAKEYA SETS OVER NON-ARCHIMEDEAN LOCAL RINGS
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 257-266
-
- Article
- Export citation
ALMOST ALL SETS OF
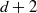 $d+ 2$ POINTS ON THE
$d+ 2$ POINTS ON THE 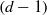 $(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
$(d- 1)$-SPHERE ARE NOT SUBTRANSITIVE
- Part of:
-
- Published online by Cambridge University Press:
- 28 March 2013, pp. 267-268
-
- Article
- Export citation
ON A STRONG VERSION OF THE KEPLER CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 01 August 2012, pp. 23-30
-
- Article
-
- You have access
- Export citation
ON MULTIPLICATIVELY BADLY APPROXIMABLE NUMBERS
- Part of:
-
- Published online by Cambridge University Press:
- 12 June 2012, pp. 31-55
-
- Article
- Export citation
DISSOLVING OF CUSP FORMS: HIGHER-ORDER FERMI’S GOLDEN RULES
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 269-301
-
- Article
- Export citation
A NOTE ON THE HAUSDORFF DIMENSION OF SOME LIMINF SETS APPEARING IN SIMULTANEOUS DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 56-64
-
- Article
- Export citation
ON SELMER GROUPS OF QUADRATIC TWISTS OF ELLIPTIC CURVES WITH A TWO-TORSION OVER
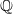 $\mathbb {Q}$
$\mathbb {Q}$
- Part of:
-
- Published online by Cambridge University Press:
- 15 January 2013, pp. 303-319
-
- Article
- Export citation
ZERO-ONE LAWS IN SIMULTANEOUS AND MULTIPLICATIVE DIOPHANTINE APPROXIMATION
- Part of:
-
- Published online by Cambridge University Press:
- 21 January 2013, pp. 321-332
-
- Article
- Export citation
ON THE DIOPHANTINE PROPERTIES OF λ-EXPANSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2012, pp. 65-86
-
- Article
- Export citation
THE RESONANCE METHOD FOR LARGE CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 11 September 2012, pp. 87-118
-
- Article
- Export citation
A SMALL VALUE ESTIMATE FOR
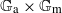 $\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
$\mathbb {G}_{{\textrm{a}}}\times \mathbb {G}_{{\textrm{m}}}$
- Part of:
-
- Published online by Cambridge University Press:
- 01 February 2013, pp. 333-363
-
- Article
- Export citation
LOWER BOUNDS FOR
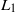 ${L}_{1} $ DISCREPANCY
${L}_{1} $ DISCREPANCY
- Part of:
-
- Published online by Cambridge University Press:
- 18 March 2013, pp. 365-379
-
- Article
- Export citation
CONTINUOUS LOWER BOUNDS FOR MOMENTS OF ZETA AND L-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 15 November 2012, pp. 119-128
-
- Article
- Export citation
THE VALUE DISTRIBUTION OF INCOMPLETE GAUSS SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 19 February 2013, pp. 381-398
-
- Article
- Export citation
THE MONTGOMERY–HOOLEY THEOREM IN SHORT INTERVALS
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 129-139
-
- Article
- Export citation
SINGULAR SCHRÖDINGER OPERATORS IN ONE DIMENSION
- Part of:
-
- Published online by Cambridge University Press:
- 12 April 2012, pp. 141-159
-
- Article
- Export citation
ON A CONJECTURE OF IGUSA
- Part of:
-
- Published online by Cambridge University Press:
- 07 February 2013, pp. 399-425
-
- Article
- Export citation
L1-SMOOTHING FOR THE ORNSTEIN–UHLENBECK SEMIGROUP
- Part of:
-
- Published online by Cambridge University Press:
- 02 August 2012, pp. 160-168
-
- Article
- Export citation
THE DISTRIBUTION OF THE MAXIMUM OF CHARACTER SUMS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2013, pp. 427-442
-
- Article
- Export citation

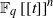
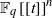
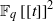
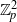
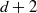
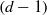
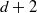
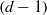
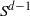
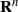
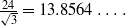
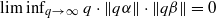 for all (
for all (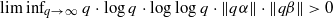 is of full dimension.
is of full dimension.
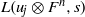
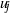
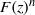
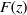
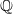
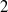
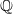
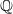
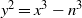
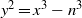
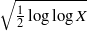
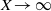
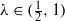 and
and 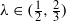 , the upper bound of
, the upper bound of